2015 Detailed List of Lecture Topics
(Quantum Theory for Computer Age {QTCA} - Ch. 1 of Unit 1)
(Principles of Symmetry, Dynamics, and Spectroscopy {PSDS} - Sec. 1-2 of Ch. 1)
Beam Sorters
2-State Sorters: spin-1/2 vs. optical polarization
Geometry of optical polarization selection and Brewster’s angle
Feynman’s lever
Beam Sorters in Series and Transformation Matrices
Introducing Dirac bra-ket notation
“Abstraction” of bra and ket vectors from a Transformation Matrix
Introducing scalar and matrix products
Textbooks (Online!)
Link → Quantum Theory for the Computer Age
URL is http://www.uark.edu/ua/modphys/markup/QTCAWeb.html
Link → Principles of Symmetry, Dynamics, and Spectroscopy
URL is http://www.uark.edu/ua/modphys/markup/PSDSWeb.html
(Quantum Theory for Computer Age - Ch. 1 of Unit 1 )
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-2 of Ch. 1 )
Review:“Abstraction” of bra and ket vectors from a Transformation Matrix
Introducing scalar and matrix products
Planck's energy and N-quanta (Cavity/Beam wave mode)
Did Max Planck Goof? What’s 1-photon worth?
Feynman amplitude axiom 1
What comes out of a beam sorter channel or branch-b?
Sample calculations
Feynman amplitude axioms 2-3
Beam analyzers: Sorter-unsorters
The “Do-Nothing” analyzer
Feynman amplitude axiom 4
Some “Do-Something” analyzers
Sorter-counter, Filter, 1/2-wave plate, 1/4-wave plate
From the Quantum Theory in the Computer Age:
Link → http://www.uark.edu/ua/modphys/pdfs/QTCA_Pdfs/QTCA_Text_2013/QTCA_Unit_1_Ch._1_2013.pdf
Link → http://www.uark.edu/ua/modphys/pdfs/QTCA_Pdfs/QTCA_Text_2013/QTCA_Unit_7_Ch._22_2005.pdf
See also the 2005 Pirelli Challenge site:
Link → http://www.uark.edu/ua/pirelli/php/light_energy_flux_1.php
Link → http://www.uark.edu/ua/pirelli/php/amplitude_probability_1.php
(Quantum Theory for Computer Age - Ch. 1-2 of Unit 1 )
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-3 of Ch. 1 )
Review: Axioms 1-4 and“Do-Nothing”vs“ Do-Something” analyzers
Abstraction of Axiom-4 to define projection and unitary operators
Projection operators and resolution of identity
Unitary operators and matrices that do something (or “nothing”)
Diagonal unitary operators
Non-diagonal unitary operators and †-conjugation relations
Non-diagonal projection operators and Kronecker ⊗-products
Axiom-4 similarity transformation
Matrix representation of beam analyzers
Non-unitary “killer” devices: Sorter-counter, filter
Unitary “non-killer” devices: 1/2-wave plate, 1/4-wave plate
How analyzers “peek” and how that changes outcomes
Peeking polarizers and coherence loss
Classical Bayesian probability vs. Quantum probability
Feynman 〈j⏐k〉-axioms compared to Group axioms
(Quantum Theory for Computer Age - Ch. 3 of Unit 1 )
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-3 of Ch. 1 )
Unitary operators and matrices that change state vectors
... and eigenstates (“ownstates) that are mostly immune
Geometric visualization of real symmetric matrices and eigenvectors
Circle-to-ellipse mapping (and I’m Ba-aaack!)
Ellipse-to-ellipse mapping (Normal space vs. tangent space)
Eigensolutions as stationary extreme-values (Lagrange λ-multipliers)
Matrix-algebraic eigensolutions with example M =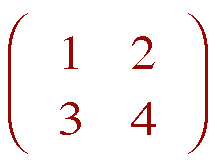 
Secular equation
Hamilton-Cayley equation and projectors
Idempotent projectors (how eigenvalues⇒eigenvectors)
Operator orthonormality and completeness
Spectral Decompositions
Functional spectral decomposition
Orthonormality vs. Completeness vis-a`-vis Operator vs. State
Lagrange functional interpolation formula
Proof that completeness relation is “Truer-than-true”
Diagonalizing Transformations (D-Ttran) from projectors
Eigensolutions for active analyzers
(Quantum Theory for Computer Age - Ch. 3 of Unit 1)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-3 of Ch. 1)
Review: matrix eigenstates (“ownstates) and Idempotent projectors (Non-degeneracy case)
Operator orthonormality, completeness, and spectral decomposition(Non-degenerate e-values)
(Preparing for: Degenerate eigenvalues)
Eigensolutions with degenerate eigenvalues (Possible?... or not?)
Secular → Hamilton-Cayley → Minimal equations
Diagonalizability criterion
Nilpotents and “Bad degeneracy” examples: B =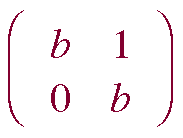 
, and: N =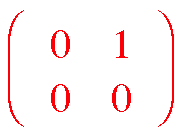 
Applications of Nilpotent operators later on
Idempotents and “Good degeneracy” example: G =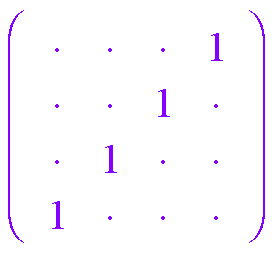 
Secular equation by minor expansion
Example of minimal equation projection
Orthonormalization of degenerate eigensolutions
Projection Pj-matrix anatomy (Gramian matrices)
Gram-Schmidt procedure
Orthonormalization of commuting eigensolutions. Examples: G = and: H = 
The old "1 = 1∙1 trick" - Spectral decomposition by projector splitting
Irreducible projectors and representations (Trace checks)
Minimal equation for projector P = P2
How symmetry groups become eigen-solvers
(Quantum Theory for Computer Age - Ch. 7-9 of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-3 of Ch. 2)
Review:How symmetry groups become eigen-solvers
How C2 (Bilateral σB reflection) symmetry is eigen-solver
C2 Symmetric two-dimensional harmonic oscillators (2DHO)
C2 (Bilateral σB reflection) symmetry conditions:
Minimal equation of σB and spectral decomposition of C2(σB)
C2 Symmetric 2DHO eigensolutions
C2 Mode phase character table
C2 Symmetric 2DHO uncoupling and mixed mode projector algebra
2D-HO beats and mixed mode geometry
Three famous 2-state systems and two-complex-component coordinates
ANALOGY: U(2) vs R(3): 2-State Schrodinger: iħ∂t|Ψ(t)〉= H|Ψ(t)〉 vs. Classical 2D-HO: ∂2tx=-K•x
Hamilton-Pauli spinor symmetry ( σ-expansion in ABCD-Types) H = ωμσμ
(Quantum Theory for Computer Age - Ch. 10 of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-3 of Ch. 5)
Review of Lecture 6: 2 symmetry is 2D oscillators and three famous 2-state systems
Review of Lecture 6: 2-State Schrodinger: iħ∂t|Ψ(t)〉= H|Ψ(t)〉 vs. Classical 2D-HO: ∂2tx=-K•x
Review of Lecture 6: Hamilton-Pauli spinor symmetry ( σ-expansion in ABCD-Types) H = ωμσμ
Derive σ-exponential time evolution (or revolution) operator U = e-iHt = e-iσµωµt
Spinor arithmetic like complex arithmetic
Spinor vector algebra like complex vector algebra
Spinor exponentials like complex exponentials (“Crazy-Thing”-Theorem)
Geometry of U(2) evolution (or R(3) revolution) operator U = e-iHt = e-iσμωμt
The “mysterious” factors of 2 (or 1/2): 2D Spinor vs 3D Spin Vector space
2D Spinor vs 3D vector rotation
NMR Hamiltonian: 3D Spin Moment m in B field
Euler’s state definition using rotations R(α,0,0), R(0,β,0), and R(0,0,γ)
Spin-1 (3D-real vector) case
Spin-1/2 (2D-complex spinor) case
3D-real Stokes Vector defines 2D-HO polarization ellipses and spinor states
Asymmetry SA = SZ, Balance SB = SX, and Chirality SC = SY
Polarization ellipse and spinor state dynamics
(Quantum Theory for Computer Age - Ch. 10A-B of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-3 of Ch. 5)
Review: How the “Crazy-Thing”-Theorem makes spinor and vector representation matrices
Half-angle Θ/2 = ϕ replacement and Darboux crank axis operators
Operator-on-Operator transformations
Product algebra for Pauli's σμ and Hamilton's qμ = -iσμ
Group product algebra
Jordan-Pauli identity and U(2) product R[Θ]R[Θ′]=R[Θ′′′] - formula
Transformation R[Θ]σμR[Θ]† of spinor σμ-operators
Transformation R[Θ]R[Θ′]R[Θ]† of group-operators
Operator-on-Operator transformations
Geometry of groups: Hamilton’s turns and It’s all done with mirrors!
Group product geometry
U(2) product R[Θ]R[Θ′] - geometry
Transformation R[Θ]R[Θ′]R[Θ]† geometry
Euler R(αβγ) versus Darboux R[ϕϑΘ]
Euler R(αβγ) related to Darboux R[ϕϑΘ]
Euler R(αβγ) rotation Θ =0-4π-sequence [ϕϑ] fixed
R(3)-U(2) slide rule for converting R(αβγ) ↔ R[ϕϑΘ]
Euler R(αβγ) Sundial
(Quantum Theory for Computer Age - Ch. 10A-B of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-3 of Ch. 5 and Ch. 7)
Review: Fundamental Euler R(αβγ) and Darboux R[ϕϑΘ] representations of U(2) and R(3)
Euler R(αβγ) derived from Darboux R[ϕϑΘ] and vice versa
Euler R(αβγ) rotation Θ =0-4π-sequence [ϕϑ] fixed (and “real-world” applications)
R(3)-U(2) slide rule for converting R(αβγ) ↔ R[ϕϑΘ] and Sundial
(Quantum Theory for Computer Age - Ch. 10A-B of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-3 of Ch. 5 and Ch. 7)
Review: Fundamental Euler R(αβγ) and Darboux R[ϕϑΘ] representations of U(2) and R(3)
Euler R(αβγ) derived from Darboux R[ϕϑΘ] and vice versa
Euler R(αβγ) rotation Θ =0-4π-sequence [ϕϑ] fixed (and “real-world” applications)
U(2) density operator approach to symmetry dynamics
Bloch equation for density operator
Quick U(2) way to find eigen-solutions for 2-by-2 H
The ABC’s of U(2) dynamics-Archetypes
Asymmetric-Diagonal A-Type motion
Bilateral-Balanced B-Type motion
Circular-Coriolis… C-Type motion
The ABC’s of U(2) dynamics-Mixed modes
AB-Type motion and Wigner’s Avoided-Symmetry-Crossings
ABC-Type elliptical polarized motion
Ellipsometry using U(2) symmetry coordinates
Conventional amp-phase ellipse coordinates
Euler Angle (αβγ) ellipse coordinates
(Quantum Theory for Computer Age - Ch. 6-9 of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 3-7 of Ch. 2)
Review of C2 spectral resolution for 2D oscillator (Lecture 6 : p. 11, p. 17, and p. 11)
C3 g†g-product-table and basic group representation theory
C3 H-and-rp-matrix representations and conjugation symmetry
C3 Spectral resolution: 3rd roots of unity and ortho-completeness relations
C3 character table and modular labeling
Ortho-completeness inversion for operators and states
Comparing wave function operator algebra to bra-ket algebra
Modular quantum number arithmetic
C3-group jargon and structure of various tables
C3 Eigenvalues and wave dispersion functions
Standing waves vs Moving waves
C6 Spectral resolution: 6th roots of unity and higher
Complete sets of coupling parameters and Fourier dispersion
Gauge shifts due to complex coupling
Introduction to CN beat dynamics and “Revivals” in Lecture 12
Web apps used:
(Geometry of U(2) characters - Ch. 6-9 of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 3-7 of Ch. 2)
C6 Spectral resolution: 6th roots of unity and higher
Complete sets of coupling parameters and Fourier dispersion
Gauge shifts due to complex coupling
Introduction to wave dynamics of phase, mean phase, and group velocity
Expo-Cosine identity
Relating space-time and per-space-time
Wave coordinates
Pulse-waves (PW) vs Continuous -waves (CW)
Wave coordinates for Linear Dispersion
Wave coordinates for Bohr-Schrodinger Dispersion
Einstein-L orentz-Minkowski laser coordinates
(Geometry of U(2) characters - Ch. 6-9 of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 3-7 of Ch. 2)
Wave coordinates in spacetime and per-spacetime for Bohr-Schrodinger Dispersion
Phase velocity for simple wave ei(kx-ωt): Newton’s “corpuscle” tracks vs. wave-zero paths
Slow L-wave eiL=ei(k(L)·x-ω(L)·t)
Fast R-wave eiR=ei(k(R)·x-ω(R)·t)
Phase velocity for wave pair eiL +eiR=S·D: Half-sum factor S=ei(L+R)/2
Group velocity for wave pair eiL +eiR=S·D: Half-difference factor D=ei(L-R)/2+e-i(L-R)/2
Introduction to wave coordinates by Left-moving and Right-moving laser beams
L-laser 600THz and R-laser 600THZ (Laser lab frame)
Phase P-vector and group G-vector span Cartesian spacetime coordinates
L′-laser 300THz and R′-laser 1200THZ (Doppler shifted in moving frame)
Doppler shifted L′-vector and R′-vector in (L, R)-per-spacetime
Vectors of phase P′=(R′+L′)/2 and group G′=(R′-L′)/2
Einstein-Lorentz-Minkowski “Relawavity” spacetime coordinates
Brief tour of and relativistic mechanics by geometry
Summary of optical wave parameters for relativity and QM
(Geometry of U(2) characters - Ch. 6-9 of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 3-7 of Ch. 2)
Two wave archetypes: Pulse-Wave (PW) versus Continuous-Wave (CW)
Comparing spacetime uncertainty (Δx or Δt) with per-spacetime bandwidth (Δκ or Δυ)
Introduction to beat dynamics and “Revivals” due to Bohr-dispersion
Relating ∞-Square-well waves to Bohr rotor waves
∞-Square-well wave dynamics
SinNx/x wavepacket bandwidth and uncertainty
∞-Square-well revivals: SinNx/x packet explodes! (and then UNexplodes!)
Bohr-rotor wave dynamics
Gaussian wave-packet bandwidth and uncertainty
Gaussian Bohr-rotor revivals and quantum fractals
Understanding fractals using geometry of fractions (Rationalizing rationals)
Farey-Sums and Ford-products
Discrete CN beat phase dynamics (Characters gone wild!)
The classical bouncing-ball Monster-Mash
Polygonal geometry of U(2) ⊃ CN character spectral function
Algebra
Geometry
(Geometry of U(2) characters - Ch. 6-12 of Unit 3)
(Principles of Symmetry, Dynamics, and Spectroscopy - Sec. 1-12 of Ch. 2)
Breaking N cyclic coupling into linear chains
Review of 1D-Bohr-ring related to infinite square well (and review of revival)
∞-Square well paths analyzed using Bohr rotor paths
Breaking C2N+2 to approximate linear N-chain
Band-It simulation: Intro to scattering approach to quantum symmetry
Breaking C2N cyclic coupling down to CN symmetry
Acoustical modes vs. Optical modes
Intro to other examples of band theory
Type-AB avoided crossing view of band-gaps
Finally! Symmetry groups that are not just CN
The “4-Group(s)” D2 and C2v
Spectral decomposition of D2
Some D2 modes
Outer product properties and the Crystal-Point Group Zoo
(QTCA Unit 5 Ch. 15; Int.J.Mol.Sci, 14, 714(2013) p.755-774)
(PSDS - Ch. 3)
|
3-Dihedral-axes group D3 vs. 3-Vertical-mirror-plane group C3v D3 and C3v are isomorphic (D3 ~ C3v share product table) Deriving D ~ C products: By group definition ⏐g〉=g⏐1〉 of position ket ⏐g〉 By nomograms based on U(2) Hamilton-turns Deriving D3 ~ C3v equivalence transformations and classes Non-commutative symmetry expansion and Global-Local solution Global vs Local symmetry and Mock-Mach principle Global vs Local matrix duality for D3 Global vs Local symmetry expansion of D3 Hamiltonian 1st-Stage spectral decomposition of global/local D Hamiltonian E operators) Group theory of equivalence transformations and classes Lagrange theorems All-commuting operators and D3-invariant class algebra (center) All-commuting projectors and D3-invariant characters Group invariant numbers: Centrum, Rank, and Order Spectral resolution to irreducible representations (or “irreps”) foretold by characters or traces Crystal-field splitting: O(3) ⊃ D3 symmetry reduction and Dℓ↓ D3 splitting |
|
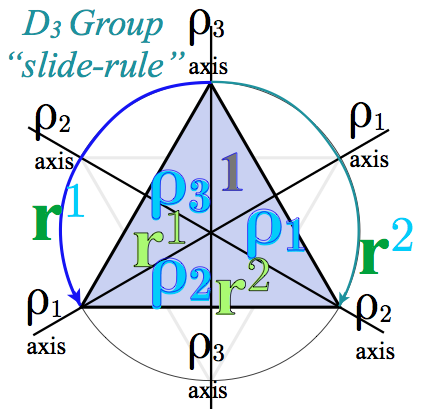
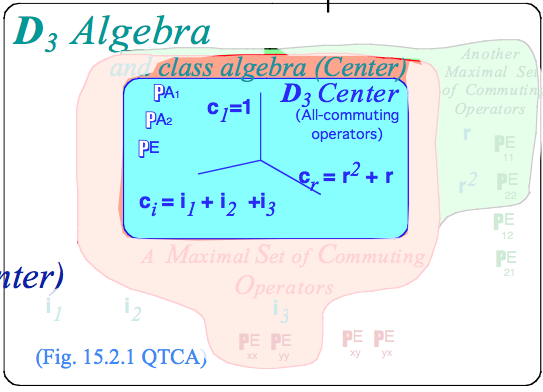
(Int.J.Mol.Sci, 14, 714(2013) p.755-774; QTCA Unit 5 Ch. 15)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 3)
|
Review: 1st-Stage Spectral resolution of D3 Center (Class algebra) Group theory of equivalence transformations and classes Lagrange theorems All-commuting class projectors D3-invariant character ortho-completeness Spectral resolution to irreducible representations (“irreps”) foretold by characters or traces Subgroup splitting or correlation frequency formula: f(α)(D(α)(G)↓H) Atomic ℓ-level or 2ℓ+1-multiplet splitting D3 examples for ℓ=1-6 Group invariant numbers: Centrum, Rank, and Order 2nd-Stage spectral decompositions of global/local D3 Splitting class projectors using subgroup chains D3 ⊃ C2 and D3 ⊃ C3 Splitting classes 3rd-stage spectral resolution to irreducible representations (irreps) and Hamiltonian eigensolutions Tunneling modes and spectra for D3 ⊃ C2 and D3 ⊃ C3 local subgroup chains |
|
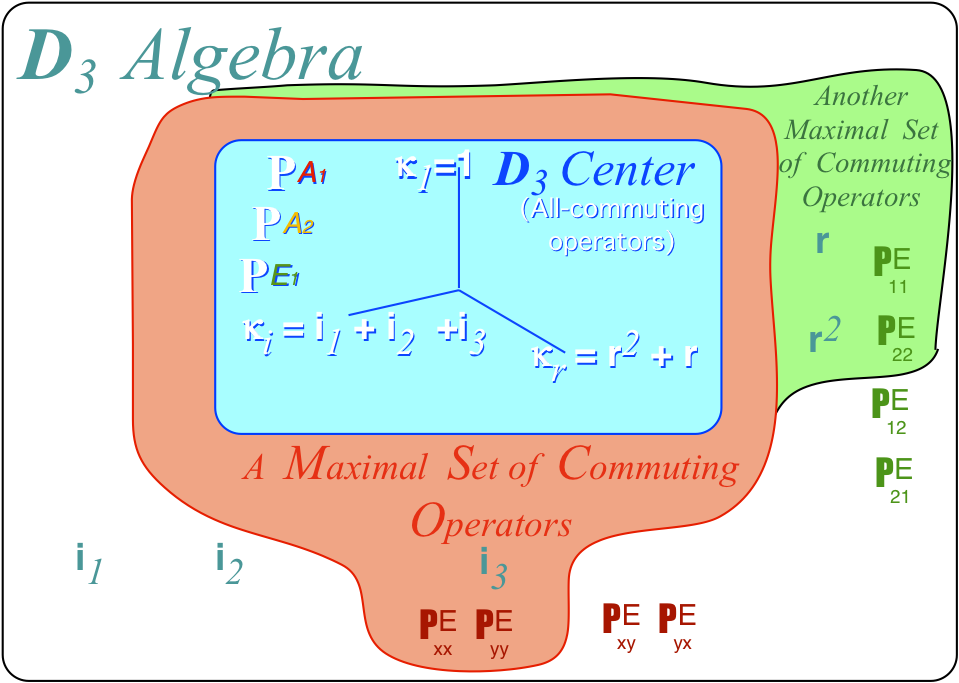
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 5 Ch. 15)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 4)
|
Review Stage 1: Group Center: Class-sums κg , characters χμ(g), and All-Commuting Projectors Pμ Review Stage 2: Group operators g and Mutually-Commuting projectors Pμkk Review Stage 3: Weyl g-expansion in irreps Dμjk(g) and Non-Commuting projectors Pμjk Simple matrix algebra Pμab Pνcd = δμνδbcPμad Pμjk transforms right-and-left Pμjk -expansion in g-operators Example of D3 transformation by matrix DEjk(r1) Details of Mock-Mach relativity-duality for D3 groups and representations Lab-fixed(Extrinsic-Global) vs. Body-fixed (Intrinsic-Local) Hamiltonian and D3 group matrices in global and local ⏐P(μ)〉-basis Hamiltonian and D3 group matrices in global and local ⏐P(μ)〉-basis Global vs. Local block rearrangement Hamiltonion eigen-matrix calculation Hamiltonian local-symmetry eigensolution Molecular vibrational mode eigensolution Local symmetry limit 1 Global symmetry limit (free or “genuine” modes) |
|
(Int.J.Mol.Sci, 14, 714(2013) p.755-774; QTCA Unit 5 Ch. 15)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 4)
Review: Hamiltonian local-symmetry eigensolution in global and local ⏐P(μ)〉-basis
Molecular vibrational modes vs. Hamiltonian eigenmodes
Molecular K-matrix construction
D3 ⊃ C2(i3) local-symmetry K-matrix eigensolutions
D3-direct-connection K-matrix eigensolutions
D3 ⊃ C3(r±1) local symmetry K-matrix eigensolutions
Applied symmetry reduction and splitting
Subduced irep Dα(D3)↓C2 = d02⊕d12⊕.. correlation
Subduced irep Dα(D3)↓C3 = d03⊕d13⊕.. correlation
Spontaneous symmetry breaking and clustering: Frobenius Reciprocity , band structure
Induced rep da(C2)↑D3 = Dα⊕Dβ⊕.. correlation
Induced rep da(C3)↑D3 = Dα⊕Dβ⊕.. correlation
D6 symmetry and Hexagonal Bands
Cross product of the C2 and D3 characters gives all D6 = D3 ×C2 characters and ireps
Induced rep da(C2)↑D6 = Dα⊕Dβ⊕.. correlation
Induced rep da(C6)↑D6 = Dα⊕Dβ⊕.. correlation
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 5 Ch. 15)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 4)
Review: Symmetry reduction and splitting: Subduced irep Dα(D3)↓C2 = d02⊕d12⊕.. correlation
Symmetry induction and clustering: Induced rep hda(C2)↑D3 =Dα⊕Dβ⊕.. correlation
Review: Review: Symmetry reduction and splitting: Subduced irep Dα(D3)↓C3 = d03⊕d23⊕.. correlation
Symmetry induction and clustering: Induced rep dc(C3)↑D3 =Dα⊕Dβ⊕.. correlation
D3-C2 Coset structure of dm2(C2)↑D3 induced representation basis
D3-Projection of dm2(C2)↑D3 induced representation basis
Derivation of Frobenius reciprocity
D6 ⊃ D2 ⊃ C2 = D3 ×C2 symmetry and outer product geometry
Irreducible characters
Irreducible representations
Correlations with D6 characters:
...and C2(i3) characters......and C6(1, h1, h2,...) characters
D6 symmetry and induced representation band structure
Introduction to octahedral and tetrahedral symmetry: Oh ⊃ O ~ Td ⊃ T
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 5 Ch. 15)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 4)
Introduction to octahedral/ tetrahedral symmetry Oh ⊃ O ~ Td ⊃ T
Octahedral-cubic O symmetry and group operations
Tetrahedral symmetry becomes Icosahedral
Octahedral groups Oh ⊃ O ~ Td ⊃ T
Octahedral O and spin-O ⊂ U(2)
Tetrahedral T class algebra
Tetrahedral T class minimal equations
Tetrahedral T class projectors and characters
Octahedral O class algebra
Octahedral O class minimal equations
Octahedral O class projectors and characters
Octahedral Oh ⊃ O: Inversion (g&u) parity
Octahedral Oh ⊃ O ⊃ CI subgroup correlations
Oh ⊃ O ⊃ D4 subgroup correlations
Oh ⊃ O ⊃ D4 ⊃ C4 subgroup correlations
Preview of applications to high resolution spectroscopy
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 5 Ch. 15)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 4)
Review: Octahedral Oh ⊃ O group operator structure
Review: Octahedral Oh ⊃ O ⊃ D4 ⊃ C4 subgroup chain correlations
Comparison of O ⊃ D4 ⊃ C4 and O ⊃ D4 ⊃ D2 correlations and level/projector splitting
O ⊃ D4 ⊃ C4 subgroup chain splitting
O ⊃ D4 ⊃ D2 subgroup chain splitting (nOrmal D2 vs. unOrmal D2)
Oh ⊃ O ⊃ D4 ⊃ C4 and Oh ⊃ O ⊃ D4 ⊃ C4v ⊃ C2v subgroup splitting
Splitting O class projectors Pμ into irreducible projectors Pμm4m4 for O ⊃ C4
Development of irreducible projectors Pμm4m4 and representations Dμm4m4
Calculating PE0404 , PE2424, PT10404, PT11414, PT22424, PT21414
O ⊃ C4 induced representation 04(C4)↑O ~ A1 ⊕ T1 ⊕ E and spectral analysis examples
Elementary induced representation 04(C4)↑O
Projection reduction of induced representation 04(C4)↑O
Introduction to ortho-complete eigenvalue-parameter relations
Examples in SF6 spectroscopy
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 5 Ch. 15)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 4)
Review: Calculating idempotent projectors Pμm,m of O ⊃ C4:
PE0404 , PE2424, PT10404, PT11414, PT22424, PT21414
Review: Coset factored splitting of O ⊃ D4 ⊃ C4 projectors
Review: Broken-class-ordered splitting of O ⊃ D4 ⊃ C4 projectors and levels
Subgroup-defined tunneling parameter modeling
Comparing two diagonal O ⊃ C4 parameter sets to SF6 spectra
Comparing two diagonal O ⊃ C3 parameter sets to SF6 spectra
Why O ⊃ C2 parameter sets require off-diagonal nilpotent Pμm,n (m≠n)
Irreducible nilpotent projectors Pμm,n (m≠n)
Using fundamental Pμm,n relations: ( from Lecture 16):
(a) Pμm,mgPμn,n=Dμm,n(g)Pμm,n
(b) g=ΣμΣm,nDμm,n(g)Pμm,n
(c) Pμm,n=(ℓμ/°G)ΣgDμ*m,n(g)g
Review of D3 ⊃ C2 ~ C3v ⊃ Cv
Calculating and Factoring PT11404 and PT11434
Structure and applications of various subgroup chain irreducible representations
Oh ⊃ D4h ⊃ C4v , Oh ⊃ D3h ⊃ C3v , Oh ⊃ C2v
Comparing Oh ⊃ D4h ⊃ D2h and Oh ⊃ D3d ⊃ C2 representations (T1 vector-type)
Examples of off-diagonal tunneling coefficients DE0424
Comparing Local C4, C3, and C2 symmetric spectra
When Local C2 symmetry dominates
Comparing off-diagonal O ⊃ C2 parameter sets to CH4 models with “cluster-crossings”
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 7 Ch. 20-22)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 8)
1-D a†a algebra of U(1) representations
Creation-Destruction a†a algebra
Eigenstate creationism (and destruction)
Vacuum state
1st excited state
Normal ordering for matrix calculation
Commutator derivative identities
Binomial expansion identities
Matrix 〈ana†n〉 calculations
Number operator and Hamiltonian operator
Expectation values of position, momentum, and uncertainty for eigenstate ⏐n〉
Harmonic oscillator beat dynamics of mixed states
Oscillator coherent states (“Shoved” and “kicked” states)
Translation operators vs. boost operators
Applying boost-translation combinations
Time evolution of coherent state
Properties of coherent state and “squeezed” states
2-D a†a algebra of U(2) representations and R(3) angular momentum operators
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 7 Ch. 21-22)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 8)
Review: 1-D a†a algebra of U(1) representations
Review: Translate T(a) and/or Boost B(b) to construct coherent state
Review: Time evolution of coherent state (and “squeezed” states)
2-D a†a algebra of U(2) representations and R(3) angular momentum operators
2D-Oscillator basic states and operations
Commutation relations
Bose-Einstein symmetry vs Pauli-Fermi-Dirac (anti)symmetry
Anti-commutation relations
Two-dimensional (or 2-particle) base states: ket-kets and bra-bras
Outer product arrays
Entangled 2-particle states
Two-particle (or 2-dimensional) matrix operators
U(2) Hamiltonian and irreducible representations
2D-Oscillator states and related 3D angular momentum multiplets
R(3) Angular momentum generators by U(2) analysis
Angular momentum raise-n-lower operators s+ and s-
SU(2) ⊂ U(2) oscillators vs. R(3) ⊂ O(3) rotors
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 7 Ch. 21-22)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 5, 7)
Review: 2-D a†a algebra of U(2) representations
Angular momentum generators by U(2) analysis
Angular momentum raise-n-lower operators s+ and s-
SU(2) ⊂ U(2) oscillators vs. R(3) ⊂ O(3) rotors
Angular momentum commutation relations
Key Lie theorems
Angular momentum magnitude and uncertainty
Angular momentum uncertainty angle
Generating R(3) rotation and U(2) representations
Applications of R(3) rotation and U(2) representations
Molecular and nuclear wavefunctions
Molecular and nuclear eigenlevels
Generalized Stern-Gerlach and transformation matrices
Angular momentum cones and high J properties
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 7 Ch. 21-25)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 5, 7)
Three (3) applications of R(3) rotation and U(2) unitary representations DJmn(α,β,γ)
1. Atomic and molecular DJ*mn(α,β,γ)-wavefunctions
“Mock-Mach” lab-vs-body-defined states |Jmn〉=PJmn|(0,0,0)〉=∫ d(α,β,γ)DJ*mn(α,β,γ)R(α,β,γ)|(0,0,0)〉
2. R(3) rotation and U(2) unitary DJmn(α,β,γ)-transformation matrices
General Stern-Gerlach and polarization transformations R(α,β,γ)|Jmn〉=Σm′ DJm'n(α,β,γ)|Jm'n〉
Angular momentum cones and high J properties
3. Atomic and molecular multipole Hamiltonian tensor operators Tqk and eigenvalues
Multipole Tqk expansion of asymmetric-rotor Hamiltonians H = AJx2+BJy2+CJz2
Multipole Tqk expansion of symmetric-rotor Hamiltonians H = BJx2+BJy2+CJz2
Rotational Energy Surfaces (RE or RES) of symmetric rotor and eigensolutions
Rotational Energy Surfaces (RE or RES) of asymmetric rotor and energy levels
Sketch of modern molecular electronic, vibrational, and rotational spectroscopy
Example of CO2 rovibrational (υ=0) ⇔ (υ=1) bands
Introduction to RE symmetry and RES analysis of rovibrational Hamiltonians
Asymmetric Top eigensolutions for J = 1, 2
Based on AMOP Lectures 14-20
(Int.J.Mol.Sci, 14, 714(2013) p.755-774 , QTCA Unit 7 Ch. 21-25)
(Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 5, 7)
Review: Symmetric rigid quantum rotor analysis of R(2) Hamiltonian H = BJx2+BJy2+CJz2
Review: Rotational Energy Surfaces (RE or RES) and R(3) ~ U(2) representations
Asymmetric rigid quantum rotor analysis of D2 Hamiltonian H = AJx2+BJy2+CJz2
RES and Multipole Tqk tensor expansions
Atomic or molecular R(3) ℓ-level or 2ℓ+1-multiplet splitting
R(3) ⊃ D2 character analysis of ℓ-level or 2ℓ+1-multiplet splitting in D2
Detailed angular momentum operator analysis for J = 1-2 for D2 symmetry
Asymmetric rotor levels and RES plots for high-J
Octahedral semi-rigid quantum rotor analysis of Oh Hamiltonian H = BJ•J + t044T[4]
Spherical rotor levels and RES plots of Oh tensor eigenvalues
R(3) ⊂ O(3) ⊃ Oh ⊃ O character analysis of ℓ-level or 2ℓ+1-multiplet splitting in O
SF6 spectral fine structure P(88)
CF4 spectral fine structure P(54)
Based on: QTCA Lectures 24-25 (2013); AMOP Lectures 17-18 (2014)
Int.J.Mol.Sci, 14, 714(2013) p.755-774; Computer Phys. Reports 8,319-394 (1988)
(QTCA Unit 7 Ch. 21-25; Principles of Symmetry, Dynamics, and Spectroscopy - Ch. 5, 7)
Review: Asymmetric rotor levels of H = AJx2+BJy2+CJz2 and RES plots
D2 ⊃ C2 symmetry correlation
Review: Spherical rotor levels and RES plots
Spectral fine structure of SF6, SiF4, C8H8, ...
O ⊃ C4 and O ⊃ C3 symmetry correlation
Some more examples of J=30 levels (including T[6] vs T[4] effects)
Details of P(88) v4 SF6 and P(54) v4 CF4 spectral structure and implications
Beginning theory
Rovibronic nomograms and PQR structure
Rovibronic energy surfaces (RES) and cone geometry
Spin symmetry correlation, tunneling, and entanglement
Hyperfine vs. superfine structure (Case 1. vs Case 2.)
Spin-0 nuclei give Bose Exclusion
The spin-symmetry species mixing problem
Analogy between PE surface dynamics and RES
Rotational Energy Eigenvalue Surfaces (REES)