 & 1/21/2016
& 1/21/2016  )
)
| Animating Header Color | |
| Main Text Color | |
| Font Style |
 & 1/21/2016
& 1/21/2016  )
)
(Ch. 1 and Ch. 2 of Unit 1)
Geometry of momentum conservation axiom (ala Occam’s Razor)
Totally Inelastic “ka-runch”collisions* (begin 4:1 graph project)
Perfectly Elastic “ka-bong” and Center Of Momentum (COM) symmetry*
+Intro to weighty-averages and vector notation
Comments on idealization in classical models
Geometry of Galilean translation symmetry
45° shift in (V1,V2)-space
Time reversal symmetry
... of COM collisions
Algebra, Geometry, and Physics of momentum conservation axiom
Vector algebra of collisions
Matrix or tensor algebra of collisions
Deriving Energy Conservation Theorem
Numerical details of collision tensor algebra
2016 Honors Physics Colloquium web site
Link → http://www.uark.edu/ua/modphys/markup/HPColloqWeb.html
* Launch Vehicle Collision Simulator
Link → http://www.uark.edu/ua/modphys/markup/CMMotionWeb.html
* Launch Superball Collision Simulator
Link → http://www.uark.edu/ua/modphys/markup/BounceItWeb.html
Graph Paper: R for display on right side (i.e. Even numbered pages)
SUVVW To Fit 8x10
SUVVW To Fit 8x10R
SUV VW 240x80
SUVVW 240x80R
 & 1/28/2016
& 1/28/2016  )
)
(Ch. 2 to Ch. 4 of Unit 1)
Review of elastic Kinetic Energy ellipse geometry
The X2 Superball pen launcher*
Perfectly elastic “ka-bong” velocity amplification effects (Faux-Flubber)
Geometry of X2 launcher bouncing in box
Independent Bounce Model (IBM)
Geometric optimization and range-of-motion calculation(s)
Integration of (V1,V2) data to space-time plots (y1(t),t) and (y2(t),t) plots
Integration of (V1,V2) data to space-space plots (y1, y2)
Examples: (M1=7, M2=1) and (M1=49, M2=1)
Multiple collisions calculated by matrix operator products
Matrix or tensor algebra of 1-D 2-body collisions
Ellipse rescaling-geometry and reflection-symmetry analysis
Rescaling KE ellipse to circle
How this relates to Lagrangian, l’Etrangian, and Hamiltonian mechanics in Ch. 12
Graph Paper: Fine Protractor
 )
)
(Ch. 2 to Ch. 4 of Unit 1)
Review of elastic Kinetic Energy ellipse geometry
The X2 Superball pen launcher*
Perfectly elastic “ka-bong” velocity amplification effects (Faux-Flubber)
Geometry of X2 launcher bouncing in box
Independent Bounce Model (IBM)
Geometric optimization and range-of-motion calculation(s)
Integration of (V1,V2) data to space-time plots (y1(t),t) and (y2(t),t) plots
Integration of (V1,V2) data to space-space plots (y1, y2)
Examples: (M1=7, M2=1) and (M1=49, M2=1)
Multiple collisions calculated by matrix operator products
Matrix or tensor algebra of 1-D 2-body collisions
Ellipse rescaling-geometry and reflection-symmetry analysis
Rescaling KE ellipse to circle
How this relates to Lagrangian, l’Etrangian, and Hamiltonian mechanics in Ch. 12
Reflections in the clothing store: “It’s all done with mirrors!”
Introducing hexagonal symmetry D6~C6v (Resulting for m1/m2=3)
Group multiplication and product table
Classical collision paths with D6~C6v (Resulting from m1/m2=3)
Other not-so-symmetric examples: m1/m2=4 and m1/m2=7 and (M1=100, M2=1)
 ) & (2/9/2016
) & (2/9/2016  )
)
(Ch. 5 of Unit 1)
Review of (V1,V2)→(y1,y2) relations High mass ratio M1/m2 = 49
Force “field” or “pressure” due to many small bounces
Force defined as momentum transfer rate
The 1D-Isothermal force field F(y)=const./y and the 1D-Adiabatic force field F(y)=const./y3
Potential field due to many small bounces
Example of 1D-Adiabatic potential U(y)=const./y2
Physicist’s Definition F=-ΔU/Δy vs. Mathematician’s Definition F=+ΔU/Δy
Example of 1D-Isothermal potential U(y)=const. ln(y)
“Monster Mash”classical segue to Heisenberg action relations
Example of very very large M1 ball-wall(s) crushing a poor little m2
How does m2 conserve action (ΔxΔp or ∫p⋅dx) as its KE changes?
 &
(2/10/2016
&
(2/10/2016  )
)
(Comparing wave dynamics to classical behavior in Ch. 3 thru Ch. 5 of Unit 1)
Introducing lightwave Fourier analysis - Pulse Waves (PW) versus Continuous Waves (CW)
Simplest is CW (Continuous Wave, Cosine Wave, Colored Wave, Complex Wave,...)
CW parameters: Wavelength λ and Wave period τ
CW inverse parameters: Wavelnumber κ=1/λ and Wave frequency υ =1/τ
CW angular parameters: Wavevector k =2πκ=2π/λ and angular frequency ω =2πυ =2π/τ
CW wavefunction : ψ=A exp[i(kx-ωt)]= A cos(kx-ωt)+iA sin(kx-ωt)
Wave phasors, phasor chain plots, dispersion functions ω(k), and phase velocity Vphase=ω(k)/k
Special case: Lightwave linear dispersion:Vphase=c or: ω(k)=ck
Introducing PW (Pulse Wave, Particle-like Wave, Packet Wave,...) archetypes compared to CW
Building PW from CW components using “Fourier Control” app-panel
Fourier PW “box-car” geometric series summed
Animation of PW obeying lightwave linear dispersion ω(k)=ck
Important Evenson axiom for relativity: “All go c”
Visualizing PW wave uncertainty relations for space: Δx⋅Δκ=1 and time: Δt⋅Δυ=1
PW “wrinkles” go away if Fourier “boxcar” is tapered to a softer “Gaussian”
Opposite-pair CW (colliding ±m=±2) Fourier components trace a Cartesian space-time grid

(Quantum wave analogies to classical “Monster-Mash” model in Ch. 5 of Unit 1)
Reviewing lightwave Fourier analysis - Pulse Waves (PW) versus Continuous Waves (CW)
Opposite-pair CW (colliding ±m=±2) Fourier components trace a Cartesian space-time grid
Colliding PW lightwaves trace space-time “baseball diamonds”
Introducing CW (colliding ±m=±2) Doppler shifted to (m=-1 and m=+4)
NON-Lightwaves whose ω(k) dispersion functions are NOT straight lines
Animating PW made of CW that have quadratic (Bohr-Schrodinger) dispersion
Visualizing PW wave uncertainty relations for space: Δx⋅Δκ=1 and time: Δt⋅Δυ=1
Matter-wave fractal behavior in a “Tiny-Big-Bang”
[Harter, J. Mol. Spec. 210, 166-182 (2001)];
[Harter, Li IMSS (2012)]
A lesson in geometry of fractions and fractals: Ford Circles and Farey Sums
[Lester. R. Ford, Am. Math. Monthly 45,586(1938)];
[John Farey, Phil. Mag.(1816) Wolfram];
[Li, Harter, Chem.Phys.Letters (2015]

(Ch. 6 and part of Ch. 7 of Unit 1)
Potential energy geometry of Superballs and related things
Thales geometry and “Sagittal approximation”
Geometry and dynamics of single ball bounce
(a) Constant force F=-k (linear potential V=kx )
Some physics of dare-devil diving 80 ft. into kidee pool
(b) Linear force F=-kx (quadratic potential V=½kx2 (like balloon))
(c) Non-linear force (like superball-floor or ball-bearing-anvil)
Geometry and potential dynamics of 2-ball bounce
A parable of RumpCo. vs CrapCorp. (introducing 3-mass potential-driven dynamics)
A story of USC pre-meds visiting Whammo Manufacturing Co.
Geometry and dynamics of n-ball bounces
Analogy with shockwave and acoustical horn amplifier
Advantages of a geometric m1, m2, m3,... series
A story of Stirling Colgate (Palmolive) and core-collapse supernovae
Many-body 1D collisions
Elastic examples: Western buckboard
Bouncing columns and Newton’s cradle
Inelastic examples: “Zig-zag geometry” of freeway crashes
Super-elastic examples: This really is “Rocket-Science”

(Ch. 8 of Unit 1)
Geometry of common power-law potentials
Geometric (Power) series
“Zig-Zag” exponential geometry
Projective or perspective geometry
Parabolic geometry of harmonic oscillator kr2/2 potential and -kr1 force fields
Coulomb geometry of -1/r-potential and -1/r2-force fields
Compare mks units of Coulomb Electrostatic vs. Gravity
Geometry of idealized “Sophomore-physics Earth”
Coulomb field outside Isotropic & Harmonic Oscillator (IHO) field inside
Contact-geometry of potential curve(s)
“Crushed-Earth” models: 3 key energy “steps” and 4 key energy “levels”
Earth matter vs nuclear matter:
Introducing the “neutron starlet” and “Black-Hole-Earth”
Introducing 2D IHO orbits and phasor geometry
Phasor “clock” geometry
Graph Paper:
Cartesian

(Ch. 8 and Ch. 9 of Unit 1)
“Sophomore-Physics-Earth” models: 3 key energy “steps” and 4 key energy “levels”
“Crushed-Earth” models: 3 key energy “steps” and 4 key energy “levels”
Earth matter vs nuclear matter:
Introducing the “neutron starlet”
Fantasizing a “Black-Hole-Earth”
Introducing Isotropic Harmonic Oscillator (IHO) energy and frequency relations
Constructing 2D-IHO orbits using Kepler anomaly plots
Mean-anomaly and eccentric-anomaly geometry with web-app animation
Calculus and vector geometry of IHO orbits
Constructing 2D-IHO orbits using orbital phasor-clock plots
Phasor geometry of coordinate (x,y) and velocity (Vx,Vy) space with web-app animation
Kepler“laws” (Some that apply to all central (isotropic) F(r) force fields)
Angular momentum invariance of IHO: F(r)=-k·r with U(r)=k·r2/2
Angular momentum invariance of Coulomb: F(r)=-GMm/r2 with U(r)=-GMm·/r
Total energy E=KE+PE invariance of IHO: F(r)=-k·r
Total energy E=KE+PE invariance of Coulomb: F(r)=-GMm/r2
Link → BoxIt - Simulation of IHO Orbits w/ time rates of change
Link → RelaWavity - Geometry of IHO orbits w/ time rates of change
Link → RelaWavity - Geometry of IHO Ellipse Exegesis
 &
(3/3/2016
&
(3/3/2016  )
)
(Ch. 10 of Unit 1)
|
1. The Story of e (A Tale of Great $Interest$) How good are those power series? Taylor-Maclaurin series, imaginary interest, and complex exponentials 2. What good are complex exponentials? Easy trig Easy 2D vector analysis Easy oscillator phase analysis Easy rotation and “dot” or “cross” products 3. Easy 2D vector calculus Easy 2D vector derivatives Easy 2D source-free field theory Easy 2D vector field-potential theory 4. Riemann-Cauchy relations (What’s analytic? What’s not?) Easy 2D curvilinear coordinate discovery Easy 2D circulation and flux integrals Easy 2D monopole, dipole, and 2n-pole analysis Easy 2n-multipole field and potential expansion Easy stereo-projection visualization Cauchy integrals, Laurent-Maclaurin series 5. Mapping and Non-analytic 2D source field analysis |
1. Complex numbers provide "automatic trigonometry" 2. Complex numbers add like vectors. 3. Complex exponentials Ae-iωt track position and velocity using Phasor Clock. 4. Complex products provide 2D rotation operations. 5. Complex products provide 2D “dot”(•) and “cross”(x) products. 6. Complex derivative contains “divergence”(∇•F) and “curl”(∇xF) of 2D vector field 7. Invent source-free 2D vector fields [∇•F=0 and ∇xF=0] 8. Complex potential φ contains “scalar”( F= ∇Φ) and “vector”( F=∇xA) potentials. The half-nʼ-half results: (Riemann-Cauchy Derivative Relations) 9. Complex potentials define 2D Orthogonal Curvilinear Coordinates (OCC) of field 10. Complex integrals ∫ f(z)dz count 2D “circulation”( ∫F•dr) and “flux”( ∫Fxdr) 11. Complex integrals define 2D monopole fields and potentials 12. Complex derivatives give 2D dipole fields 13. More derivatives give 2D 2N-pole fields… 14. ...and 2N-pole multipole expansions of fields and potentials... 15. ...and Laurent Series... 16. ...and non-analytic source analysis. |

(Ch. 2 of Unit 2)
1D forced-damped-harmonic oscillator equations and Green’s function solutions
Linear harmonic oscillator equation of motion.
Linear damped-harmonic oscillator equation of motion.
Frequency retardation and amplitude damping.
Figure of oscillator merit (the 5% solution 3/Γ and other numbers)
Linear forced-damped-harmonic oscillator equation of motion.
Phase lag and amplitude resonance amplification
Figure of resonance merit: Quality factor q=ω0/2Γ
Properties of Green’s function solutions and their mathematical/physical behavior
Transient solutions vs. Steady State solutions
Complete Green’s Solution for the FDHO (Forced-Damped-Harmonic Oscillator)
Quality factors: Beat, lifetimes, and uncertainty
Approximate Lorentz-Green’s Function for high quality FDHO (Quantum propagator)
Common Lorentzian (a.k.a. Witch of Agnesi)

(Ch. 3-4 of Unit 2)
|
Review of 1D FDHO (Forced-Damped-Harmonic Oscillator) response 2D harmonic oscillator (2D-HO) equations of motion Lagrangian and matrix forms 2D harmonic oscillator equation eigensolutions (normal modes) Eigensolutions by geometry for 2D-HO with bilateral (B-Type) symmetry Symmetric (low frequency) mode versus antisymmetric (high frequency) mode Mixed mode beat dynamics (with constant π/2 phase-lag) Eigensolutions by matrix-algebra with example M = Secular equation Hamilton-Cayley equation and projectors Idempotent projectors (how eigenvalues ⇒ eigenvectors) Operator orthonormality and Completeness (Idempotent means: P·P=P) Spectral Decompositions Functional spectral decomposition Orthonormality vs. Completeness vis-a`-vis Operator vs. State Lagrange functional interpolation formula Diagonalizing Transformations (D-Ttran) from projectors |

(Ch. 3-4 of Unit 2)
|
Review of 1D FDHO (Forced-Damped-Harmonic Oscillator) response 2D harmonic oscillator (2D-HO) equations of motion Lagrangian and matrix forms 2D harmonic oscillator equation eigensolutions (normal modes) 2D classical HO compared to U(2) quantum 2-state system Introducing ABCD Hamilton Pauli spinor symmetry expansion Eigensolutions by geometry for 2D-HO with bilateral (B-Type) symmetry Symmetric (low frequency) mode versus antisymmetric (high frequency) mode Mixed mode beat dynamics (with constant π/2 phase-lag) Geometry of phase and polarization Eigensolutions by matrix-algebra with example M = Secular equation Hamilton-Cayley equation and projectors Idempotent projectors (how eigenvalues ⇒ eigenvectors) Operator orthonormality and Completeness (Idempotent means: P·P=P) Spectral Decompositions Functional spectral decomposition Orthonormality vs. Completeness vis-a`-vis Operator vs. State Lagrange functional interpolation formula Diagonalizing Transformations (D-Ttran) from projectors |

Video of Coupled Pendula |
(Ch. 3-4 of Unit 2)

(Ch. 3-4 of Unit 2)
|
Review of 2D classical HO compared to U(2) quantum 2-state system Introducing ABCD Hamilton Pauli spinor symmetry expansion Algebra of Hamilton/Pauli hypercomplex operators {σA,σB,σC}={σZ,σX,σY} σA-products 3D vector analysis and “Crazy-Thing-Theorem” Eigensolutions by matrix-algebra with example M = Secular equation Hamilton-Cayley equation and projectors Idempotent (P·P=P) projectors (how eigenvalues ⇒ eigenvectors) Eigenvector orthonormality and completeness Spectral Decompositions unctional spectral decomposition U(2)⊃C2 ABCD group theory method to find 2D-HO eigenmodes and eigenvalues Asymmetric-diagonal (AD-Type) symmetry Bilateral-balanced (B-Type) symmetry Circular-chiral-cycloton (C-Type) symmetry Mixed ABCD symmetry examples More theory of matrix diagonalization Lagrange functional interpolation formula Diagonalizing Transformations (D-Ttran) from projectors |

|
(Ch. 4 of Unit 2)
|
Review: 2D harmonic oscillator equations with Lagrangian and matrix forms ANALOGY: 2-State Schrodinger: iħ∂t|Ψ(t)〉=H|Ψ(t)〉 versus Classical 2D-HO: ∂2tx=-K•x Hamilton-Pauli spinor symmetry ( σ-expansion in ABCD-Types) H=ωμσμ Derive σ-exponential time evolution (or revolution) operator U = e-iHt = e-iσµωµt Spinor arithmetic like complex arithmetic Spinor vector algebra like complex vector algebra Spinor exponentials like complex exponentials ("Crazy-Thing"-Theorem) Geometry of evolution (or revolution) operator U = e-iHt = e-iσµωµt The "mysterious" factors of 2 (or 1/2): 2D Spinor vs 3D Spin Vector space 2D Spinor vs 3D vector rotation NMR Hamiltonian: 3D Spin Moment m in B field Euler's state definition using rotations R(α,0,0), R(0,β,0),and R(0,0,γ) Spin-1 (3D-real vector) case Spin-1/2 (2D-complex spinor) case 3D-real Stokes Vector defines 2D-HO polarization ellipses and spinor states Asymmetry SA=SZ, Balance SB =SX, and Chirality SC =SY Polarization ellipse and spinor state dynamics The "Great Spectral Avoided-Crossing" and A-to-B-to-A symmetry breaking |
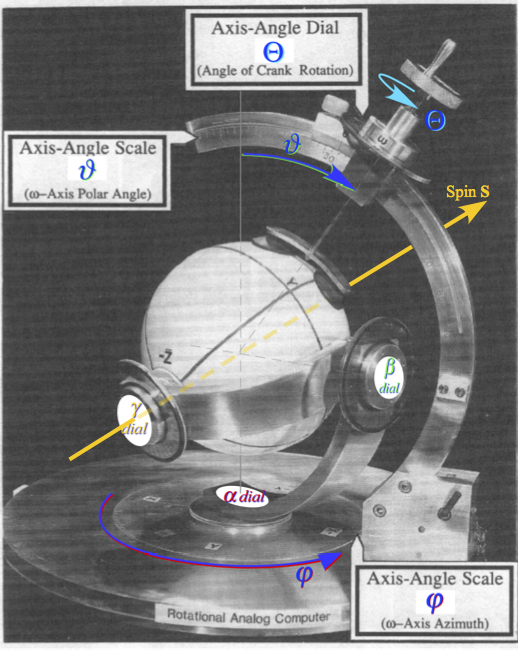
|
(Ch. 7-8 of Unit 4 11.24.15)

(Ch. 5 of Unit 4 3.29.15)
Wave resonance in cyclic CN symmetry
Harmonic oscillator with cyclic C2 symmetry
C2 symmetric (B-type) modes
Projector analysis of 2D-HO modes and mixed mode dynamics
½-Sum-½-Diff-Identity for resonant beat analysis
½-Sum-½-Diff-Identity for resonant beat analysis
Mode frequency ratios and continued fractions
Geometry of that 90°-phase lag (again)
Harmonic oscillator with cyclic C3 symmetry
C3 symmetric spectral decomposition by 3rd roots of unity
Deriving C3 projectors
Deriving and labeling moving wave modes
Deriving dispersion functions and degenerate standing waves
Examples by WaveIt animation
C6 symmetric mode model: Distant neighbor coupling
C6 moving waves and degenerate standing waves
C6 dispersion functions for 1st, 2nd, and 3rd-neighbor coupling
C6 dispersion functions split by C-type symmetry(complex, chiral, ...)
C12 and higher symmetry mode models: Archetypes of dispersion functions and 1-CW phase velocity
½-Sum-½-Diff-theory of 2-CW group and phase velocity
(Ch. 5 of Unit 4 3.29.15)

(Ch. 5 of Unit 4)
Wave resonance in cyclic CN symmetry
C6 symmetric mode model: Distant neighbor coupling
C6 moving waves and degenerate standing waves
C6 dispersion functions for 1st, 2nd, and 3rd-neighbor coupling
C6 dispersion functions split by C-type symmetry(complex, chiral, ...)
C12 and higher symmetry mode models: Archetypes of dispersion functions and 1-CW phase velocity
½-Sum-½-Diff-theory of 2-CW group and phase velocity
Given two 1-CW phases find 2-CW phase velocity Vphase(2-CW) and group velocity Vgroup (2-CW)
Example: Bohr Dispersion 2-CW made of 1-CW(m=-1) and 1-CW(m=2)
2-CW space-time (x,t) lattice from per-space-time (κ,υ) by algebra
Same Example

(Unit 3 4.05.16)
Special Relativity and Quantum Mechanics regarded as mysterious and lacking clarity
Bob & Alice regard for clarity of SR: foggy or QM: opaque
Can this situation be improved at fundamental axiomatic level?
Evidence and concepts needing critical review:
QM (Planck, 1900) and SR (Einstein, 1905) are both about light (em waves)
Galilean relativity, how it fails for light and how it doesn’t
The great light-wave speed-limit (c=2.99792458m/s. by Evenson,...,Hall 1972)
Need better axioms (Occam’s Razors & Evenson’s Lasers): CW axioms outwit old PW axioms
Introduce “Keyboard of the gods” CW per-space-time (к,υ) that rules (λ,τ) space-time
Introduce idea of quantized wavenumber-кn and amplitude An (1st and 2nd quantization)
Introduce infrared (IR) 300 THz, green 600THz, and ultra-violet (UV) 1200THz CW laser beams
Optical Doppler CW frequency shift υA/υB: A hidden key to understanding modern physics
Bob and Alice deduce Evenson’s CW Axiom: All march together at c = υλ = υ/к
Bob, Alice, and Carla discover rapidity (ρAB=ln υA/υB), a longitudinal measure of speed
Bob, Alice, and Carla get Galileo’s Revenge Part I.: ρCB=ρCA+ρAB , a simple speed sum
Bob, Alice, and Carla get Galileo’s Revenge Part II.:and map space-time by phase-group 2-CW
½-sum-½-difference of phasor angular velocity determines space-time geometry
Relating rapidity ρAB and relativity velocity parameter βAB=uAB/c

(Unit 3 4.05.16)
Review of Doppler-shift and Rapidity ρAB calculation: Galileo’s Revenge Part I Lect. 23 p.64-75
Relating rapidity ρAB and relativity velocity parameter βAB=uAB/c
Review of ½-sum-½-difference Phase and Group factors giving relativistic space-axes and time-axes
Colliding-CW space-time (x,ct)-graph vs Colliding PW space-time (R,L)-baseball diamond
Review of ½-sum-½-difference of phasor angular velocity:Galileo’s Revenge Part II (Pirelli site)
Elementary models: 2-comb Moire′ patterns and cosine-law constructions
Bob, Alice, and Carla combine Doppler shifted ½-sum-½-difference Phase and Group factors
Doppler shifted Phase vector P′ and Group vector G′ in per-space-time
Minkowski coordinate grid in space-time
Animations that compare Doppler shifted colliding CW with colliding PW
The 16 parameters of Doppler-shifted 2-CW Minkowski geometry
Doppler shifted Phase parameters
Doppler shifted Group parameters
Lorentz transformation matrix and Two Famous-Name Coefficients
Thales Mean Geometry (Thales of Miletus 624-543 BCE) and its role in Relawavity
Detailed geometric construction of relawavity plot for 1-octave Doppler (βAB=uAB/c=3/5)
Stellar aberration and the Epstein approach to SR

(Unit 3 4.12.16)
Review: Rapidity ρ=ρAB, Doppler shifts e±ρ, and SR velocity parameter Vgroup/c=βAB=uAB/c=tanhρAB
Geometric construction steps 1-4 : 1-octave Doppler (e+ρ=2, e-ρ=1/2), (βAB=uAB/c=3/5)
Reviewing wave coefficients we’ll need to know (backwards and forwards)
Comparison of group and phase dynamics: FAST(er) (β=u/c=3/5) vs SLOW(er) (β=u/c=1/5)
Thales Mean Geometry (Thales of Miletus 624-543 BCE) and its role in Relawavity
Geometric construction steps 5,6,...: Per-space-time (ω,ck) dispersion hyperbola ω = Bcoshρ...
A quick flip to space-time (ct,x) construction: Minkowski coordinate grid
Lorentz transformations of Phase vector P′ and Group vector G′ in per-space-time
Lorentz matrix transformation of (x,ct) space-time coordinates
Two Famous-Name Coefficients: Lorentz space contraction and Einsein time dilation
Heighway Paradoxes: A relativistic “He said-She-said” argument
Phase invariance...derives Lorentz transformations
Another view: phasor-invariance and proper time
Yet another view: The Epstein space-proper-time approach to SR

(Unit 3 4.14.16)
Review of geometric construction , per-space-time (ω,ck) dispersion hyperbola ω = Bcoshρ...
A quick flip to space-time (ct,x) construction: Minkowski coordinate grid
Lorentz transformations of Phase vector P′ and Group vector G′ in per-space-time
Lorentz matrix transformation of (x,ct) space-time coordinates
Two Famous-Name Coefficients: Lorentz space contraction and Einsein time dilation
Heighway Paradoxes: A relativistic “He said-She-said” argument
Phase invariance...derives Lorentz transformations...and vice-versa
Another view of phasor-invariance
Geometry of invariant hyperbolas
Algebra of invariant hyperbolas
Proper time τ0 and proper frequency ω0
A politically incorrect analogy of rotation to Lorentz transformation
Yet another view: The Epstein space-proper-time approach to SR uses stellar aberration angle σ
Relating rapidity ρ to stellar aberration angle σ and circular or hyperbolic arc-area
Each circular trig function has a hyperbolic “country-cousin” function
Ship vs Lighthouse sagas and the Bureau of Inter-Galactic Aids to Navigation at Night (Our 1st RelativIt animations).

(Unit 3 p.19-32 - 4.19.16)
Ship vs Lighthouse sagas and the Bureau of Inter-Galactic Aids to Navigation at Night (Our 1st RelativIt animations).
2005 and 2016 animations of lighthouses and ships in (x,y) scenarios and Minkowski (x,ct) plots
Lighthouse (x,y) frame: Dual concentric circular wavefronts serve as timing device
Ship frame: time dilation Δ=coshρ=1.15 of Lighthouse blinks
Simultaneous events in Lighthouse (x,y) frame: Not so in Ship (x′,y′) frame
Simultaneous events in Lighthouse (x,y) frame: Not so in Ship (x′,y′) frame
Overlapped Lighthouse (x,ct) and Ship (x′,ct′) frame Minkowski plots correlate inconsistencies
Ship (x′,y′) frame: Dual un-concentric circular wavefronts map space-time
Pythagorean derivation of time-dilation factor Δ=coshρ
Un-concentric derivation of stellar aberration k-angle σ
Per-spacetime 4-vector (ω0,ωx,ωy,ωz) =(ω,ckx,cky,ckz) transformation
“Occam-sword” geometry: A pattern recognition aid
Relating velocity parameter β=u/c to rapidity ρ to k-angle σ to u/c-angle ν
Circular arc-area σ vs. hyperbolic arc-area ρ
Each circular trig function has a hyperbolic “country-cousin” function
Yet another view: The Epstein space-proper-time approach to SR uses stellar aberration k-angle σ

(Unit 3 p.28-42 - 4.21.16)
A neo-liberal trigonometry lesson (sine, tangent, and secant) functions of angular sector area σ
Complimentary functions (... cosine, and cotangent, cosecant)
Hyper-trigonometry of ( tanhρ, sinhρ, and coshρ, sechρ, and cschρ, cothρ )
Functions of hyper-angular sector area ρ related to functions of σ
Each circular trig function has a hyperbolic “country-cousin” function
...and big-party fun was had by all!
Pattern recognition aids and “Occam-sword” geometry
Relating velocity parameters β=u/c to rapidity ρ to k-angle σ to u/c-angle ν
Relating wave dimensional parameters of phase wave and group wave
Parameter-space symmetry points
Yet another view: The Epstein space-proper-time approach to SR uses stellar aberration k-angle σ
Review of proper time relations and basis of Epstein’s cosmic speedometer
Epstein geometry for relativistic parameters
Spectral details of per-spacetime 4-vector (ω0,ωx,ωy,ωz) =(ω,ckx,cky,ckz) transformation

(Unit 3 p.28-42)
Review of hyper-trigonometry ( tanhρ, sinhρ, and coshρ, sechρ, and cschρ, cothρ )
and co-trigonometry ( sinσ, tanσ, and secσ, cosσ, and cotσ, cscσ )
Review of “Occam-sword” geometry and wave parameters for phase and group motion
Wave parameter symmetry points
Yet another view: Epstein’s space-proper-time approach to SR and stellar aberration k-angle σ
Review of proper time relations and basis of Epstein’s cosmic speedometer
Epstein vs Einstein-Minkowski geometry of relativity
Einstein time dilation
Lorentz space contraction
Time-simultaneity-breaking
Velocity addition
Twin-paradox resolution in space-proper-time
Spectral details of per-spacetime 4-vector (ω0, ωx, ωy, ωz) =(ω, ckx, cky, ckz) transformation

(Unit 3 p.45-61)
Using (some) wave parameters to develop relativistic quantum theory
Low rapidity approximations to υphase and cκphase match to Newtonian KE and momentum
How Mc2 pops right up
Exact υphase gives exact Planck-Einstein energy formulas (1900-1905)
Exact cκphase gives exact Bohr momentum and dispersion formulas (1921-1927)
Bohr-Schrodinger approximation to dispersion (Who threw away the Mc2 ?!!)
“What’s the Matter with Mass?” Definition(s) of relativistic and quantum mechanical mass
(1) Einsteinian rest mass (2) Galilean momentum mass (3) Newtonian effective mass
Three Faces of Eve: A photon’s split-mass personality
Relativistic action S and Lagrangian-Hamiltonian relations: How invariant phase works
The Legendre transformation relations
Deriving Lagrangian and Hamiltonian functions
Geometry of 1st Lagrangian and 1st Hamiltonian equations
Poincare invariant action differential
Hamilton-Jacobi equations
How Hamilton-Jacobi derives Schrodinger-op equations
How Huygens contact transformations determine motion

(Unit 3 p.45-64)
Review of wave parameters used to develop relativistic quantum theory
Bohr-Schrodinger (BS) approximation throws out Mc2 (Is frequency really relative?)
Effect on group velocity (None) and phase velocity (Absurd)
1st Quantization: Quantizing phase variables km and ω(km)
Understanding how quantum dynamics and transitions involve “mixed” states
Square well example of mixing unequal frequencies
Circle well or ring example of mixing equal or unequal frequencies
Mixing unequal amplitudes makes “Galloping” wave: Analogy of (SWR, SWQ) to (Vgroup, Vphase)
Analogy with optical polarization geometry and Kepler orbits
Super-luminal speed and Feynman-Wheeler pair-creation switchbacks
2nd Quantization: Quantizing wave amplitudes AN and invariance of photon number
Analogy 1: Many CW (Continuous Waves) add up to make PW (Pulse Waves)
Analogy 2: Many Photon-Number-Modes add up to make Coherent-Laser-Modes
Heisenberg ΔυΔt~1~ΔκΔx analogous to ΔNΔphase~1 uncertainty relations
Electromagnetic wave mode energy: Maxwell vs. Planck-Einstein
1st quantization for wave phase variables and classical energy of E, B , and A fields
2nd quantization for wave and Planck quantum energy of E, B , and A fields
Scaling E-waves to mime quantum Ψ-waves and ψ-waves
Relativistic effects on charge, current, and Maxwell Fields

(Unit 3 p.45-61 - 4.26.16)
Relativity relates charge, current, and magnetic fields
Geometric derivation of magnetic constant μ0 from electric ε0
Lorentz-Poincare symmetry and energy-momentum spectral conservation rules
Review of 2nd-quantization “photon” number N and 1st-quantization wavenumber κ=m
Sketches of atomic and molecular spectroscopy
Relativistic optical transitions and Compton recoil formulae
Feynman diagram geometry
Recoils shifts
Compton recoil related to rocket velocity formula
Geometric transition coordinate grids
Relawavity in accelerated frames
Relawavity in accelerated frames
Analysis of constant-g grid compared to zero-g Minkowski frame
Animation of mechanics and metrology of constant-g grid