

2014 Detailed List of Lecture Topics
 Part 2
Part 2  Part 3
Part 3 
(Ch. 1 and Ch. 2 of Unit 1)
Geometry of momentum conservation axiom
Totally Inelastic “ka-runch”collisions*
Perfectly Elastic “ka-bong” and Center Of Momentum (COM) symmetry*
Comments on idealization in classical models
Geometry of Galilean translation symmetry
45° shift in (V1,V2)-space
Time reversal symmetry
... of COM collisions
Algebra,Geometry, and Physics of momentum conservation axiom
Vector algebra of collisions
Matrix or tensor algebra of collisions
Deriving Energy Conservation Theorem
*Access Superball Collision Simulator
Link → http://www.uark.edu/ua/modphys/markup/BounceItWeb.html
 Part 2
Part 2 
(Ch. 3 to Ch. 5 of Unit 1)
Review of elastic Kinetic Energy ellipse geometry
The X2 Superball pen launcher
Perfectly elastic “ka-bong” velocity amplification effects (Faux-Flubber)
Geometry of X2 launcher bouncing in box
Independent Bounce Model (IBM)
Geometric optimization and range-of-motion calculation(s)
Integration of (V1,V2) data to space-time plots (y1(t),t) and (y2(t),t) plots
Integration of (V1,V2) data to space-space plots (y1, y2)
Example of (V1,V2) and (y1,y2) data for high mass ratios: m1/m2=49, 100,...
Multiple collisions calculated by matrix operator products
Matrix or tensor algebra of 1-D 2-body collisions
Ellipse rescaling-geometry and reflection-symmetry analysis
Rescaling KE ellipse to circle
How this relates to Lagrangian, l’Etrangian, and Hamiltonian mechanics in Ch. 12

(Ch. 3, Ch. 4, and Ch. 5 of Unit 1)
Review of (V1,V2) and (y1,y2) geometry and X2 launcher in box
Integration of (V1,V2) data to space-time plots (y1(t),t) and (y2(t),t) plots
Integration of (V1,V2) data to space-space plots (y1,y2)
Example of (V1,V2) and (y1,y2) data for high mass ratios: m1/m2=49, 100,...
Multiple collisions calculated by matrix operator products
Matrix or tensor algebra of 1-D 2-body collisions
“Mass-bang” matrix M, “Floor-bang” matrix F, “Ceiling-bang” matrix C.
Algebra and Geometry of “ellipse-Rotation” group product: R = C•M
Ellipse rescaling-geometry and reflection-symmetry analysis
Rescaling KE ellipse to circle
How this relates to Lagrangian, l’Etrangian, and Hamiltonian mechanics in Ch. 12
Reflections in the clothing store: “It’s all done with mirrors!”
Introducing hexagonal symmetry D6~C6v (Resulting for m1/m2=3)
Group multiplication and product table
Classical collision paths with D6~C6v (Resulting for m1/m2=3)
Solutions to Exercises 1.4.1 and 1.4.2
 Part 2
Part 2 
(Ch. 6, and Ch. 7 of Unit 1)
Review of (V1,V2)→(y1,y2) relations High mass ratio M1/m2 = 49
Force “field” or “pressure” due to many small bounces
Force defined as momentum transfer rate
The 1D-Isothermal force field F(y)=const./y and the 1D-Adiabatic force field F(y)=const./y3
Potential field due to many small bounces
Example of 1D-Adiabatic potential U(y)=const./y2
Physicist’s Definition F=-ΔU/Δy vs. Mathematician’s Definition F=+ΔU/Δy
Example of 1D-Isothermal potential U(y)=const. ln(y)
“Monster Mash”classical segue to Heisenberg action relations
Example of very very large M1 ball-wall(s) crushing a poor little m2
How m2 keeps its action
An interesting wave analogy: The “Tiny-Big-Bang”
[Harter, J. Mol. Spec. 210, 166-182 (2001)]
[Harter, Li IMSS (2012)]
Link → Quantum Revivals of Morse Oscillators and Farey-Ford Geometry - 2013
A lesson in geometry of fractions and fractals: Ford Circles and Farey Sums
Link → ["Fractions" - Lester. R. Ford, Am. Math. Monthly 45,586(1938)]
["On a Curious Property of Vulgar Fractions" - John Farey, Phil. Mag. 47, 385 (1816)]
(Ch. 7 and Ch. 8 of Unit 1)
(From Lect 5.) A lesson in geometry of fractions and fractals: Ford Circles and Farey Sums
Link → ["Fractions" - Lester. R. Ford, Am. Math. Monthly 45,586(1938)]
["On a Curious Property of Vulgar Fractions" - John Farey, Phil. Mag. 47, 385 (1816)]
Potential energy geometry of Superballs and related things
Thales geometry and “Sagittal approximation”
Geometry and dynamics of single ball bounce
Examples: (a) Constant force (like kidee pool) (b) Linear force (like balloon)
Some physics of dare-devil-divers
Non-linear force (like superball-floor or ball-bearing-anvil)
Geometry and dynamics of 2-ball bounce (again with feeling)
The parable of RumpCo. vs CrapCorp.
The story of USC pre-meds visiting Whammo Manufacturing Co.
Geometry and dynamics of 3-ball bounce
A story of Stirling Colgate (Palmolive) and core-collapse supernovae
Other bangings-on: The western buckboard and Newton’s balls
Crunch energy geometry of freeway crashes and related things
Crunch energy played backwards: This really is “Rocket-Science”
A Thales construction for momentum-energy

(Ch. 7 and Ch. 8 of Unit 1)
Potential energy geometry of Superballs and related things
Thales geometry and “Sagittal approximation” to force law
Geometry and dynamics of single ball bounce
(a) Constant force F=-k (linear potential V=kx )
Some physics of dare-devil diving 80 ft. into kidee pool
(b) Linear force F=-kx (quadratic potential V = ½kx2 (like balloon))
(c) Non-linear force (like superball-floor or ball-bearing-anvil)
Geometry and dynamics of 2-ball bounce
A parable of RumpCo. vs CrapCorp. (introducing 3-mass potential-driven dynamics)
A story of USC pre-meds visiting Whammo Manufacturing Co.
Geometry and dynamics of n-ball bounces
Analogy with shockwave and acoustical horn amplifier
Advantages of a geometric m1, m2, m3,… series
A story of Stirling Colgate (Palmolive) and core-collapse supernovae
(Leads to Sagittal potential analysis of 2, 3, and 4 body towers)
Many-body 1D collisions
Elastic examples: Western buckboard
Bouncing columns and Newton’s cradle
Inelastic examples: “Zig-zag geometry” of freeway crashes
Super-elastic examples: This really is “Rocket-Science”

Geometry of common power-law potentials
Geometric (Power) series
“Zig-Zag” exponential geometry
Projective or perspective geometry
Parabolic geometry of harmonic oscillator kr2/2 potential and -kr1 force fields
Coulomb geometry of -1/r-potential and -1/r2-force fields
Compare mks units of Coulomb Electrostatic vs. Gravity
Geometry of idealized “Sophomore-physics Earth”
Coulomb field outside Isotropic & Harmonic Oscillator (IHO) field inside
Contact-geometry of potential curve(s)
“Crushed-Earth” models: 3 key energy “steps” and 4 key energy “levels”
Earth matter vs nuclear matter:
Introducing the “neutron starlet” and “Black-Hole-Earth”
Introducing 2D IHO orbits and phasor geometry
Phasor “clock” geometry

(Ch. 9 and Ch. 11 of Unit 1)
Constructing 2D IHO orbits by phasor plots
Phasor “clock” geometry
Integrating IHO equations by phasor geometry
Constructing 2D IHO orbits using Kepler anomaly plots
Mean-anomaly and eccentric-anomaly geometry
Calculus and vector geometry of IHO orbits
A confusing introduction to Coriolis-centrifugal force geometry (Derived rigorously later in Ch. 12)
Some Kepler’s “laws” for central (isotropic) force F(r)
Angular momentum invariance of IHO: F(r)=-k·r with U(r)=k·r2/2 (Derived rigorously)
Angular momentum invariance of Coulomb: F(r)=-GMm/r2 with U(r)=-GMm·/r (Derived later in Unit 5)
Total energy E=KE+PE invariance of IHO: F(r)=-k·r (Derived rigorously)
Total energy E=KE+PE invariance of Coulomb: F(r)=-GMm/r2 (Derived later in Unit 5)
Brief introduction to matrix quadratic form geometry
Link → BoxIt simulation of U(2) orbits at http://www.uark.edu/ua/modphys/markup/BoxItWeb.html
Link → RelaWavity - IHO Elliptical orbits at http://www.uark.edu/ua/modphys/markup/RelaWavityWeb.html?plotType=1|0
Link → RelaWavity - IHO Ellipse Exegesis at http://www.uark.edu/ua/modphys/markup/RelaWavityWeb.html?plotType=1|1

(Ch. 11 and Ch. 12 of Unit 1)
Review of dual IHO elliptic orbits (Lecture 9)
Construction by Phasor-pair projection (with example of dual-ellipses)
Construction by Kepler anomaly projection
Introduction to dual matrix operator geometry
Quadratic form ellipse r•Q•r=1 vs. inverse form ellipse p•Q-1•p=1
Duality norm relations (r•p=1)
Q-Ellipse tangents r′ normal to dual Q-1-ellipse position p (r′•p=0=r•p′)
Operator geometric sequences and eigenvectors
Alternative scaling of matrix operator geometry
Vector calculus of tensor operation
Introduction to Lagrangian-Hamiltonian duality
Review of partial differential relations
Chain rule and order ∂2Ψ/∂x∂y= ∂2Ψ/∂y∂x symmetry
Duality relations of Lagrangian and Hamiltonian ellipse
Introducing the 1st (partial) differential equations of mechanics
Link → RelaWavity - IHO Elliptical orbits at http://www.uark.edu/ua/modphys/markup/RelaWavityWeb.html?plotType=1|0
Link → RelaWavity - IHO Ellipse Exegesis at http://www.uark.edu/ua/modphys/markup/RelaWavityWeb.html?plotType=1|1

(Ch. 12 of Unit 1 and Ch. 4-5 of Unit 7)
Scaling transformation between Lagrangian and Hamiltonian views of KE (Review of Lecture 10)
Introducing 1st Lagrange and Hamilton differential equations of mechanics (Review Of Lecture 10)
Introducing the Poincare´ and Legendre contact transformations
Geometry of Legendre contact transformation (Preview of Unit 8 relativistic quantum mechanics)
Example from thermodynamics
Legendre transform: special case of General Contact Transformation (Lights, Camera, ... ACTION!)
A general contact transformation from sophomore physics
Algebra-calculus development of “The Volcanoes of Io” and “The Atoms of NIST”
Intuitive-geometric development of ” ” ” and ” ” ”
Link → CoulIt web app at http://www.uark.edu/ua/modphys/markup/CoulItWeb.html

(Ch. 12 of Unit 1 and Ch. 1-5 of Unit 2 and Ch. 1-5 of Unit 3)
Quick Review of Lagrange Relations in Lectures 9-11
Using differential chain-rules for coordinate transformations
Polar coordinate example of Generalized Curvilinear Coordinates (GCC)
Getting the GCC ready for mechanics: Generalized velocity and Jacobian Lemma 1
Getting the GCC ready for mechanics: Generalized acceleration and Lemma 2
How to say Newton’s “F=ma” in Generalized Curvilinear Coords.
Use Cartesian KE quadratic form KE=T=v•M•v/2 and F=M•a to get GCC force
Lagrange GCC trickery gives Lagrange force equations
Lagrange GCC trickery gives Lagrange potential equations (Lagrange 1 and 2)
GCC Cells, base vectors, and metric tensors
Polar coordinate examples: Covariant Em vs. Contravariant Em
Covariant metric gmn vs. Invariant δmn vs. Contravariant metric gmn
Lagrange prefers Covariant gmn with Contravariant velocity
GCC Lagrangian definition
GCC “canonical” momentum pm definition
GCC “canonical” force Fm definition/p>
Coriolis “fictitious” forces (… and weather effects)

(Unit 1 Ch. 12, Unit 2 Ch. 2-7, Unit 3 Ch. 1-3)
Review of Lectures 9-12 procedures:
Lagrange prefers Covariant metric gmn with Contravariant velocity ![]()
Hamilton prefers Contravariant metric gmn with Covariant momentum pm
Deriving Hamilton’s equations from Lagrange’s equations
Expressing Hamiltonian H(momentum pm,qn) using gmn and covariant momentum pm
Polar-coordinate example of Hamilton’s equations
Hamilton’s equations in Runga-Kutta (computer solution) form
Examples of Hamiltonian mechanics in effective potentials
Isotropic Harmonic Oscillator in polar coordinates and effective potential (Simulation)
Coulomb orbits in polar coordinates and effective potential (Simulation)
Parabolic and 2D-IHO orbital envelopes
Clues for future assignment _ (Simulation)
Examples of Hamiltonian mechanics in phase plots
1D Pendulum and phase plot (Simulation)
1D-HO phase-space control (Simulation)
Link → CoulIt - IHO, Coulomb, Parabolic and 2D-IHO orbital envelopes at http://www.uark.edu/ua/modphys/markup/CoulItWeb.html
Link → Pendulum - Treatment of 1D pendulum at http://www.uark.edu/ua/modphys/markup/PendulumWeb.html
Link → Cycloidulum - IHO Ellipse Exegesis at http://www.uark.edu/ua/modphys/markup/CycloidulumWeb.html
Link → JerkIt - Driven 1D motion at http://www.uark.edu/ua/modphys/markup/JerkItWeb.html

(Unit 1 Ch. 12, Unit 2 Ch. 2-7, Unit 3 Ch. 1-3, Unit 7 Ch. 1-2)
Review of Lecture 12 relations
Examples of Hamiltonian mechanics in phase plots
1D Pendulum and phase plot (Simulation)
1D-HO phase-space control (Simulation of “Catcher in the Eye”)
Exploring phase space and Lagrangian mechanics more deeply
A weird “derivation” of Lagrange’s equations
Poincare identity and Action, Jacobi-Hamilton equations
How Classicists might have “derived” quantum equations
Huygen’s contact transformations enforce minimum action
How to do quantum mechanics if you only know classical mechanics
(“Color-Quantization” simulations: Davis-Heller “Color-Quantization” or “Classical Chromodynamics”)

(Ch. 10 of Unit 1)
|
1. The Story of e (A Tale of Great $Interest$) How good are those power series? Taylor-Maclaurin series, imaginary interest, and complex exponentials 2. What good are complex exponentials? Easy trig Easy 2D vector analysis Easy oscillator phase analysis Easy rotation and “dot” or “cross” products 3. Easy 2D vector calculus Easy 2D vector derivatives Easy 2D source-free field theory Easy 2D vector field-potential theory 4. Riemann-Cauchy relations (What’s analytic? What’s not?) Easy 2D curvilinear coordinate discovery Easy 2D circulation and flux integrals Easy 2D monopole, dipole, and 2n-pole analysis Easy 2n-multipole field and potential expansion Easy stereo-projection visualization Cauchy integrals, Laurent-Maclaurin series 5. Mapping and Non-analytic 2D source field analysis |
1. Complex numbers provide "automatic trigonometry" 2. Complex numbers add like vectors. 3. Complex exponentials Ae-iωt track position and velocity using Phasor Clock. 4. Complex products provide 2D rotation operations. 5. Complex products provide 2D “dot”(•) and “cross”(x) products. 6. Complex derivative contains “divergence”(∇•F) and “curl”( ∇xF) of 2D vector field 7. Invent source-free 2D vector fields [∇•F=0 and ∇xF=0] 8. Complex potential φ contains “scalar”( F= ∇Φ) and “vector”( F=∇xA) potentials 9. Complex potentials define 2D Orthogonal Curvilinear Coordinates (OCC) of field 10. Complex integrals ∫ f(z)dz count 2D “circulation”( ∫F•dr) and “flux”( ∫Fxdr) 11. Complex integrals define 2D monopole fields and potentials 12. Complex derivatives give 2D dipole fields 13. More derivatives give 2D 2N-pole fields… 14. ...and 2N-pole multipole expansions of fields and potentials... 15. ...and Laurent Series... 16. ...and non-analytic source analysis. |

(Ch. 10 of Unit 1)
|
1. The Story of e (A Tale of Great $Interest$) How good are those power series? Taylor-Maclaurin series, imaginary interest, and complex exponentials 2. What good are complex exponentials? Easy trig Easy 2D vector analysis Easy oscillator phase analysis Easy rotation and “dot” or “cross” products 3. Easy 2D vector calculus Easy 2D vector derivatives Easy 2D source-free field theory Easy 2D vector field-potential theory 4. Riemann-Cauchy relations (What’s analytic? What’s not?) Easy 2D curvilinear coordinate discovery Easy 2D circulation and flux integrals Easy 2D monopole, dipole, and 2n-pole analysis Easy 2n-multipole field and potential expansion Easy stereo-projection visualization Cauchy integrals, Laurent-Maclaurin series 5. Mapping and Non-analytic 2D source field analysis |
1. Complex numbers provide "automatic trigonometry" 2. Complex numbers add like vectors. 3. Complex exponentials Ae-iωt track position and velocity using Phasor Clock. 4. Complex products provide 2D rotation operations. 5. Complex products provide 2D “dot”(•) and “cross”(x) products. Lecture 16 Thur. 10.16.14 starts here ⤵ 6. Complex derivative contains “divergence”(∇•F) and “curl”( ∇xF) of 2D vector field 7. Invent source-free 2D vector fields [∇•F=0 and ∇xF=0] 8. Complex potential φ contains “scalar”( F= ∇Φ) and “vector”( F=∇xA) potentials The half-nʼ-half results: (Riemann-Cauchy Derivative Relations) 9. Complex potentials define 2D Orthogonal Curvilinear Coordinates (OCC) of field 10. Complex integrals ∫ f(z)dz count 2D “circulation”( ∫F•dr) and “flux”( ∫Fxdr) 11. Complex integrals define 2D monopole fields and potentials 12. Complex derivatives give 2D dipole fields 13. More derivatives give 2D 2N-pole fields… 14. ...and 2N-pole multipole expansions of fields and potentials... 15. ...and Laurent Series... 16. ...and non-analytic source analysis. |

(Ch. 1-3 of Unit 2 and Unit 3)
The trebuchet (or ingenium) and its cultural relevancy (3000 BCE to 21st See Sci. Am. 273, 66 (July 1995))
The medieval ingenium (9th to 14th century) and modern re-enactments
Human kinesthetics and sports kinesiology
Cartesian to GCC transformations (Mostly Unit 2.)
Jacobian relations
Kinetic energy calculation
Dynamic metric tensor γmn
Geometric and topological properties of GCC transformations (Mostly Unit 3.)
Multivalued functionality and connections
Covariant and contravariant relations
Metric tensors

(Ch. 1-5 of Unit 2 and Unit 3)
Review of Lagrangian equation derivation (Elementary trebuchet) (Mostly Unit 2.)
Coordinate geometry, kinetic energy, and dynamic metric tensor γmn
Force, work, and acceleration
Lagrangian force equation
Canonical momentum and γmn tensor
Equations of motion and force analysis (Mostly Unit 2.)
Forces: total, genuine, potential, and/or fictitious
Lagrange equation forms
Riemann equation forms
2nd-guessing Riemann? (More like Unit 3.)

(Ch. 5-9 of Unit 2)
Review of Hamiltonian equation derivation (Elementary trebuchet)
Hamiltonian definition from Lagrangian and γmn tensor
Hamilton’s equations and Poincare invariant relations
Hamiltonian expression and contravariant γmn tensor
Hamiltonian energy and momentum conservation and symmetry coordinates
Coordinate transformation helps reduce symmetric Hamiltonian
Free-space trebuchet kinematics by symmetry
Algebraic approach
Direct approach and Superball analogy
Trebuchet vs Flinger and sports kinematics
Many approaches to Mechanics
(Ch. 4-7 of Unit 3)
Covariant derivative and Christoffel Coefficients Γij;k and Γij;k
Christoffel g-derivative formula
What’s a tensor? What’s not?
General Riemann equations of motion (No explicit t-dependence and fixed GCC)
Example of Riemann-Christoffel forms in cylindrical polar OCC (q1 = ρ, q2 = φ, q3 = z)
Separation of GCC Equations: Effective Potentials
Small radial oscillations
Cycloid vs Pendulum

(Ch. 2.8 of Unit 2)
Charge mechanics in electromagnetic fields
Vector analysis for particle-in-(A,Φ)-potential
Lagrangian for particle-in-(A,Φ)-potential
Hamiltonian for particle-in-(A,Φ)-potential
Crossed E and B field mechanics
Classical Hall-effect and cyclotron orbits
Vector theory vs. complex variable theory
Mechanical analog of cyclotron and FBI rule

(Ch. 2.8 of Unit 2)
Separation of GCC Equations: Effective Potentials
Small radial oscillations
2D Spherical pendulum or “Bowl-Bowling”
Cycloidal ruler & compass geometry
Cycloid as brachistichrone with various geometries
Cycloid as tautochrone
Cycloidulum vs Pendulum
Cycloidal geometry of flying levers
Practical poolhall application

(Ch. 9 of Unit 3)
Some Ways to do constraint analysis
Way 1. Simple constraint insertion
Way 2. GCC constraint webs
Find covariant force equations
Compare covariant vs. contravariant forces
Other Ways to do constraint analysis
Way 3. OCC constraint webs
Preview of atomic-Stark orbits
Classical Hamiltonian separability
Way 4. Lagrange multipliers
Lagrange multiplier as eigenvalues
Multiple multipliers
“Non-Holonomic” multipliers

(Ch. 1 of Unit 4 11.14.13)
1D forced-damped-harmonic oscillator equations and Green’s function solutions
Linear harmonic oscillator equation of motion.
Linear damped-harmonic oscillator equation of motion.
Frequency retardation and amplitude damping.
Figure of oscillator merit (the 5% solution 3/Γ and other numbers)
Linear forced-damped-harmonic oscillator equation of motion.
Phase lag and amplitude resonance amplification
Figure of resonance merit: Quality factor q=ω0/2Γ
Properties of Green’s function solutions and their mathematical/physical behavior
Transient solutions vs. Steady State solutions
Complete Green’s SolutionGreen’s Solution for the FDHO (Forced-Damped-Harmonic Oscillator)
Quality factors: Beat, lifetimes, and uncertainty
Approximate Lorentz-Green’s Function for high quality FDHO (Quantum propagator)
Common Lorentzian (a.k.a. Witch of Agnesi)
(Ch. 2-4 of Unit 4 11.19.13)
Damped-Harmonic Review: Green’s Solution for the FDHO (Forced-Damped-Harmonic Oscillator)
Beat, lifetimes, and quality factor q = ω0/2Γ and Q = υ0/2Γ = q/2π
Review: Approximate Lorentz-Green’s Function for high quality FDHO (Quantum propagator)
Common Lorentzian (a.k.a. Witch of Agnesi) and geometry
2D harmonic oscillator equations
Lagrangian and matrix forms
Reciprocity symmetry
2D harmonic oscillator equation eigensolutions
Geometric method
Matrix-algebraic method with example M = 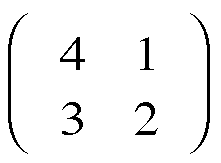
Secular eq., Hamilton-Cayley eq., Idempotent projectors, (how eigenvalues⇒eigenvectors)
Spectral decomposition and P-operator expansions (how projectors⇒eigensolutions)
2D-HO eigensolution example with bilateral (B-Type) symmetry
Mixed mode beat dynamics and fixed π/2 phase
2D-HO eigensolution example with asymmetric (A-Type) symmetry
Initial state projection, mixed mode beat dynamics with fluid phase
ANALOGY: 2-State Schrodinger: iħ∂t|Ψ(t)〉=H|Ψ(t)〉 versus Classical 2D-HO: ∂2tx=-K•x
Hamilton-Pauli spinor symmetry (ABCD-Types)
(Ch. 2-4 of Unit 4 Ch. 6-7 of Unit 6)
Review: 2D harmonic oscillator equations with Lagrangian and matrix forms
ANALOGY: 2-State Schrodinger: iħ∂t|Ψ(t)〉=H|Ψ(t)〉 versus Classical 2D-HO: ∂2tx=-K•x
Hamilton-Pauli spinor symmetry ( σ-expansion in ABCD-Types) H=ωμσμ
Derive σ-exponential time evolution (or revolution) operator U = e-iHt = e-iσµωµt
Spinor arithmetic like complex arithmetic
Spinor vector algebra like complex vector algebra
Spinor exponentials like complex exponentials ("Crazy-Thing"-Theorem)
Geometry of evolution (or revolution) operator U = e-iHt = e-iσµωµt
The "mysterious" factors of 2 (or 1/2): 2D Spinor vs 3D Spin Vector space
2D Spinor vs 3D vector rotation
NMR Hamiltonian: 3D Spin Moment m in B field
Euler's state definition using rotations R(α,0,0), R(0,β,0),and R(0,0,γ)
Spin-1 (3D-real vector) case
Spin-1/2 (2D-complex spinor) case
3D-real Stokes Vector defines 2D-HO polarization ellipses and spinor states
Asymmetry SA=SZ, Balance SB =SX, and Chirality SC =SY
Polarization ellipse and spinor state dynamics
The "Great Spectral Avoided-Crossing" and A-to-B-to-A symmetry breaking
See also: QTCA Lect. 9(2.12) p.61-103 for polarization ellipsometry

(Ch. 7-8 of Unit 4 12.02.14)
Two Kinds of Resonance: Linear-additive vs. Nonlinear-multiplicative (Parametric resonance)
Coupled rotation and translation (Throwing revisited: trebuchet, atlatl, etc.)
Schrodinger wave equation related to Parametric resonance dynamics
Electronic band theory and analogous mechanics
Wave resonance in cyclic symmetry
Harmonic oscillator with cyclic C2 symmetry
C2 symmetric (B-type) modes
Harmonic oscillator with cyclic C3 symmetry
C3 symmetric spectral decomposition by 3rd roots of unity
Resolving C3 projectors and moving wave modes
Dispersion functions and standing waves
C6 symmetric mode model:Distant neighbor coupling
C6 spectra of gauge splitting by C-type symmetry(complex, chiral, coriolis, current, …)
CN symmetric mode models: Made-to order dispersion functions
Quadratic dispersion models: Super-beats and fractional revivals
Phase arithmetic
Algebra and geometry of resonant revivals: Farey Sums and Ford Circles
Relating CN symmetric H and K matrices to differential wave operators

(Ch. 2-4 of Unit 5 12.04.14)
Review: “3steps from Hell” (Lect. 7 Ch. 9 Unit 1)
Orbits in Isotropic Harmonic Oscillator and Coulomb Potentials
Effective potentials for IHO and Coulomb orbits
Stable equilibrium radii and radial/angular frequency ratios
Classical turning radii and apogee/perigee parameters. ← (A mysterious similarity appears)
Polar coordinate differential equations ← (A mysterious similarity appears)
Quadrature integration techniques
Detailed orbital functions ← (A mysterious similarity appears)
Relating orbital energy-momentum to conic-sectional orbital geometry
Kepler equation of time and phase geometry
Geometry and Symmetry of Coulomb orbits
Detailed elliptic geometry
Detailed hyperbolic geometry

(Ch. 2-4 of Unit 5 12.11.14)
Rutherford scattering and differential scattering cross-sections
Parabolic “kite” and envelope geometry
Eccentricity vector ε and (ε,λ)-geometry of orbital mechanics
ε-vector and Coulomb r-orbit geometry
Review and connection to standard development
ε-vector and Coulomb p=mv geometry
ε-vector and Coulomb p=mv algebra
Example with elliptical orbit
Analytic geometry derivation of ε-construction
Algebra of ε-construction geometry
Connection formulas for (a,b) and (ε,λ) with (γ,R)

(Ch. 2-4 of Unit 5)
Eccentricity vector ε and (ε,λ)-geometry of orbital mechanics ← Review of lectures 28 and 29
ε-vector and Coulomb r-orbit geometry ←
Review and connection to standard development ←
ε-vector and Coulomb p=mv geometry ←
Example with elliptical orbit ←
Analytic geometry derivation of ε-construction
Algebra of ε-construction geometry
Connection formulas for (a,b) and (ε,λ) with (γ,R)
Ruler & compass construction of ε-vector and orbits
(R=-0.375 elliptic orbit)
(R=+0.5 hyperbolic orbit)
Properties of Coulomb trajectory families and envelopes
Graphical ε-development of orbits
Launch angle fixed-Varied launch energy
Launch energy fixed-Varied launch angle
Launch optimization and orbit family envelopes
(Ch. 2-7 of Unit 6)
2-Particle orbits
Ptolemetric or LAB view and reduced mass
Copernican or COM view and reduced coupling
2-Particle orbits and scattering: LAB-vs.-COM frame views
Ruler & compass construction (or not)
Rotational equivalent of Newton’s F=dp/dt equations: N=dL/dt
How to make my boomerang come back
The gyrocompass and mechanical spin analogy
Rotational momentum and velocity tensor relations
Quadratic form geometry and duality (again)
Angular velocity ω-ellipsoid vs. angular momentum L-ellipsoid
Lagrangian ω-equations vs. Hamiltonian momentum L-equation
Rotational Energy Surfaces (RES) and Constant Energy Surfaces (CES)
Symmetric, asymmetric, and spherical-top dynamics (Constant L)
BOD-frame cone rolling on LAB frame cone
Deformable spherical rotor RES and semi-classical rotational states and spectra