

| Text Colors |

Sketch of modern molecular spectroscopy
Example of 16μm spectra of CF4 1996 AMOP Handbook from Springer
Example of 16μm spectra of SF6 2005 AMOP Handbook
Example of ??μm spectra of C60 2018? AMOP Handbook
Units of frequency (Hz), wavelength (m), and energy (eV)
Spectral windows in atmosphere due to molecules
Simple molecular-spectra models
2-well tunneling, Bohr mass-on-ring, 1D harmonic oscillator, Coulomb PE models
More advanced molecular-spectra models (Using symmetry-group theory)
2-state U(2)-spin tunneling models
3D R(3)-rotor and D-function lab-body wave models
2D harmonic oscillator and U(2) 2nd quantization
Bohr Mass-On-a-Ring (model of rotation) and related ∞-Square Well (model of quantum dots)
Quantum levels of ∞-Square well and Bohr rotor
Example of CO2 rotational (υ=0)⇔(υ=1)bands
Quantum dynamics of ∞-Square well and Bohr rotor: What makes that “dipole”spectra?
Quantum dynamics of Double-well tunneling: Cheap models of NH3 inversion doublet
Quantum “blasts” of strongly localized ∞-well or rotor waves: A lesson in quantum interference
Wavepacket explodes! (Then revives)

Sketch of modern molecular spectroscopy
Example of 16μm spectra of CF4 1996 AMOP Handbook from Springer
Example of 16μm spectra of SF6 2005 AMOP Handbook
Example of ??μm spectra of C60 2018? AMOP Handbook
Units of frequency (Hz), wavelength (m), and energy (eV)
Spectral windows in atmosphere due to molecules
Simple molecular-spectra models
2-well tunneling, Bohr mass-on-ring, 1D harmonic oscillator, Coulomb PE models
More advanced molecular-spectra models (Using symmetry-group theory)
2-state U(2)-spin tunneling models
3D R(3)-rotor and D-function lab-body wave models
2D harmonic oscillator and U(2) 2nd quantization
Bohr Mass-On-a-Ring (model of rotation) and related ∞-Square Well (model of quantum dots)
Quantum levels of ∞-Square well and Bohr rotor
Example of CO2 rotational (υ=0)⇔(υ=1)bands
Quantum dynamics of ∞-Square well and Bohr rotor: What makes that “dipole”spectra?
Quantum dynamics of Double-well tunneling: Cheap models of NH3 inversion doublet
Quantum “blasts” of strongly localized ∞-well or rotor waves: A lesson in quantum interference
Wavepacket explodes! (Then revives)
Symmetry group representations
AMOP Hamiltonian matrices
AMOP wave functions and eigensolutions

𝒢 = C2 = Cyclic (or Circle) group of order 2
Basic Projection operators GThLect.4 p.31-46
C2 spectral resolution for group C2 GThLect.6 p.17
C2 spectral resolution for 2D oscillator GThLect.6 p.33
C2 beat dynamics for 2D oscillator GThLect.6 p.35-46
U(2) beat phase dynamics for 2D oscillator GThLect.6 p.52-56
𝒢 = C3 = Cyclic (or Circle) group of order 3
C3 Basic group representation theory. GThLect.11 p6-12.
C3 group spectral resolution. GThLect.11 p14-27
C3 Operator/State-Ortho-completeness GThLect.11 p29-38
C3 Wavefunction bra-kets GThLect.11 p40-45.
C3 quantum number Mod-3 formulae GThLect.11 p47-52.
C3 character or irrep tables GThLect.11 p54-58.
C3 wave dispersion functions GThLect.11 p60-68.
Moving vs standing waves p71-73
Radial vs transverse waves p71-73
𝒢 = C6 = Cyclic (or Circle) group of order 6
1st Step: Find C6 symmetric H by C6 product table of regular reps and coupling params{r0,r1…r5}GThLect12 p3-9
2nd Step: Find H eigenfunctions by spectral resolution of C6 ={1=r0,r1,r2,r3,r4,r5}GThLect12 p11-16
Character tables of C2, C3, C4, C5,…. C144 GThLect12 p18-24
3rd Step: Dispersion functions and eigenvalues for various coupling parameter sets GThLect12 p27-30
Ortho-complete eigenvalue/parameters p32-38
Gauge shifting complex coupling p40-48
Bohr-Schrodinger dispersion p49-51

Memoriam: Charles H. Townes 1916-2015 and his famous 2-state system: NH3 maser in 1955
Earlier 2-state systems: 1863 John Stokes optical polarization, 1954 Rabi, Ramsey, and Schwinger NMR (MRI)
ANALOGY: (1) Classical 2-state motion (∂/∂t)2x=-K·x vs (2) Quantum 2-state motion ih(∂/∂t)Ψ= H·Ψ
Hamilton-Pauli spinor symmetry and σ-expansion of H=ωμσμ= ωAσA + ωBσB + ωCσC + ω0σ0
ABCD Time evolution operator U(t)= e-iHt ; its evaluation and visualization
ABCD symmetry operator {σA,σB,σC} product algebra for spinor-vector operators σa=σ·a
Spinor-vector operator products (σ· a)(σ· a)
Crazy-Thing Theorem: e = 1<strong>cosΘ - iσasinΘ
U(2) transformation matrices and related R(3) rotations in ABC-space
Mysterious factors of 2 or ½ on 2D spinors or 3D vectors
2D {↑, ↓} spinor space ½ as fast as 3D {ABC} spin-vectors
Hamiltonian for NMR: 3D Spin Moment Vector m=(mx, my, mz,) in field B=(Bx, By, Bz)
State coordinates using Euler-angle rotations R(α,0,0), R(0,β,0), and R(0,0,γ)
Spin-1 (3D-real vector) case
Spin-1/2 (2D-complex spinor) case
The ABC’s of U(2) dynamics-Archetypes
Asymmetric-Diagonal A-Type motion
Bilateral-Balanced B-Type motion
Circular-Coriolis… C-Type motion

Relating Euler and Darboux angles to U(2) phasor coordinates x1+ip1 and x2+ip2.
Derivation of Euler-to-Darboux and Darboux-to-Euler conversion formulae, Test of formulae.
Darboux R[ϕϑΘ] spin-½ rotation Θ=0 to 4π for fixed [ϕϑ] “Real-world” 4π spin-½ behavior.
Review of U(2) dynamics: H=AσZ (A-Type), H=BσX (B-Type), H=CσY (C-Type).
U(2) dynamics of mixed-Types: H=AσZ+BσX (AB-Type), Avoided crossing around Dirac-point.
H=AσZ+BσX+CσY (ABC-Type), Invariant Tori in (x1,p1,x2,p2)-space.
Conventional amplitude-phase-(A1,A2,ω,ρl) labeling of optical polarization
To find U(2) eigenstates: Match H axis-angles[ϕϑΘ] to S Euler angles (αβγ) A-Type (αA,βA,γA),
Fast mode of elliptic polarization vs Slow mode (or no-mode) of orthogonal elliptic orbit
Euler angle labeling of optical polarization C-Type (αC,βC,γC) vs A-Type (αA,βA,γA),

G = U(2) product R[Θ]R[Θ′]=R[Θ′′′] algebra (It’s all done with σμ spinors)
Jordan-Pauli identity: U(2) product algebra of spinor σμ-operators
U(2) “Crazy-Thing” forms do products R[Θ]R[Θ′]=R[Θ′′′] algebraically
G = U(2) product R[Θ]R[Θ′]=R[Θ′′′] by geometry (It’s all done with σμ mirrors)
Mirror reflections by σμ-operators make rotations The famous Clothing Store Mirror
Hamilton-turns do products R[Θ]R[Θ′]=R[Θ′′′] geometrically
Hamilton-turn slide rule and sundial U(2) products and (α,β,γ)-[ϕ,ϑ,Θ] conversions
Finite group products by turns or by group link diagrams D3 example. Oh example
G = U(2) class transformation R[Θ]R[Θ′]R[Θ]-1=R[Θ′′′] geometry
Group classes and subgroup cosets
U(2) density operator ρ and [ρ,H] mechanics
Density mechanics compared to spin vector S rotated by crank vector Θ=Ωt
Bloch equation: 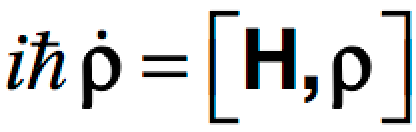

Factoring 1D-HO Hamiltonian H=p2+x2
Creation-Destruction a†a algebra of U(1) operators
Eigenstate creationism (and destructionism)
Vacuum state |0>
1st excited state |1>, |2>, ...
Normal ordering for matrix calculation (creation a† on left, destruction a on right)
Commutator derivative identities
Binomial expansion identities
Matrix 〈ana†n〉 calculations
Number operator and Hamiltonian operator
Expectation values of position, momentum, and uncertainty for eigenstate ⏐n〉
Harmonic oscillator beat dynamics of mixed states
Oscillator coherent states (“Shoved” and “kicked” states)
Translation operators vs. boost operators
Time evolution of coherent state
Properties of coherent state and “squeezed” states

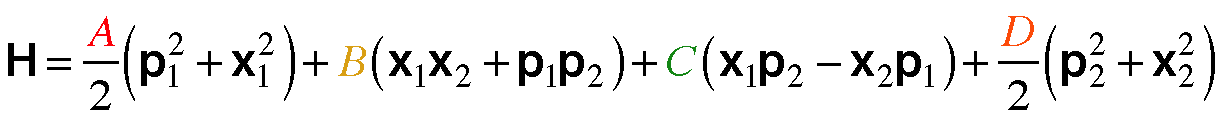
|
2D-Oscillator basic states and operations Commutation relations Bose-Einstein symmetry vs Pauli-Fermi-Dirac (anti)symmetry Anti-commutation relations |
Mostly Notation and Bookkeeping |
Two-dimensional (or 2-particle) base states: ket-kets and bra-bras
Outer product arrays
Entangled 2-particle states
Two-particle (or 2-dimensional) matrix operators
U(2) Hamiltonian and irreducible representations
2D-Oscillator states and related 3D angular momentum multiplets
R(3) Angular momentum generators by U(2) analysis
Angular momentum raise-n-lower operators s+ and s-
SU(2)⊂U(2) oscillators vs. R(3)⊂O(3) rotors

Review of angular momentum
1. Raise-n-lower operators S+ and S-
2. Commutation relations
3. SU(2)⊂U(2) oscillators vs. R(3)⊂O(3) rotors
Angular momentum magnitude and ΘJm-uncertainty cone polar angles
Generating higher-j representations DJmn of R(3) rotation and U(2) from spinor D1/2 irreps
Evaluating DJmn representations
Applications of DJmn representations
Atomic wave functions. DLm0 ~YLm Spherical harmonics
DL=1m0 ~YLm p-waves
DL=2m0 ~Y2m d-waves
DL00 ~PL Legendre waves
Molecular DJmn wave functions in“Mock-Mach” lab-vs-body state space |Jmn〉
Pjmn projector and DJmn(α,β,γ) wave function
DJmn transform R(α,β,γ)|Jmn〉=Σm'DJm'n(α,β,γ)|Jm'n〉in lab-space, R(α,β,γ) in body-space.
D2mn transform in lab-space (Generalized Stern-Gerlach beam polarization)
ΘJm-cone properties of lab transforms: J=20, J=10, J=30.
ΘJm-analysis of high J atomic beams
ΘJm-properties of high J molecular lab-vs-body states |Jm'n〉
Rotor Hamiltonian H = AJx2+BJy2+CJz2 made of scalar T00 or tensor Tq2 operators
Rotational Energy Surfaces (RE or RES) of symmetric rotor and eigensolutions
Rotational Energy Surfaces (RE or RES) of asymmetric rotor (for following class)

Review 1. Review of angular momentum cone geometry
Review 2. Review of Rotational Energy Surfaces (RE or RES) of symmetric rotor and eigensolutions
Review 3. Review of RES and Multipole Tqk tensor expansions
Energy levels and RES of symmetric rotors: prolate vs. oblate cases
RES of prolate and oblate rotor vs. asymmetric rotor (Introducing D2 symmetry labels)
Asymmetric rotor is not Unsymmetric rotor
Polygonal algebra & geometry of U(2)⊃CN character spectral function
Algebra of geometric series. Geometry of algebraic series
Molecular (2l+1)-multiplet D2-level splitting Examples: l=1, 2, 3,...
j,m,n formulas for momentum operator matrix elements:Hamiltonian matrix for asymmetric rotor
(J=1)-Matrix for A=1, B=2, C=3. (J=2)-Matrix for A=1, B=2, C=3
Completing diagonalization from new D2 basis:
J=2 example of asymmetry levels. J=20 example of asymmetry levels
Examples of Group⊃Sub-group correlation

RES and Multipole Tqk tensor expansions
RES and matrix representation of multipole Tqk tensor H-expansions
What tensors go in tetrahedral (Td) or octahedral (Oh) free-rotor Hamiltonia H ?
4th-rank [k=4] multipole terms
Oh-symmetric function and Oh operator T{4}
RES and matrix irreps of Oh multipole Tq[4] and Tq[2,2] tensor H-expansions
Matrix DT1, DT2, DE, DA2, and DA1, irreducible representations (irreps) of O
Finding Oh group products. Examples: Rz1=Rz or Rzi6=r3 or i6Rz=r1
DT1 irreps derived visually using unit vectors {x,y,z} of p-wave Dl=1{x,y,z}
DT2 irreps derived from standing d-wave Dl=2{x,y,z}. DE irrep tensor basis
Summary of irrep characters χT1, χT2, χE, χA2, and χA1 of O
R(3)⊃O character analysis. O⊃D4⊃D2 and O⊃D4⊃C4 level correlations s
Applications of Group⊃Sub-group correlation
Comparing Octahedral and Asymmetric rotor states and level clusters at high J
Appendix: O⊃D4⊃D2 irrep table very similar to our irreps on p.48

32 crystal point symmetries: 16 Abelian (commutative) and 16 non-Abelian groups
Smallest non-Abelian symmetry: 3-C2-axis D3 vs. 3-Cv-plane C3v isomorphic to permutation-S3
Relating C2-180°rotations Rz, Cv-plane reflections σz, and inversion I operators
Deriving D3 ~ C3v products by group definition ⏐g〉=g⏐1〉 of position ket ⏐g〉
Deriving D3 ~ C3v equivalence transformations and classes
Non-commutative symmetry expansion and Global-Local solution
Global vs Local symmetry and Mock-Mach principle
Global vs Local matrix duality for D3
Global vs Local symmetry expansion of D3 Hamiltonian
Group theory and algebra of D3 Center (Class algebra)
Self-symmetry (Normalizer). Lagrange Coset Theorem for classes
1st-Stage spectral decomposition of “Group-table” Hamiltonian of D3 symmetry
All-commuting operators κk All-commuting projectors P(α)
D3-invariant irep characters χk(α) Invariant numbers: Centrum, Rank, and Order
2nd-Stage spectral decompositions of global/local D3
Subgroup chains D3⊃C2 and D3⊃C3 split class projectors ...and classes
3rd-Stage spectral decomposition of ALL of D3 ...and of Hamiltonian H
GLOBAL vs LOCAL symmetry of states ...and group H parameters{r,i1,i2,i3}

Review 1. Global vs Local symmetry and Mock-Mach principle
Review 2. LAB-BOD (Global-Local) mutually commuting representations of D3~C3v
Review 3. Global vs Local symmetry expansion of D3 Hamiltonian
Review 4. 1st-Stage: Spectral resolution of D3 Center (All-commuting class projectors and characters)
Review 5. 2nd-Stage: D3⊃C2 or D3⊃C3 sub-group-chain projectors split class projectors PE=PE11+PE22 with:1=ΣPαjj
Review 6. 3rd-Stage: g=1·g·1 trick gives nilpotent projectors PE12=(PE21)† and Weyl g-expansion: g=ΣDαij(g)Pαij .
Deriving diagonal and off-diagonal projectors PEab and ireps DEab
Comparison: Global vs Local ⏐g〉-basis versus Global vs Local ⏐P(μ)〉-basis
General formulae for spectral decomposition (D3 examples)
Weyl g-expansion in irep Dμjk(g) and projectors Pμjk
Pμjk transforms right-and-left
Pμjk -expansion in g-operators: Inverse of Weyl form
D3 Hamiltonian and D3 group matrices in global and local ⏐P(μ)〉-basis
P(μ)〉-basis D3 global-g matrix structure versus D3 local-g matrix structure
Local vs global x-symmetry and y-antisymmetry D3 tunneling band theory
Ortho-complete D3 parameter analysis of eigensolutions
Classical analog for bands of vibration modes

Review: H-matrix Global vs Local symmetry
Molecular vibration K-matrix symmetry analogous to quantum H-matrix
Molecular K-matrix construction
D3⊃C2(i3) local-symmetry K-matrix eigensolutions
D3-direct-connection K-matrix eigenstates mix local symmetry
D3⊃C3(r±1) moving-wave local symmetry K-matrix “Coriolis” eigensolutions
Applied symmetry reduction and splitting
Subduced irep Dα(D3)↓C2 = d02⊕d12⊕.. correlation
Subduced irep Dα(D3)↓C3 = d03⊕d13⊕.. correlation
Spontaneous symmetry breaking and clustering: Frobenius Reciprocity and band structure
Induced rep da(C2)↑D3 = Dα⊕Dβ⊕.. correlation
Induced rep da(C3)↑D3 = Dα⊕Dβ⊕.. correlation
D6 symmetry and Hexagonal Bands
Cross product of the C2 and D3 characters gives all D6 = D3 ×C2 characters and ireps
D6 Band structure and related Global vs Local induced representations, D4 example
U(12)-Supersymmetry

Review: Global vs Local symmetry and Mock-Mach principle
Pμ in χμ-terms of κg κg in χμ*-terms of Pμ Irep frequncy fμ in χμ*-terms of TraceR(g)
Introducing octahedral/ tetrahedral symmetry Oh⊃O~Td⊃T : relating D4⊃C4 and D3⊃C3
Octahedral-cubic O symmetry and group operations, O slide-rule
Tetrahedral symmetry leads to Icosahedral
Octahedral groups Oh⊃O~Td⊃T and its large subgroups. Oh slide-rule
Octahedral O and spin-O⊂U(2) nomograms
Tetrahedral T class algebra minimal equations centrum projectors and characters
Octahedral O class algebra minimal equations centrum projectors and characters
Characters of full Octahedral symmetry Oh=O×CI=O×{1,I}
Octahedral Oh⊃O⊃CI subgroup correlations
Octahedral subgroup correlation Oh⊃O⊃D4 Oh⊃O⊃D4⊃C4 and level-splitting
Comparing O⊃C4 and O⊃C3 and O⊃C2
R(3)⊂O(3)⊃Oh⊃O character analysis: Crystal field splitting p, d, f,...orbitals
Cluster structure in SF6 16um spectra. Analogy with D6 band gap structure
Global vs Local External LAB splitting vs Internal BODY clustering
Detailed superfine structure for A1T1E cluster preview of next lecture

Review: Octahedral Oh ⊃ O group operator structure
Review: Octahedral Oh ⊃ O ⊃ D4 ⊃ C4 subgroup chain correlations
Comparison of O ⊃ D4 ⊃ C4 and O ⊃ D4 ⊃ D2 correlations and level/projector splitting
O ⊃ D4 ⊃ C4 subgroup chain splitting
O ⊃ D4 ⊃ D2 subgroup chain splitting (nOrmal D2 vs. unOrmal D2)
Oh ⊃ O ⊃ D4 ⊃ C4 and Oh ⊃ O ⊃ D4 ⊃ C4v ⊃ C2v subgroup splitting
Splitting O class projectors Pμ into irreducible projectors Pμm4m4 for O ⊃ C4
Development of irreducible projectors Pμm4m4 and representations Dμm4m4
Calculating PE0404 , PE2424, PT10404, PT11414, PT22424, PT21414
O ⊃ C4 induced representation 04(C4)↑O ~ A1 ⊕ T1 ⊕ E and spectral analysis examples
Elementary induced representation 04(C4)↑O
Projection reduction of induced representation 04(C4)↑O
Introduction to ortho-complete eigenvalue-parameter relations
Examples in SF6 spectroscopy

Review Idempotent projector splits Pμm,m of O⊃C4 PE0404 PE2424 PT11414 PT22424 PT21414
Review Coset factored splitting of projectors for O⊃D4⊃C4 into split classes and level structure
Hamiltonian level cluster models with subgroup-defined tunneling parameters
Diagonal idempotent Pμm,m parameter sets for O⊃C4 and O⊃C3 case of SF6 level clusters
Off-diagonal nilpotent Pμm,n (m≠n) parameter sets needed for O⊃C2 clusters
Deriving nilpotent projectors Pμm,n and ireps Dμm,n by fundamental g!Pμm,n relations:
(a) Pμm,m gPμn,n=Dμm,n(g)Pμm,n (b) g=ΣμΣm,nDμm,n(g)Pμm,n (c) Pμn,n=(lμ/°G)ΣgDμ*m,n(g)g
Review of nilpotent projectors for simple D3⊃C2 ~ C3v⊃Cv chains
Calculating and Factoring PT11404 and PT11434
Structure and applications of coset tabulated Dμm,n irreps for various Oh subgroup chains
Oh⊃D4h⊃C4v , Oh⊃D3h⊃C3v , Oh⊃C2v
Comparing Oh ⊃ D4h ⊃ D2h and Oh ⊃ D3d ⊃ C2 representations (T1 vector-type)
Examples of off-diagonal tunneling coefficients DE0424
Comparing Local C4, C3, and C2 symmetric spectra of Oh-symmetric tensors >T[4]+T[6]
Monster clusters: When local C2 symmetry dominates
Comparing off-diagonal O ⊃ C2 parameter sets to CH4 models with cluster-crossings

Spin-spin (1/2)2 product states: Hydrogen hyperfine structure
Kronecker product states and operators
Spin-spin interaction reduces symmetry U(2)proton×U(2)electron to U(2)e+p
Elementary 1⁄2 × 1⁄2 Clebsch-Gordan coefficients
Hydrogen hyperfine levels: Fermi-contact interaction, Racah’s trick for energy eigenvalues
B-field gives avoided crossing
Higher-J product states: (J=1)⊗(J=1)=2⊕1⊕0 case
Effect of Pauli-Fermi-Dirac symmetry
General U(2) Clebsch-Gordan-Wigner-3j coupling coefficient formula
LS to jj Level corralations
Angular momentum uncertainty cones related to 3j coefficients
Multi-spin (1/2)N product states Magic squares
Intro to U(2) Young Tableaus
Intro to U(3) and higher Young Tableaus and Lab-Bod or Particle-State summitry
U(2) and U(3) tensor expansion of H operator
Tensor operators for spin-1/2 states: Outer products give Hamilton-Pauli-spinors
Tensor operators for spin-1 states: U(3) generalization of Pauli spinors
4th rank tensor example with exact splitting of d-orbital

Substitution Group products: Sn cycle notation
Cyclic product algebra: bicycles, tricycles, quadricycles
Permutation unraveling
Product arrays - shortcuts
Sn class transformation algebra
Sn class cycle labeling
Sn class cycle counting
Sn tableaus spin-symmetry and characters: Xn and XYn molecules
Tableau dimension formulae
Methane-like XY4 Introducing rovibrational spectral nomogram
Large molecule character and correlation formulae
Hexa-flouride-like:XY6.
How does level clustering affect nuclear hyperfine?

U(2) tensor product states and Sn permutation symmetry
Rank-1 tensor (or spinor)
Rank-2 tensor (2 particles each with U(2) state space)
2-particle U(2) transform and permutation operation
S2 symmetry of U(2): Trust but verify
Applying S2 projection to build DTran
Applying DTran for S2
Applying DTran for U(2)
S3 permutations related to C3v~D3 geometry
S3 permutation matrices
Hooklength formula for Sn reps
S3 symmetry of U(2): Applying S3 projection (Note Pauli-exclusion principle basis)
Building S3 DTran T from projectors
Effect of S3 DTran T: Introducing intertwining S3 - U(2) irep matrices
Multi-spin (1/2)N product state (Comparison to previous cases)

Generic U(3)⊃R(3) transformations: p-triplet in U(3) shell model
Rank-1 vector in R(3) or “quark”-triplet in U(3)
Rank-2 tensor (2 particles each with U(3) state space)
U(3) tensor product states and Sn permutation symmetry
2-particle U(3) transform. 2-particle permutation operations
S2 symmetry of U(3): Applying S2 projection
Matrix representation of Diagonalizing Transform (DTran T)
Effect of S2 DTran T on intertwining S2 - U(3) irep matrices
S3 symmetry of U(3): Applying S3 projection
Applying S3 character theory
Frequency formula for D[μ] with tensor trace values
Effect of S3 DTran T on intertwining S3 - U(3) irep matrices
Structure of U(3) irep bases
Fundamental “quark” irep. “anti-quark”. “di-quark”.
The octet “eightfold way” The decapalet and Ω-
The p-shell in U(3) tableau plots
Hooklength formulas
Single particle p1-orbitals: U(3) triplet
Elementary U(N) commutation
Elementary state definitions by Boson operators
Summary of multi particle commutation relations
Symmetric p2-orbitals: U(3) sextet
Sample matrix elements
Combining elementary “1-jump” E12, E23, to get “2-jump” operator E13
Review: Representation of Diagonalizing Transform (DTran T)
Relating elementary Ejk matrices to Tensor operator Vkq (ℓ=1 atomic p-shell)
Condensed form tensor tables for orbital shells p: ℓ=1, d: ℓ=2, f: ℓ=3, g: ℓ=4.
Tableau calculation of 3-electron ℓ=1 orbital p3-states and Vkq matrices
Tableau “Jawbone” formula
Calculate 2n-pole moments
Comparison calculation of p3-Vkq vs. calculation by cfp (fractional parentage)
Complete set of Ejk matrix elements for the doublet (spin-1⁄2) p3 orbits
Level diagrams for pure atomic shells p n=1-6, d n=1-5, f n=1-7
Classical Lie Groups used to label f-shell structure (a rough sketch)

Complete set of Ejk matrix elements for the doublet (spin-1⁄2) p3 orbits
Detailed sample applications of “Jawbone” formulae
Number operators
1-jump Ei-1,i operators
2-jump Ei-2,i operators
Angular momentum operators (for later application)
Multipole expansions and Coulomb (e-e)-electrostatic interaction
Linear multipoles; P1-dipole, P2-quadrupole, P3-octupole,...
Moving off-axis: On-z-axis linear multipole Pℓ(cosθ) wave expansion:
Multipole Addition Theorem (should be called Group Multiplication Theorem)
Coulomb (e-e)-electrostatic interaction and its Hamiltonian Matrix elements
2-particle elementary ejk operator expressions for (e-e)-interaction matrix
Tensor tables are (2ℓ+1)-by-(2ℓ+1) arrays (pkq) giving Vkq in terms of Ep,q.
Relating Vkq to Em′,m by (pkq) arrays
Atomic p-shell ee-interaction in elementary operator form
[2,1] tableau basis (from p.29) and matrices of v1 dipole and v1•v1=L•L
[2,1] tableau basis (from p.29) and matrices of v2 and v2•v2 quadrupole
4S,2P, and 2D energy calculation of quartet and doublet (spin-1⁄2) p3 orbits
Corrected level diagrams Nitrogen p3

Marrying spin s=1⁄2 and orbital ℓ=1 together: U(3)×U(2)
The ℓ=1 p=shell in a nutshell
U(6)⊃U(3)×U(2) approach: Coupling spin-orbit (s=1⁄2, ℓ=1) tableaus
Introducing atomic spin-orbit state assembly formula
Slater determinants
p-shell Spin-orbit calculations (not finished)
Clebsch Gordan coefficients. (Rev. Mod. Phys. annual gift)
Sn projection for atomic spin and orbit states
Review of Mach-Mock (particle-state) principle
Tableau P-operators on orbits
Tableau P-operators on spin
Fermi-Dirac-Pauli anti-symmetric p3-states
Boson operators and symmetric p2-states
Connecting to angular momentum
Projecting to angular momentum

[2,1] tableau states lowered by L-=√2(E21+E32)
Top-(J,M) states thru mid-level states
ℓ=1 p=shell LS states combined to states of definite J
J=3/2 at L=0 (4S). J=5/2 at L=2 (2D)
Clebsch-Gordon coupling; J=3/2 at L=2 (2D)
J=3/2 at L=1 (2P)
J=1/2 at L=1 (2P)
Boson operators and symmetric p2-states
The simplest assembly
ℓ=1 p=shell LSJ states transformed to Slater determinants from J=3/2 (4S)
Slater functions for J=5/2 (2D)
(Next class)
Slater functions for J=3/2 (2D)
Slater functions for J=3/2 (2P)
Application to spin-orbit and entanglement break-up scattering

[2,1] tableau states lowered by L-=√2(E21+E32)
Top-(J,M) states thru mid-level states
ℓ=1 p=shell LS states combined to states of definite J
J=3/2 at L=0 (4S), J=5/2 at L=2 (2D)
C-G coupling; J=3/2 at L=2 (2D), J=3/2 at L=1 (l=1 p=shell LSJ states transformed to Slater determinants from J=3/2 (2P), J=1/2 at L=1 (2P)
Spin-orbit state assembly formula and Slater determinants
ℓ=1 p=shell LSJ states transformed to Slater determinants from J=3/2 (4S)
Slater functions for J=5/2, J=3/2 (2D)
Slater functions for J=3/2 (2P), J=1/2 (2P)
Summary of states and level connection paths
Symmetry dimension accounting
Spin-orbit Hamiltonian matrix calculation
Application to spin-orbit and entanglement break-up scattering
SF6 has octahedral (Oh⊃O⊃C4v or C3v) symmetry
SF6 octahedral (Oh⊃C4v) Cartesian coordination
SF6 octahedral (Oh⊃C4v) symmetry coordination
SF6 octahedral (Oh⊃C4v) mode labeling
Ireps for O⊃D4⊃D2 subgroup chain and coset factored projectors
Sorting |T1u〉A, |T1u〉B, and |T1u〉C mode vectors
Combining |T1u〉A, |T1u〉B, and |T1u〉C into two states of zero momentum
Matrices of force F, mass m, and acceleration a for mode dynamics
Acceleration matrix a for 2-by-2 T1u ABC-mode dynamics
Modes and energy level diagrams: SF6, UF6, etc.
SF6, overtones and harmonics
Coriolis orbits of T1u modes ν3 (947cm-1) and ν4 (630cm-1) of SF6
Graphical interpretation of Coriolis T1u effects in ν4 (630cm-1)
Rovibronic Nomogram of Coriolis T1u effects
Tensor centrifugal and Coriolis T1u effects in ν4 P(88) fine structure
Nomogram of T1u SF6 ν4 P(88) fine, superfine, and hyperfine structure

Conservation of rovibronic spin species-Two views: Herzberg vs. 2005
Where SF6 spin species go to die: O⊃C4 and O⊃C3 symmetry breaking
Diatomic or linear molecule symmetry O(3)⊃D∞h
State labels by symmetry O(3)⊃D∞h
Coriolis and λ-doubling levels
Nomograms for dipole-allowed transitions
XYn molecules: S3-S6 tableau-characters
Tableau dimension formulae for X4 and XY4 molecules
CH4 and DH4 (J=7) transitions. SiF4 (J=30) spectra
Possible SiF4 High J superhyperfine levels
Calculating SF6 characters and correlations of symmetry Oh to S6 SF6 levels & spectra
Born-Oppenheimer Approximation (BOA) for RES
Born-Oppenheimer Approximation (BOA)-constricted body wave vs. lab-wave
Weak-coupling “hook-up” vs. stronger “BOA-constricted” wavefunctions
Semiclassical Rotor-“Gyro”-Spin coupling
Semiclassical Rotor-“Gyro”-Spin Rotational Energy Surfaces (ZIPPed)
Rotational energy eigenvalue surfaces (REES) (UnZIPPed)
REES for high-J Coriolis spectra in SF6
*ZIPP (Zero-Interaction-Potential-`Proximation
REES for high-J Coriolis spectra in υ3 CF4x
REES for high-J and high-υ rovibration polyads
Compare tetrahedral/octahedral symmetry Oh⊃Th to Icosahedral Ih⊃Th
Famous (but rare ) molecules with Ih symmetry Buckyballs at the U of Arkansas?
Human rhinovirus 3: Rare in physics (But, all too common in public life)
Ih⊃I Symmetry slide rules (Dodecahedral and Icosahedral versions)
Icosahedral rotation operation classes in subgroup I⊂Ih I-group product table and classes
Icosahedral subgroup I⊂Ih isomorphic to even-permutation group A5⊂S5
C60 Cartesian coordination at Carbon atom vertices
Force vectors and matrices
Ih characters χ(α) and irreps d(A)↑D(α) and D(α)↓d(A)correlations. Icosahedral irreps D(α)
Icosahedral Ih irreps for A-orbits and B-orbits F-matrices projected for diagonalization
C60 Force matrix eigenfrequencies: Infrared-active and Raman-active
Scalar Coriolis effects of IR-active C60 PQR-bands
Varying parameters p=1-h makes frequency clusters D5 modes check C60 modes
Tensor centrifugal effects for high-J rotation of C60 Rotational-Energy-Surfaces (RES)
Bose exclusion in 12C60 vs Fermi proliferation in 13C60
Comparing SF6 with 13C60 and CF4 and OsO4 with 12C60...
Total nuclear spin-weights of each 13C60 symmetry species
13C60 superfine cluster structure prediction Insight by Rotational Energy Surfaces (RES)
13C12C59 isotopomers and their RES
Some history of C60 discoveries