
Legendre contact transformation for
relativistic mechanics
| Page in Textbook | |
|---|---|
| Cover | 4 |
| Introduction | 4 |
| Review and plan of attack: Relativity of pairs | 4 |
| Chapter 1 Continuous Wave (CW) vs. Pulse Wave (PW) functions | 4 |
| Phase velocity for 1-CW | 4 |
| Axioms for light: 2-CW vs. 2-PW | 4 |
| Astronomical view of CW axiom | 4 |
| Spectroscopic view of CW axiom | 4 |
| Time reversal axiom | 4 |
| Phase invariance axioms viewed in a classical way | 4 |
| CW squares vs. PW diamonds in space-time plots | 4 |
| CW wave-zeros vs. PW pulse paths | 4 |
| Comparing wave-like vs particle-like behavior | 4 |
| Wave-zero (WZ) and pulse-peak (PP) space-time coordinate grids | 4 |
| Chapter 2 When Light Waves Collide: Relativity of waves in spacetime | 4 |
| CW-Doppler derivation of relativity | 4 |
| First things first | 4 |
| Lorentz-Einstein transformations | 4 |
| Geometry of Lorentz-Einstein contraction-dilation | 4 |
| Chapter 3. Invariance and Relative Phase: Galileo’s revenge | 4 |
| Geometry of relative phase | 4 |
| Geometry of Doppler factors | 4 |
| Doppler rapidity and Euclid means business | 4 |
| Invariance of proper time (age) and frequency (rate of aging) | 4 |
| Chapter 4. Mechanics based on CW axioms | 4 |
| Quantized cavity modes and “fuzzy” hyperbolas | 4 |
| Alternative definitions of wave mass | 4 |
| Absolute vs. relative phases: Method in madness | 4 |
| Chapter 5. Classical vs. quantum mechanics | 4 |
| Contact transformation geometry of a relativistic Lagrangian | 4 |
| Geometry of circular and hyperbolic functions | 4 |
| Hyper-circular contacts | 4 |
| Transverse vs. longitudinal Doppler: Stellar aberration | 4 |
| Graphical wave 4-vector transformation | 4 |
| Symmetry and conservation principles | 4 |
| 1st and 2nd Quantization: phase vs. amplitude | 4 |
| Chapter 6. Variation and quantization of optical amplitudes | 5 |
| Maxwell amplitudes and energy | 5 |
| Quantized optical fields | 5 |
| Relativistic 1-CW covariance of Poynting flux | 5 |
| Relativistic 2-CW invariance of cavity quanta | 5 |
| N-Photon vs Coherent-?-states | 5 |
| Fuzzy hyperbolas vs. fuzzy coordinates | 5 |
| Deeper symmetry aspects of pair creation | 5 |
| Chapter 7. Compton Effects and Optical Transitions | 5 |
| 1-photon kinematics for emission and absorption of light | 5 |
| The kicker: Recoil shifts | 5 |
| This is not rocket science! (Or is it?) | 5 |
| 2-photon processes: Rayleigh-Thompson-Compton scattering | 5 |
| Car 54 where are you? | 5 |
| Suspended 2-photon diamonds | 5 |
| Feynman’s Father’s query | 5 |
| Photo-absorption and Compton effects | 5 |
| Compton-Doppler staircase | 5 |
| Compton wavelength sum rule | 5 |
| Geometric transition series | 5 |
| Optical PW bounce and accordian-like CW shifts | 5 |
| Chapter 8. Wave Frame Acceleration | 5 |
| Chirping and Einstein elevators | 5 |
| Constant velocity gives constant acceleration | 5 |
| Wave geometry vs. Newton | 5 |
| Pair creation and quantum frames | 5 |
| References | 5 |
| Acknowledgements | 5 |
| -- The Purest Light and a Resonance Hero – Ken Evenson (1932-2002) -- | 5 |
Preceding
Units 1 thru 4 on mechanics and wave resonance are prerequisites to modern
physics of spacetime relativity and quantum
wave mechanics introduced here in
Unit 8. A wave based geometric approach helps to understand special relativity
(SR) and quantum mechanics (QM) while it shows that these two pillars of modern
physics are actually belong to the same subject!
SR
and QM have been treated in separate texts as different and even inimical
subjects. (SR is most often found in E&M texts.) While advanced quantum
field theory treatments do integrate special relativity they do it in a
mathematical way that lacks lucidity and physical intuition. The present
development seeks to improve the situation by appealing to the detailed
geometry of wave interference.
Separated
introductions to SR and QM lead to misconceptions for professional physicists
as well as for their students. In spite of its simple algebra, SR is also
regarded as mysterious. Student comments for SR and QM courses are typically,
“Well, I didn’t understand it, but neither did the prof!” Comments on a QM and SR derivation by an editor of
the Journal of Modern
Optics in 2003 illustrate the problem:
“Even Schroedinger probably never claimed to have a
derivation, and we
certainly don't tell our
students that we
have one. (A) Hand-waving, inspired guess is more like
it.”
A key problem has been a failure to clarify wave mechanics. Consider the editor’s next comment.
“It is quite arbitrary how one defines
envelope and carrier parts of a wave. Usually this is done only when all
frequencies are nearby and all k-vectors are nearby. Then something like the
analytic signal formulation can be used to arrive at unique but still arbitrary
definition.”
This statement exposes a pernicious blind spot in
conventional wave analysis. Its resolution uses Unit 4 expo-cosine
relations in (4.3.30) to clearly separate a wave envelope from its “carrier”
phase.
(4.3.30) repeat a (4.3.30) repeat b
These
are true regardless of how “nearby” are arguments a=(kax-Ěat) or b=(kbx-Ěbt) or their constituent
frequency-time Ěa,bt and wavevector-space ka,bx terms. Identities (4.3.30) separate a wave’s modulus or group envelope embodied by the cosine or sine factor that
defines the outside envelope or “skin” of a wave sketched in the figure below.
The modulus is the factor that remains in the expression Ņ*Ņ for intensity while the phase
part ei(a+b)/2 of Ņ
cancels the e-i(a+b)/2 of Ņ* leaving real intensity |Ņ|2 or MOD |Ņ|.
Envelope
is thus distinguished from a wave’s argument or overall
phase held by exponential factor ei(a+b)/2.
The
latter governs real (Re Ņ) and imaginary (Im Ņ) “carrier”parts that are the inside “guts” of the wave shown in the
sketches below. (One may imagine a boa constrictor that has swallowed live
prey.)
The speed of the wave factor is called group velocity. This external “skin” of the wave is the
only part visible to probability or intensity measurements of Ņ* Ņ.
Meanwhile the speed of exponential phase factor inside the envelope is called mean phase velocity or just plain phase
velocity. Internal phase “guts” may oscillate very rapidly and be
difficult or impossible to measure directly.
Review
and plan of attack: Relativity of pairs
Our
plan of attack in Unit 3 for relativity and quantum theory has similar
philosophy to that of Unit 1 for classical Newtonian mechanics and Unit 4 for
resonance. The idea is to develop the axioms, rules, or laws of physics using relativity of elementary pairs. It is a kind of Occam-razor philosophy.
In
Unit 1 we began with collisions between a pair of cars or a pair of bouncing
super-balls and developed the rules of classical mechanics. In Unit 4 we used a
pair of coupled pendulums to establish the rules of resonant energy transfer.
Here in Unit 8 we use a pair of light waves to find the rules of relativity and
quantum mechanics. Geometry is a key part of this analysis as before.
At
first, the approach seems almost childish in simplicity. Who hasn’t seen (or
been) a child who puts two beetles together to see if they will fight (or
whatever)? Relation between pairs is something that first comes to mind when we
see new things. Unfortunately, human egocentricity steers us toward a more
complicated pair, a single thing and you. That’s the adult analytic approach, isn’t it?
Conventional
“adult” mechanics books begin with axioms for a single mass or “particle” acted
on by “outside forces” (presumably you) to move according to Newton laws 1 thru 3.
Detailed treatment of all these laws at the start is usually not a favorite
pastime for either instructor or student. The algebra or calculus is tedious
and it is difficult at first to arrange neat compelling and demonstrative
experiments.
In
contrast, Unit 1 starts off with just a single axiom (Newton law-1 of momentum
conservation) for particle-pair
mechanics and derives collision kinematics by simple geometry using
velocity-velocity V1-V2 plots. This clearly exposes Galilean relativity
symmetry and the logic of m1V1+m2V2 conservation. An almost child-like geometric
simplicity of particle-pair relativity economizes the logic.
Pair
relativity easily finds results for neat first-day experiments by ignoring
(until later) the “you” and your “outside force.” Energy conservation is then
proved using V1-V2 geometry and time symmetry. An autonomous
one-pair-at-a-time mechanics leads later to multi-mass force and potential
relations that also have an Occam-cut-to-the-chase logic that may be derived
using plane geometry.
In
Unit 4, resonance mechanics is based on autonomous pairs of coupled pendulums
described by phasor-pair plots of x1-V1 versus x2-V2 or complex Į1 versus Į2 plots. Again, the key idea is pair-relative.
Energy transfer rate is the product (|Į1||Į1|sin Ė) of
phasor amplitudes and sine of relative phase angle Ė. Autonomous
one-phasor-pair-at-a-time mechanics have a direct cut-to-the-chase geometric
logic that then leads to multi-phasor wave mechanics, Fourier spectral
analysis, and dispersion relations. Very important is a logic for complex pairs
of numbers and for U(2) pairs of complex phasors in the study of resonance.
In
Unit 8, the protagonists are a pair of colliding (counter-propagating) laser
continuous waves (CW). Here we contemplate what happens at the micron level in
the collision region of two bluish green beams of 600 THz dye laser, and arrive at an extraordinary claim.
A pair of CW light beams can show the rules of classical mechanics, quantum
mechanics, and special relativity.
What
a claim! These green beams can expose the fundamental logic of three hard
physics courses CM, QM, and SR all for a fraction of the price one of them.
And, like the late night TV ad, that’s not all! For just a little more you can
get EM (electro-magnetism) thrown into the bargain.
How
can it be possible to conjure rules about mechanics of mass particles from
light waves? A 1939 theory by Dirac and a 1950 experiment by Anderson provide some
advance motivation for such thought-experimentation. What Dirac theorized and
Anderson demonstrated are results of colliding two high-energy light beams.
Crossing two gamma-(č)-ray beams can convert light to matter plus anti-matter in č+č electron-positron pair production reactions. This primal chemistry is denoted as
follows.
![]()
The idea that 0.51MeV č-rays
can produce positronium pairs is taken for granted by many high-energy
physicists, but it should be a mind-boggling Genesis-moment for any thinking
student of physics.

Now
green 600 THz lasers
do not produce positronium matter. The č-frequency mc2/h=0.1ExaHz is about a million times more than our lasers can go. (That’s just as
well given current world politics!) But, any two lasers can produce something that obeys symmetry conditions for matter waves, and it is those symmetry “laws”
and geometry that underlie all our mechanics whether classical, quantum,
relativistic, or electromagnetic. CW laser beams may not be matter but
they do expose some of its kinematics.
Ideal
CW-laser pairs help us derive fundamental relativistic or quantum concepts and
formulas by ruler and compass in just a few steps. A number of concepts,
quantities, and relations are exposed in Unit 3 by wave geometry. These include
longitudinal Doppler shifts, Einstein-Lorentz-Minkowski frames, time dilation,
length contraction, stellar aberration, transverse Doppler effects,
mass-energy-momentum dispersion relations, Legendre-Lagrange-Hamilton-Poincare
relativistic contact transformations, Compton recoil shifts, Compton
scattering, polarization and spin transformation, acceleration by frequency
chirps, Einstein wave-elevators, and quantum count-rate covariance.
According
to a historical footnote given to me by Dudley Herschbach, Einstein became
fascinated with ruler and compass geometry when he was just five years old. We
can only guess the age Euclid was when he first picked up a Babylonian compass.
In any case, a ruler and compass is child’s play, first and foremost, and
therein lies a certain pedagogical power.
We
cannot know if either of these gentlemen would welcome a geometric approach to
relativity and quantum theory. I would like to think so, but it’s possible they
might have taken a Bourbakian view and found all these pictures to be just so
childish. If so then it’s their loss and our gain!
Chapter
1 Continuous Wave (CW) vs. Pulse Wave (PW) functions
The
standard units of time t and space x are seconds and meters. Pure waves are labeled by inverse units that
count waves per-time or frequency
í,
which is per-second or Hertz (1Hz=1 s-1) and waves per-meter that is called wavenumber ź whose
old units were Kaiser (1 K=1 cm-1=100
m-1). Inverting back gives
the period ô=1/í or time for one wave and wavelength
Ď=1/ź or the space occupied by one wave.
Physicists like angular or radian quantities of radian-per-second or angular frequency Ě=2ðí and radian-per-meter or wavevector k=2ðź in
plane continuous wave (CW) functions Ņ.
![]() . (1.1a)
. (1.1a)
Sine
or cosine are circular functions of wave phase (kx-Ě t) given in radians and defined here.
![]() (1.1b)
(1.1b)
![]() (1.1c)
(1.1c)
They
relate time ô and space Ď parameters to
per-time Ě or í and per-space k or ź wave parameters.
Spacetime
plots of the real field ![]() for one CW laser light are shown in Fig. 1.1. The
left-to-right moving wave
for one CW laser light are shown in Fig. 1.1. The
left-to-right moving wave ![]() in Fig. 1.1(a) has a positive wavevector k while k is negative
for right-to-left moving wave
in Fig. 1.1(a) has a positive wavevector k while k is negative
for right-to-left moving wave ![]() in Fig. 1.1(b). Light and dark lines mark time
paths of crests, zeros, and troughs of
in Fig. 1.1(b). Light and dark lines mark time
paths of crests, zeros, and troughs of ![]() . A zero-phase line (where kx-Ě t is zero) or crest line has slope c=Vphase.
. A zero-phase line (where kx-Ě t is zero) or crest line has slope c=Vphase.
![]() (1.1d)
(1.1d)
Each
white line in Fig. 1.1 has a phase is an odd multiple (N=1,3,…) of Ļ/2 and marks a
Ď/2-interval.
![]()
Slope
or phase velocity Vphase of all lightwave phase line is a universal constant c=299,792,548m/s.
(Note tribute to Ken Evenson’s c-measurement in Unit 4.) Velocity is a ratio of
space to time (x/t) or a ratio of per-time to per-space (í/ź) or (Ě /k), or a product of per-time and space (íĎ)=1/(ôź).
The
standard wave quantities of (1.1) are labeled for a long wavelength example
(infrared light) in the lower part of Fig. 1.1. Note that the ![]() wave precedes the
wave precedes the ![]() wave. A simple mnemonic is helpful, “Imagination precedes reality by one quarter.” and applies to combined waves, too.
wave. A simple mnemonic is helpful, “Imagination precedes reality by one quarter.” and applies to combined waves, too.
Axioms for light: 2-CW vs. 2-PW
Beginning
relativity courses paraphrase Einstein’s light speed axiom as in Fig. 1.2a, “Speed of a
lightning flash is c according to passengers of any train,” or
simply, “Pulse wave
(PW) speed c is invariant.”
For critically thinking students, that is a show-stopper. It boggles the mind
that something of finite speed cannot ever be caught up to, indeed, cannot even begin to be caught.[i]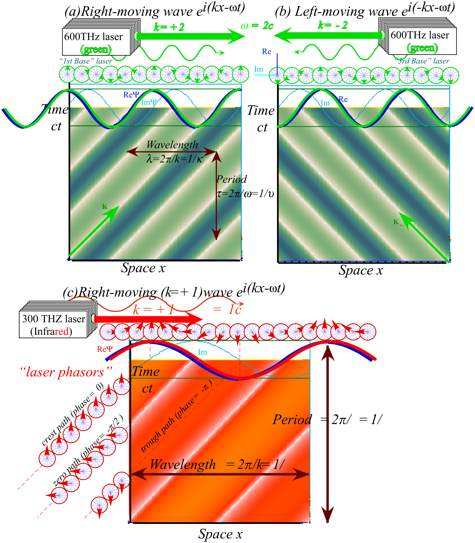
Fig. 1.1 Phasor
and spacetime plots of moving CW laser waves. (a) Left-to-right. (b)
Right-to-left.
Occam’s
razor can dissect the c-axiom
into a less mind-boggling form. As Evenson viewed a frequency chain of multiple
“colors” of continuous wave (CW) laser beams, he assumed that, “All colors have speed c.”
Had Einstein imagined trains viewing a 600THz (green)
laser as in Fig. 1.2b, his c-axiom
might be, “CW speed is c
according to passengers of any train while frequency and wavelength vary by
a Doppler effect that depends on velocity of the train,” or more simply, “All
colors go c.”
A
CW spectral component of a PW has a color variation with observer speed that a
“white” PW does not. A colored wave (CW) will blue-shift if you approach its
source or a red-shift if you run away from it. Doppler’s theory of acoustical
wave frequency shift existed 200 years before radar, masers, and lasers showed
the ultra-precise 1st-order Doppler sensitivity of a coherent
optical CW.
Also
an optical Doppler shift depends on one relative velocity of source and observer while acoustical
Doppler depends on three absolute (or three relative) velocities involving source,
observer, and a “wind.” This
single-velocity simplicity of en vacuo optical Doppler shifts is crucial for relativity.
Consider a 600THz green wave from a 600THz source. One may ask, “Is it distinguishable from another 600THz green wave sent by a 599THz source approaching or a 601THz source departing at just the right speed? Or, could 600THz light, seen as we approach a fixed 599THz source, ever differ in speed from 600THz light seen as we depart a fixed 601THz source? How many kinds of 600THz light exist?”
Evenson’s
axiom follows if one answers, “There is only one kind of each frequency (color)
and only one speed independent of source or observer velocity.” An undesirable
alternative is to have many different kinds of each color, corresponding to
many ways to make each color by tuning source up (or down) while moving out (or
in). (In fact, one color illuminating a gas, liquid, or solid may involve two
or many varieties of mode dispersion with wave speeds ranging above or below c.) Evenson’s axiom demands that light in
a vacuum be one speed for all frequency. In short, light is dispersion-free.
If
so, a PW must move rigidly at the speed c
shared by its component CW colors. In this way one derives Einstein’s PW law as
a theorem
arising from Evenson’s CW axiom. Occam wins one!
It
also relates to appearance of distant nebulae and the night sky. If any colors
were even a fraction of a percent slower than other frequencies, they would
show up thousands or millions of years later with less evolved images than
neighboring colors. We might then enjoy a sky full of blurry colorful streaks
but would lose the clarity of Hubble astronomical images of colliding galaxies
billions of light years away.
Spectroscopic view of CW axiom
Astronomy
is just one dependent of Evenson’s CW axiom. Spectroscopy is another. Laser
atomic spectra are listed by frequency õ (s-1) or period ô=1/õ
(s) while early tables list atomic lines from gratings by wavenumber ź
(m-1) or wavelength Ď=1/ź (m). The equivalence of time and space
listings is a tacit
assumption in
Evenson’s axiom. The axiom may be stated by the following summary of (1.1a-d).
c = õ ŠĎ
= Ď/ô = õ/ź = 1/(ź Šô)
= c =299,792,548m/s (1.1)summary
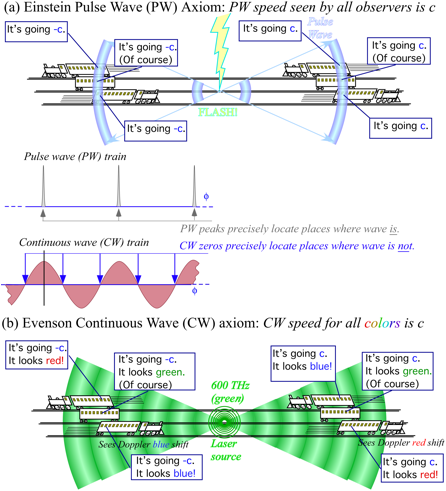
Fig.
1.2 Comparison of wave archetypes and axioms. (a) Pulse Wave (PW) peaks locate where
a wave is. Their speed is c for all observers. (b) Continuous Wave (CW)
zeros locate where it is not. Their speed is c for all colors (or
observers.)
An
atomic resonance is temporal and demands a precise frequency. Sub-nanometer atomic radii are thousands of times smaller
than micron-sized wavelengths of optical transitions. Optical wavelength is not
a key variable in atomic dipole approximations that ignore spatial dependence
of light.
However,
optical grating diffraction demands precise spatial fit of micron-sized wavelength to micron grating slits. Optical
frequency is not a key variable for time independent Bragg or Fraunhofer laws.
Spatial geometry of a spectrometer grating, cavity, or lattice directly
measures wavelength Ď, and then frequency õ is determined indirectly from Ď
by axiom (1.1). That is valid if the light speed c = õ ŠĎ is invariant throughout the spectrum
(and throughout the universe.)
A
spectroscopist expects an atomic laser cavity resonating at a certain atomic
spectral line in one rest frame to do so in all rest frames. Each Ď
or õ value is a proper
quantity to be stamped on
the device and officially tabulated for its atoms. Passersby may see output õ Doppler red shifted to rõ or blue shifted to bõ.
Nevertheless, all can agree that the device and its atoms are actually lit up
and working!
Moreover,
Evenson’s CW axiom demands that õ and Ď must Doppler shift
inversely
one to the other so that the product õ ŠĎ is always a constant c=299,792,458
mŠs-1. The same
applies to ô and ź for which ź
Šô=1/c. Also, there is an inverse relation that exists between
Doppler blue and red shifts seen before and after passing a source. This is our
second CW axiom. It involves time reversal symmetry.
Atoms
behave like tiny radio transmitters, or just as well, like receivers. Unlike
macroscopic radios, atoms are time-reversible in detail since they have no
resistors or similarly irreversible parts. Suppose an atom A broadcasting frequency õA resonates an approaching atom B tuned to receive a blue shifted
frequency õB = bõA. If time runs backwards all velocity
values change sign. Atom B
becomes a transmitter
of its tuned frequency õB = bõA that is departing from atom A who is a receiver tuned to its frequency õA = (1/b)õB. Atom A
sees õA red-shifted from B’s
frequency õB by an inverse factor r=1/b.
b=1/r (1.2)
Phase invariance axioms viewed in a classical way
Optical
CW axioms may be based on deeper phase invariance principles. Elementary CW
function Į=A
exp i(kŠx-ĚŠt) or its real part Re Į=A cos(kŠx-ĚŠt) has a phase angle Ö=(kŠx-ĚŠt) that is regarded as an invariant or proper quantity. Our
rationale is that each space-time point of the wave has a phase clock or phasor (Re
Į, Im Į)
turning at angular
frequency Ě=2ðŠõ.
Each phasor reading Ö could be stamped or “officially”
tabulated. All observers should agree on Ö even if Doppler shifts change frequency Ě=2ðŠõ and wavevector k
= 2ðź to new values (Ě′,k′) or if space x and time t also transform to x′,t′.
kŠx-Ě Št = Ö = k′Šx′-Ě′Št′ (1.3)
(Lorentz-Einstein
transformations for both space-time x,t
to x′,t′ and inverse space-time (Ě,k) to (Ě′,k′)
are derived in Ch. 2 using CW axioms (1.1) and (1.2) in a few algebraic or
ruler-and-compass steps.)
Historically,
invariance (1.3) relates to classical Legendre contact transforms of Lagrangian
L to
energy E or
Hamiltonian H.
Differential Ldt is
Poincare’s action invariant dS or phase dÖ with an h factor.
![]() (1.4a)
(1.4a) ![]() (1.4b)
(1.4b)
Connecting (1.3)
to (1.4b) requires quantum scaling relations p=hk
of DeBroglie and E=hĚ
of Planck. Ch. 3 shows how such relations arise from CW axioms (1.1-2). Exact
relativistic quantum and classical mechanical relations are found in a few
algebraic[ii]
or ruler-and-compass steps. Elegant wave-geometric[iii]
interpretations of momentum, mass, energy, and Poincare’s invariant are exposed
in Ch. 4 and Ch. 5.[iv]
We
surmised that Einstein might have liked geometric derivations since a compass
first caught his theoretical attention at an age of five.[v]
Perhaps, it might also appeal to Poincare who also discovered relativity around
the time of Einstein’s 1905 annus mirabilis. Poincare phase invariance (1.3)
underlies both CW lightspeed axiom (1.1) and time reversal axiom (1.2).
Consider the Ö=0
point.
kŠx-Ě Št
= 0 (1.5a)
Solving gives
phase velocity x/t (meters-per-second)
equal by (1.1) to õ/ź (per second)-per-(per meter).
![]() (1.5b)
(1.5b)
Doppler shift ![]() leaves phase velocity invariant. Phase Ö=(kŠx-ĚŠt)
itself is invariant to time reversal (
leaves phase velocity invariant. Phase Ö=(kŠx-ĚŠt)
itself is invariant to time reversal (![]() and
and ![]() ) and that supports (1.2), the inverse-Doppler
relation b=1/r.
) and that supports (1.2), the inverse-Doppler
relation b=1/r.
We
find relativistic and quantum derivations based on classical mechanical laws to
be clumsy at best and wrong-way-to at worst. Simple wave interference with
axioms (1.1-2) can unite relativity and quantum theory. At the wave-phasor or
“gauge” level, Nature may be seen as a big wave trick!
Comparing pulsed and continuous wave
trains
It
is instructive to contrast two opposite wave archetypes, the Pulse
Wave (PW) train sketched in
Fig. 1.2a and the Continuous Wave (CW) train sketched in Fig. 1.2b. A CW
is the more elementary theoretical entity, indeed the most elementary entity in classical optics
since it has just one value of angular frequency Ě=2ðŠõ, one value of
wavevector k = 2ðź, and one amplitude A.
![]() (1.6)
(1.6)
The real part is
the cosine wave![]() shown in Fig. 1.2(b). Acronym CW fits cosine
wave, as well. If frequency õ is in the visible 400-750THz
range, then CW could also stand for colored wave.
shown in Fig. 1.2(b). Acronym CW fits cosine
wave, as well. If frequency õ is in the visible 400-750THz
range, then CW could also stand for colored wave.
In
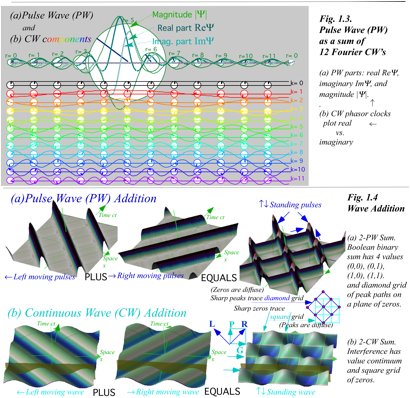
contrast, the PW is a less elementary wave function and contains N harmonic terms of CW functions where
bandwidth N is as
large as possible. Fig. 1.3 shows an example with N=12.
![]() (1.7)
(1.7)
An infinite-N PW is a train of Dirac ä(x-a)-functions each separated by fundamental
wavelength Ď=2ð/k.
The ä
-spikes march in lockstep at light speed c=Ě/k because of Evenson’s CW axiom (1.1).
![]()
Delta functions
have infinite frequency bandwidth and are thus impractical. Realistic PW trains
apply cutoff or tapering amplitudes an to the harmonic so as to restrict
frequency to a finite bandwidth Ä.
![]() (1.8)
(1.8)
One choice is
the Gaussian taper ![]() that gives Gaussian PW functions
that gives Gaussian PW functions ![]() .
.
PW
functions (1.8) involve an unlimited number of amplitude parameters
an in addition to
fundamental frequency Ě, while a CW function has a single
amplitude parameter A.
Thus, theory based on CW properties is closer to an Occam ideal for axiomatic
simplicity than one based on PW.
CW squares vs. PW diamonds in space-time plots
However,
with regard to counter-propagating or colliding beams the PW appear in Fig. 1.4a to have simpler properties
than CW in Fig. 1.4b. PW have a simple classical Boolean OFF (0) over most of
space-time with an occasional ON (1) at a sharp pulse. On the other hand CW
range gradually between +1 and –1 over most of space-time, but have sharp
zeros (0) in between crest and trough. (A PW is designed to make precise peaks that show where it
is. A CW naturally has precise zeros that show where it is not.)
Interference
between two colliding CW makes a square (P, G)-zero-grid that is subtler and sharper
than the left-right moving (L,R)-peak-diamond grid made by two colliding PW.
One should understand how this wave interference works to make these two
archetypical types of wave space-time geometry.
Interference
of colliding PW in Fig. 1.4a or Fig. 1.5b is wysiwye (What you see is what you expect.). The pattern of interference for the sum
of colliding CW in Fig. 1.4b and Fig. 1.5a is subtler. PW paths in space-time (x,ct) resemble baseline diamonds in Fig. 1.5b like paths in the American
baseball sport. Meanwhile, CW zeros form Cartesian space-time
squares in Fig. 1.5a with horizontal
x-axial
fixed time-lines (ct=…1,2…) and vertical temporal ct-axial lines of fixed location (x=…1,2…).
PW
peak diamonds seem simple but hide intricate networks of zeros near each peak.
CW squares make truly simple and precise lattices of standing wave zeros of
given by (1.9), which is just a factored sum of two equal-but-opposite
colliding CW. Note that the group envelope factor![]() is zero on lines (kx/ð+1/2=…0,1,2…) parallel to the ct-axis. The phase factor
is zero on lines (kx/ð+1/2=…0,1,2…) parallel to the ct-axis. The phase factor ![]() has a zero real part on lines of simultaneous time
(ct/ð+1/2=…0,1,2…)
parallel to the x-axis. (At lattice corners, both factors are zero.)
has a zero real part on lines of simultaneous time
(ct/ð+1/2=…0,1,2…)
parallel to the x-axis. (At lattice corners, both factors are zero.)
![]() (1.9)
(1.9)
CW wave-zeros vs. PW pulse paths
Phase
and group wave zeros of 2-CW interference define a space-time wave-zero (P,G)-coordinate
grid for light waves in Fig. 1.5 and more general waves in Fig. 1.6. Vector P points along a phase zero path
and vector G points
along a group zero path. They complement PW pulse peak or peak-path (L,R)-grid
based on vector L that points
along a left moving peak path and a vector R that points along a right moving peak path.
The half-sum-and-difference relation of (P,G)
to (L,R)
is as follows.
P =![]() (L + R) (1.10a)
(L + R) (1.10a)
G =![]() (L - R) (1.10b)
(L - R) (1.10b)
The peak-path
vectors {L,R) are
then given by sum-and-difference of wave zero vectors {P,G).
L = (P + G) (1.10c)
R = (P − G) (1.10d)
Sum-and-differences
are due to phase sum-and-differences. (Recall discussion of (4.8.21) in Unit
4.)
Comparing wave-like vs particle-like behavior
Relations
(1.10) highlight wave-particle duality. First, Newton saw light as
particle-like. Then Young and Maxwell showed its wave-like nature. Finally,
Planck, Einstein, and Compton found particle-like behavior of “photon” quanta.
The label “photon” is reserved for quantum field eigenstates having decidedly
more complicated behavior than is shown in semi-classical wave plots in Fig.
1.6 or colliding light waves in Fig. 1.5. Still the diamond left-and-right
moving PW (L,R)-peak paths in Fig. 1.5b might be thought
of as paths of fictitious particles or “photon bunches” that are well localized
in space-time as they move at Īc
in either direction. Each PW laser “spits” pulses (patooey! patooey!…) at 600Thz.
Optical pulse peaks do move like particles in between the points where “collisions” occur (with very complicated wave interference). After that the “particles” seem to pass through each other or recoil elastically. Newton wrote about optical interference behavior as crazy “light having fits.”
Square 2-CW (P,G) zero-paths in Fig. 1.5a are due to counter-propagating 600Thz CW waves interfering wherever they exist in space-time. The wave between the zeros is delocalized in space-time compared to the PW peaks but the square white zero-lines are extremely sharp as are vectors L=( ck, Ě) and R=(-ck, Ě) that determine motion of left and right CW component laser beams while vectors P=(0,Ě) and G=(Ě,0) determine the real wave-zero lattice of their 2-CW interfering sum.
It
is important to note that these vectors, appropriately scaled, describe both
time-vs-space (x,t)-plots and Fourier inverse per-time-space or reciprocal space-time plots of frequency-vs-wavevector (Ě,k). A
general example of this is derived and shown in a following Fig. 1.6 where the
two kinds of plots may be superimposed. We will see that a (Ě,ck)![]() (ck,Ě) switch
or else an (x,ct)
(ck,Ě) switch
or else an (x,ct)![]() (ct,x) switch to the Newtonian format is needed
in order to make a CW lattice and reciprocal PW lattice coincide and that
entails a (P,G)
(ct,x) switch to the Newtonian format is needed
in order to make a CW lattice and reciprocal PW lattice coincide and that
entails a (P,G)![]() (P,G) switch. This is indicated in Fig. 1.5a to the
right of the square space-time lattice.
(P,G) switch. This is indicated in Fig. 1.5a to the
right of the square space-time lattice.
PW
(L,R)-peak paths are “particle-like” and stand
out in space-time for N-CW wave
trains. Then interference “fits” between pulses die off (to make Newton
comfortable again.) But, CW (P,G)-zero paths, in contrast, are “wave-like”
with very sharp lines in space-time for maximally interfering 2-CW beats.
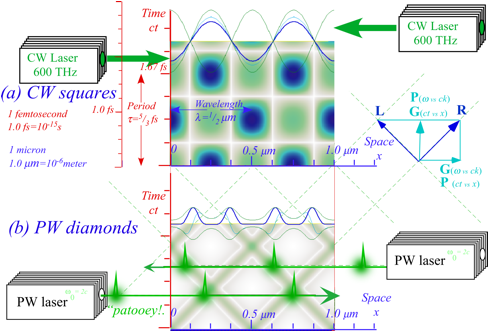
Fig. 1.5 Space-time grids (a) 2-CW standing-wave-zero squares. (b) 2-PW diamond pulse peak paths.
Wave-zero (WZ) and pulse-peak (PP) space-time coordinate grids
The
following Fig. 1.6 and Fig. 1.7 compare and superimpose time-vs-space (x,t)-plots of group and phase waves, on one
hand, with their inverse per-time-space or reciprocal space-time plots of frequency-vs-wavevector (Ě,k), on
the other, and thereby mesh (x,t)-plots with their Fourier transforms.
The
plots apply to all waves and not just to light. The example in Fig. 1.6 begins
by picking four random numbers, say, 1,2,4,
and 4 to
insert into frequency-wavevector K2=
(Ě2,k2)=(1,2) of a mythical source-2 and frequency-wavevector K4=
(Ě4,k4)=(4,4) of another mythical source-4. Velocity c2=Ě2 /k2
=1/2 of source-2 and c4=Ě4 /k4
=1 of source-4 are unequal. For light waves in Fig.
1.7, c2
equals c4
as required by an important axiom discussed in the following Chapter 2.
Let
the continuous waves (CW) from the two sources interfere in a 2-CW sum.
![]() (1.11a)
(1.11a)
To solve for
zeros of this sum we first factor it into a phase-wave eip and a group-wave cos g factor.
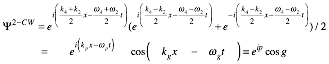 (1.11b))
(1.11b))
Phase factor eip uses the half-sum (Ě,k)-vector Kphase=(K4+K2)/2 in its argument![]() . Group factor cos g has the
half-difference (Ě,k)-vector Kgroup=(K4−K2)/2 in its
argument
. Group factor cos g has the
half-difference (Ě,k)-vector Kgroup=(K4−K2)/2 in its
argument![]() .
.
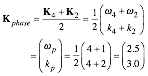 (1.11c)
(1.11c) 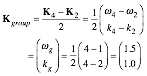 (1.11d)
(1.11d)
The (Ě,k)-vectors Kn define paths and coordinate lattices for
pulse peaks and wave zeros in Fig. 1.6a.
Real zeros (ReĮ=0)
have velocity Vphase on Kphase
paths. Group zeros (|Į|=0) move at Vgroup on Kgroup.
![]() (1.12a)
(1.12a) ![]() (1.12b)
(1.12b)
Zeros of phase factor
real part ![]() lie on phase-zero paths where angle p is N(odd)Šð/2.
lie on phase-zero paths where angle p is N(odd)Šð/2.
![]() .
.
Zeros of group amp-factor![]() lie on group-zero or nodal paths where angle g is N(odd)Šð/2.
lie on group-zero or nodal paths where angle g is N(odd)Šð/2.
![]() .
.
Both factors are zero at wave zero (WZ) lattice points (x,t). This defines the lattice vectors in Fig. 1.6a.
![]() (1.13a)
(1.13a)
Solving
gives spacetime (x,t) zero-path lattice that are white lines in Fig. 1.6a. Each lattice
intersection point is an odd-integer![]() combination of wave-vectors
combination of wave-vectors ![]() and
and ![]() .
.
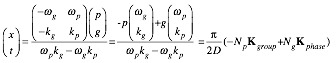 (1.13b)
(1.13b)
So space-time lattice points reuse the base lattice
vectors Kgroup and Kphase of reciprocal per-space-time!Scaling factor 2D/ð =![]() /ð converts
(per-time, per-space)
vectors Kgroup or Kphase into (space, time) vectors
/ð converts
(per-time, per-space)
vectors Kgroup or Kphase into (space, time) vectors ![]() or
or ![]() . (Plot units are set so 2D/ð =1 or D=ð/2. This
works only if D is non-zero.)
. (Plot units are set so 2D/ð =1 or D=ð/2. This
works only if D is non-zero.)
Fig.
1.6b is a lattice of source vectors K2 and K4 (the difference and sum of Kgroup and Kphase).
![]() (1.14a)
(1.14a) ![]() (1.14b)
(1.14b)
Source-2 has
phase speed c2 on K2 paths of slope c2. Source-4 has speed c4 on K4 paths of slope c4.
![]() (1.15a)
(1.15a) ![]() (1.15b)
(1.15b)
One
may view the K2 and K4 paths from a classical or semi-classical viewpoint if pulse
waves (PW) were wave packets (WP) that mimic particles. Newton took a hard-line
view of nature and ascribed reality to “corpuscles” but viewed waves as
illusory. He misunderstood light if it exhibited interference phenomena and
complained that its particles or “corpuscles” were having “fits.” Newtonian corpuscular views are parodied
here by imagining that frequency ![]() (or
(or![]() ) is the rate at which source-2 (or 4)
emits “corpuscles” of velocity c2
(or c4). Then the wavelengths
) is the rate at which source-2 (or 4)
emits “corpuscles” of velocity c2
(or c4). Then the wavelengths![]() (or
(or![]() ) are just inter-particle spacing of K2 (or K4) lines in Fig. 1.6a. Since wavelength Ď2 (Ď4 )
separates K2 (K4) lattice lines in Fig. 1.6b, one can
imagine them as “corpuscle paths.” The paths are diagonals of the Kgroup(Kphase) wave-zero lattice in time vs space (x,t) of Fig. 1.6a.
) are just inter-particle spacing of K2 (or K4) lines in Fig. 1.6a. Since wavelength Ď2 (Ď4 )
separates K2 (K4) lattice lines in Fig. 1.6b, one can
imagine them as “corpuscle paths.” The paths are diagonals of the Kgroup(Kphase) wave-zero lattice in time vs space (x,t) of Fig. 1.6a.
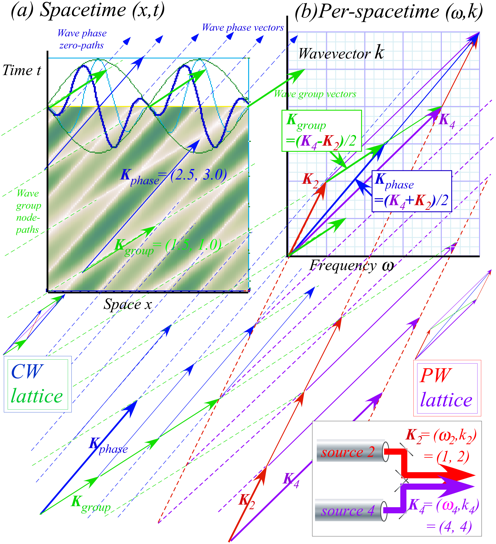
Fig. 1.6 “Mythical” sources and their wave coordinate
lattices in (a) Spacetime and (b) Per-spacetime.
CW lattices of phase-zero and group-node paths intermesh
with PW lattices of pulse, packet, or “particle” paths.
This
development shows wave-particle, wave-pulse, and CW-PW duality in the cells of each CW-PW
wave lattice. Each (K2 ,K4)-cell of a PW lattice has a CW vector 2P or 2G
on each diagonal, and each (P,G)-cell of the CW lattice has a PW vector K2 or K4 on each diagonal. This is due to sum and difference
relations (1.11d) or (1.14b) between (P,G)=(Kphase, Kgroup) and (K2, K4).
In
order that space-time (x,t)-plots
can be superimposed on frequency-wavevector (Ě,k)-plots or (õ,ź)-plots,
it is necessary to switch axes for one of them. The space-time t(x)-plots in Fig. 1.6a follow the convention
adopted by most relativity literature for a vertical time ordinate (t-axis) and horizontal space abscissa (x-axis) that is quite the opposite of Newtonian
calculus texts that plot x(t)
horizontally. However, the frequency-wavevector k(Ě)-plots in Fig. 1.6b switch axes from the
usual Ě(k) convention so that t(x) slope due to space-time velocity x/t or Äx/Ät (meter/second) in Fig. 1.6a matches that of equal
per-time-per-space wave velocity Ě/k or ÄĚ/Äk (per-second/per-meter) in Fig. 1.6b.
Superimposing
t(x)-plots onto k(Ě)-plots also
requires that the latter be rescaled by the scale factor ð /2D
derived in (1.13b), but rescaling fails if cell-area determinant factor D is zero.
![]() (1.16)
(1.16)
Co-propagating
light beams K2= (Ě2,k2)=(2c,2)
and K4= (Ě4,k4)=(4c,4)
in Fig. 1.7b have D=0 since
all K-vectors including Kphase=(Ěp,kp)=(3c,3)
and Kgroup= (Ěg,kg)=(c,1)
lie on one c-baseline
of speed c that
has unit slope (Ě/ck=1) if we rescale (Ě,k)-plots to (Ě,ck) and (x,t)-plots to (x,ct).
In
summary, co-propagating
light waves absolutely fail to make coordinate grids! However, counter-propagating (right-left) light waves are another
“matter” altogether.
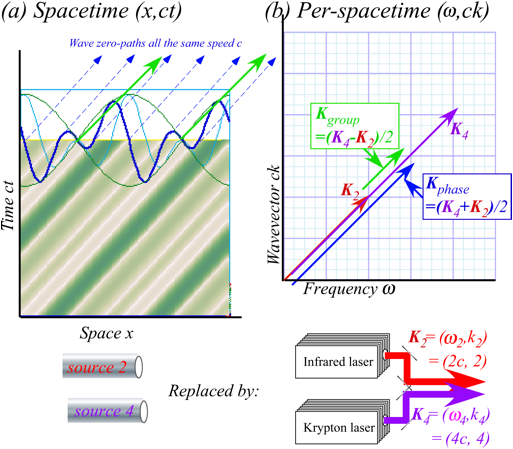
Fig. 1.7 Co-propagating laser beams produce a collapsed wave
lattice since all parts have same speed c.
In
Ch. 2 counter-propagating
(right-left) light wave vectors
(R,L)= (K2,-K4) are used to make CW bases (P= Kphase, G= Kgroup) with a non-zero value for area D =|GxP|. Opposing PW base vectors are sum and
difference (R,L)=(P+G,P-G) of CW
bases so a PW cell area |RxL|
is twice that of CW cell |GxP|.
|RxL|= |(P+G) x (P-G)|=2|GxP| (6.22)
Wave cell areas
due to colliding CW are key geometric invariants for relativity and quantum
mechanics as will be shown. As waves pass us bye and bye, then will
the spray go high and fly.
Chapter
2 When Light Waves Collide: Relativity of waves in spacetime
Let
us represent counter-propagating frequency-Ě laser beams by a baseball diamond in
Fig. 2.1a spanned by CW vectors for waves moving left-to-right (R on 1st base) and right-to-left
(L on 3rd base).
R=K1=(ck1,Ě1)= Ě(1,1) (2.1a) L=K3=(ck3,Ě3)= Ě(-1,1) (2.1b)
Fig. 2.1 uses
conventional (ck,Ě)-plots
for per-space-time and (x,ct)-plots for space-time. Both beams have frequency õ=Ě/2ð=600THz(green),
the unit scale for Ě and ck axes.
For the L-beam, ck equals -Ě.
Phase
vector P=Kphase and group vector G=Kgroup are also plotted in (Ě,ck)-space
in Fig. 2.1b.
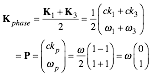 (2.2a)
(2.2a) 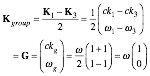 (2.2b)
(2.2b)
Phase and group
velocities of counter-propagating light waves may vary from c. These surely do!
![]() (2.3a)
(2.3a) ![]() (2.3b)
(2.3b)
The extreme speeds
account for the square (Cartesian) wave-zero (WZ) coordinates plotted in Fig.
2.1c. As noted for Fig. 1.5, the group zeros or wave nodes are stationary and
parallel to the time ct-axes,
while the real-zeros of the phase wave are parallel to the space x-axes. The latter instantly appear and
disappear periodically with infinite speed (2.3a) while standing wave nodes
have zero speed (2.3b).
Fig.
2.1d shows 2-way pulse wave (2-PW) trains for comparison with the 2-CW WZ grid
in Fig. 2.1c. As noted for Fig. 1.3, a PW function is an N-CW combination that suppresses its
amplitude through destructive interference between pulse peaks that
owe their enhancement to constructive interference.
Colliding
PW’s show no mutual interference in destroyed regions. Generally one PW is
alone on its diamond path going +c
parallel to 1st baseline R=K1 or going –c parallel to 3rd baseline L=K3.
![]() (2.4a)
(2.4a) ![]() (2.4b)
(2.4b)
But
wherever two PW peaks collide, each of the CW pairs will be seen trying to form
a square coordinate grid that 2-CW zeros would make by themselves. This begins
to explain the tiny square “bases” seen at the corners of the space-time
“baseball diamonds” in Fig. 2.1d simulation.
CW-Doppler derivation of relativity
Evenson’s
CW razor-cut of Einstein’s PW axiom improves relativity development. However,
quantifying Einstein’s popular (and still common) derivation is difficult as is
a step-by-step count for the CW derivation that follows. Let us just say that several steps are reduced to fewer and clearer steps. Most important is the
wave-natural insight that is gained and the wave mechanics that follows.
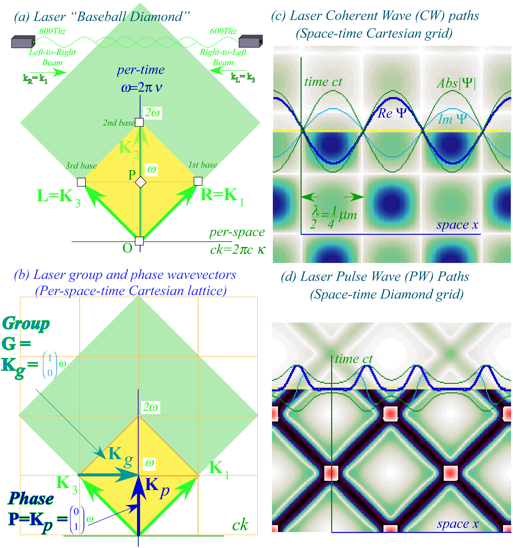
Fig. 2.1. Laser lab view of 600Thz CW and PW light waves in
per-space-time (a-b) and space-time (c-d).
In
fact, we could claim that a CW derivation takes zero steps. It is already done by a 2-CW wave
pattern in Fig. 2.2c that automatically produces an Einstein-Lorentz-Minkowski[vi]
grid of space-time coordinates. Still we need logical steps drawn in Fig.
2.2a-b that redo the Cartesian grid in Fig. 2.1 just by Doppler shifting each
baseline one octave according to c-axiom
(1.1) (“Stay on baselines!”)
and t-reversal axiom (1.2) (“If 1st
base increases by one octave, 3rd base decreases by the same.”)
So
Fig. 2.2 is just Fig. 2.1 seen by atoms going right-to-left fast enough to
double both
frequency õ=Ě/2ð and wavevector ck of the
vector R on 1st base (while halving
vector L on 3rd base to obey (1.2).)
R=K1=( ck′1,Ě′1)= Ě(2,2)
(2.5a) L=K3=( ck′3,Ě′3 )= Ě(-1/2, 1/2) (2.5b)
The atom sees
head-on R-beam
blue-shift to frequency õ1′=2õ=Ě1′/2ð=1200THz(UV)
by doubling green õ1=Ě/2ð=õ3=600THz. It also sees the tail-on L-beam red-shift by half to õ3′=õ/2=Ě3′/2ð=300THz(IR).
The
phase vector Kphase and group vector Kgroup are plotted in (ck′,Ě′)-space in Fig. 2.2b.
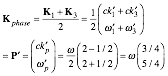 (2.6a)
(2.6a) 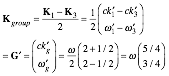 (2.6b)
(2.6b)
Phase velocity
is the inverse of group velocity in units of c, and V′group is minus the atoms’ velocity!
![]() (2.7a)
(2.7a) ![]() (2.7b)
(2.7b)
Velocity u=V′group
=3c/5 is the atoms’ view
for a lab speed of zero had by laser standing nodes. It is the speed of the lasers’
group nodes (and its supporting lab bench!) relative to the atoms. Phase
velocity V′phase =5c/3 is the atoms’ view for a lab speed of infinity had by lasers’ real wave zeros. The x-zero lines are simultaneous in the laser
lab but not so in the atom-frame. x-lines
tip toward ct-lines in Fig. 2.2c.
Eqs.
(2.5-7) use a Doppler blue-shift factor b=2. If each “2”
is replaced by “b”
then Eq. (2.7b) yields a relation for the laser velocity u=V′group
relative to atoms in terms of their blue-shift b.
![]() (2.8a)
(2.8a)
Inverting this
gives the standard relativistic Doppler b
vs. u/c relations. ![]() (2.8b)
(2.8b)
It is remarkable
that most treatments of relativity first derive second order effects, time dilation and length
contraction. Doppler and asimultaneity shifts are first order in u but treated second. Setting 2=b in (2.6) using (2.8) gives vectors ![]() and
and ![]() with dilation
factor
with dilation
factor ![]() and asimultaneity factor a=uŠd/c. (So a and d may be derived first here, too, but in a
wavelike way.)
and asimultaneity factor a=uŠd/c. (So a and d may be derived first here, too, but in a
wavelike way.)
![]() (2.9a)
(2.9a) ![]() (2.9b)
(2.9b)
K-vector components d and a
(in Ě units) are Lorentz-Einstein (LE) matrix coefficients
relating atom- values (ck′,Ě′)
or x′,t′ to lab-values (ck,Ě) or x,t
based on lab unit vectors ![]() =
=![]() and
and ![]() =
=![]() in (2.2).
in (2.2).
The
new K-vectors define the new coordinate grid of white-line wave-zero paths in
space-time of Fig. 2.2c and, perhaps more importantly, the new (ck′,Ě′) coordinates in per-space time of Fig.
2.2b.
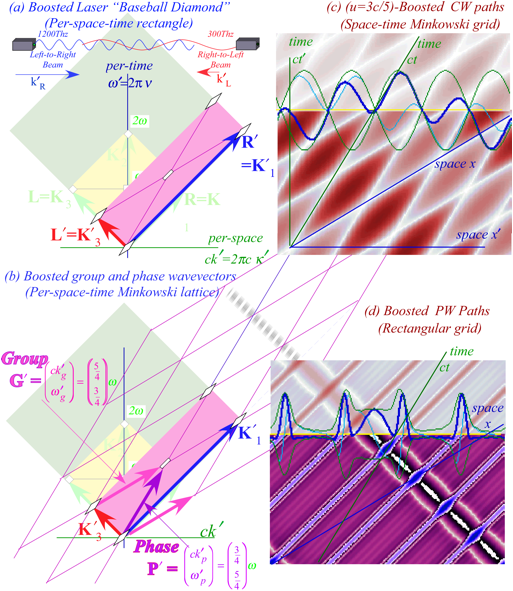
Fig. 2.2 Atom view of 600Thz CW and PW light waves in
per-spacetime (a-b) and space-time (c-d) boosted to u=3c/5.
Einstein’s
PW axiom “PW speed c is invariant,” might give the impression that pulses themselves are
invariant, but finite-Ä pulses in Fig. 2.2d clearly deform. Pulse speed is
invariant but each CW square in Fig. 2.3a deforms into a Minkowski-like rhombus
in Fig. 2.3b simply due to Doppler detuning beats.
Lorentz-Einstein transformations
The Lorentz[vii]-Einstein[viii]
per-spacetime and spacetime transformations follow from K-vectors (2.9).
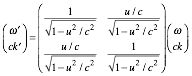 (2.10a)
(2.10a) 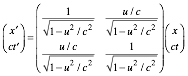 (2.10b)
(2.10b)
Wave K-vectors are bases for space-time and per-space-time. One symmetric LE matrix,
invariant to axis-switch (Ě,ck)![]() (ck,Ě),
applies to both. Conventional Ě−ordinate vs. ck-abscissa
per-space-time and ct-ordinate
vs. x-abscissa
space-time plots are used in Fig. 2.2 where
(ck,Ě),
applies to both. Conventional Ě−ordinate vs. ck-abscissa
per-space-time and ct-ordinate
vs. x-abscissa
space-time plots are used in Fig. 2.2 where ![]() =P=Kphase and
=P=Kphase and ![]() =G=Kgroup vectors serve as x-space and ct-time bases, respectively, and then also serve as Ě−and-ck-bases.
=G=Kgroup vectors serve as x-space and ct-time bases, respectively, and then also serve as Ě−and-ck-bases.
The
left and right pulse wave (PW) vectors L
and R in per-space-time Fig. 2.2a also define
left and right PW paths in space-time Fig. 2.2d. This holds in either
convention because L and R lie on 45° reflection planes that are
eigenvectors of an axis-switch (Ě,ck)![]() (ck,Ě) with
eigenvalues +1 and –1 while half-sum-and-difference vectors
(ck,Ě) with
eigenvalues +1 and –1 while half-sum-and-difference vectors ![]() and
and![]() simply switch (P
simply switch (P![]() G).
G).
Geometry of Lorentz-Einstein contraction-dilation
Fig.
2.3 compares wave path space-time coordinate lines for the laser lab in top
figure (a) and for the atom going right-to-left at speed u=3c/5 in bottom figure (b).
The
fast wave-phase zeros define the space-x
axis and gridlines in either view where they go at a speed of 5c/3 in the atom view and at infinite speed į
in the lab view.
The slow wave-group zeros define the time-ct
axis and gridlines in either view where they go at a speed of 3c/5 in the atom view and at zero speed 0 in
the lab view.
The
spatial separation of the slow wave-group zeros in Fig. 2.2c is 4/5 of the original 1/4ďm shown
separating the stationary wave zeros in Fig. 2.1c or Fig. 1.5a. That is the
Lorentz contraction factor
![]() .
.
The
inverse time dilation factor d=5/4 is the vertical height of the new “pitcher’s mound” P in Fig. 2.2a that was originally of unit
height in Fig. 2.1a. In space-time diamond of Fig. 1.5b the pitcher’s mound is 5/6
fs from origin or “home
plate” and that dilates by factor d=5/4 to 25/24 fs in Fig. 2.2c.
Detailed
geometry of relativistic quantities is given in later figures. (Fig. 5.1, 5.4,
and 5.5.)
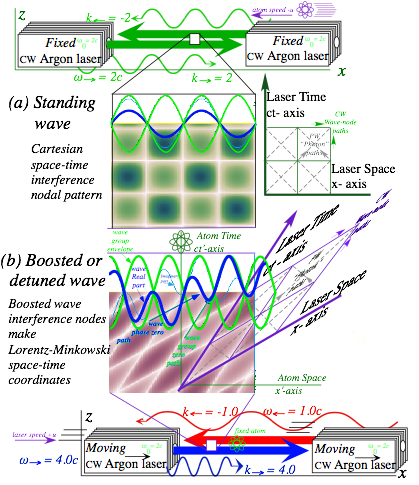
Fig. 2.3 Lasers make Cartesian
(x,ct)-wave frame for themselves and Minkowski (x′,ct′)-frame for atom.
Should
relativity continue to be taught by imagining monstrous frames, mirrors, and
smoke to trace bouncing “photon bunches” using clanking clocks carefully
synchronized by Swiss gnomes?
Perhaps, that
works as a humorous historical aside but current GPS systems and ultra high
precision pioneered by Evenson and coworkers begs our attention and critical
thought. Now as his students are achieving better than 17-figure time and
frequency measurements, it is time for theoretical pedagogy to sharpen Occam’s
razor accordingly. And, if there is history to review, it is first of Galileo
and Euclid.
Chapter 3. Invariance and Relative Phase: Galileo’s revenge
Einstein
relativity shows Galilean relativity, based on simple velocity sums and
differences, to be a 400 year-old approximation that fails utterly at high
speeds. Einstein also dethrones infinite velocity that is the one invariant velocity shared by
Galilean observers regardless of their (finite) velocity. In its place reigns a
finite velocity limit c=299,792,458ms-1 that is now the Einstein-Maxwell-Evenson
invariant speed.
So
it is remarkable that frequency sums and differences (1.10) simplify relativity
by using Galilean-like rules for angular velocities ![]() of light phases
of light phases ![]() . Frequency sums or differences
. Frequency sums or differences ![]() from interference terms like
from interference terms like ![]() between wave pairs
between wave pairs ![]() and
and ![]() are relative frequencies (beat notes, overtones, etc.) subject only to
simple addition and subtraction rules that are like Galileo’s rules for linear
velocity. Simple angular phase principles deeply underlie modern physics, and
so far there appears to be no c-like
speed limit for an angular velocity Ě.
are relative frequencies (beat notes, overtones, etc.) subject only to
simple addition and subtraction rules that are like Galileo’s rules for linear
velocity. Simple angular phase principles deeply underlie modern physics, and
so far there appears to be no c-like
speed limit for an angular velocity Ě.
Phase
principles have electromagnetic origins. Writing oscillatory wave functions
using real and imaginary parts is used to study AC phenomena or harmonic
oscillators in Unit 4. Real part q
of oscillator amplitude q+ip=![]() is its position q=AcosĚt.
Imaginary part p=AsinĚt is
oscillator velocity v =-AĚ sinĚt in
units of angular frequency Ě. Positive Ě gives a clockwise rotation like that of classical phase
space or analog clocks, so a minus sign in a conventional
is its position q=AcosĚt.
Imaginary part p=AsinĚt is
oscillator velocity v =-AĚ sinĚt in
units of angular frequency Ě. Positive Ě gives a clockwise rotation like that of classical phase
space or analog clocks, so a minus sign in a conventional![]() phasor serves to remind us that wave
frequency Ě
defines
our clocks and wavevector k=Ě/c defines our meter sticks. (Recall Fig. 1.10.5 and Fig. 4.2.1.)
phasor serves to remind us that wave
frequency Ě
defines
our clocks and wavevector k=Ě/c defines our meter sticks. (Recall Fig. 1.10.5 and Fig. 4.2.1.)
A
plane wave of wavevector k in Fig.
3.1 is drawn as a phasor array, one ![]() for each location x. A plane wave advances in time according
to
for each location x. A plane wave advances in time according
to ![]() at phase velocity V=Ě/k.
Similar convention and notation are used for light waves and for quantum matter
waves, but only light waves have physical units, vector potential A and electric E-field, defining their real and imaginary
parts. While classical laser wave phase is observable, only relative phase of a quantum wave Ņ appears to be so.
at phase velocity V=Ě/k.
Similar convention and notation are used for light waves and for quantum matter
waves, but only light waves have physical units, vector potential A and electric E-field, defining their real and imaginary
parts. While classical laser wave phase is observable, only relative phase of a quantum wave Ņ appears to be so.
The
concept of relative phase (and frequency) arises in classical or quantum
interference where a sum of two waves ![]() and
and![]() may be represented at each position x by a vector sum of a phasor-A with a
phasor-B as in Fig. 3.1a. (Fig. 3.1 has a sum of 12 phasors, one for each each x-point.) The result is a clockwise race around a
track between the faster one, say A-phase
may be represented at each position x by a vector sum of a phasor-A with a
phasor-B as in Fig. 3.1a. (Fig. 3.1 has a sum of 12 phasors, one for each each x-point.) The result is a clockwise race around a
track between the faster one, say A-phase
![]() of angular speed -ĚA, and the slower B-phase
of angular speed -ĚA, and the slower B-phase
![]() of angular speed -ĚB as sketched in Fig. 3.1b.
of angular speed -ĚB as sketched in Fig. 3.1b.
Galilean
relativity of phase angular velocity holds if the phase wave is governed by
linear equations of motion such as Maxwell’s equations. Very precise
measurements of en vacuo light have verified this so far and Einstein relativity is
a consequence. You might say this is Galieo’s revenge!
Fig. 3.1 Wave phasor addition. (a) Each phasor in a wave
array is a sum (b) of two component phasors.
(c) In phasor-relative views either A or else B is fixed. An
evolving sum-and-difference rectangle is inscribed in the (dashed) circle of
the phasor moving relative to the fixed one.
Geometry of relative phase
When
A passes B the sum is a maximum or beat that then subsides to a minimum or node when A is on the opposite side of the
track from B. If amplitude magnitudes |A| and |B| are equal as they are in Fig.
3.1, then the wave node is a wave zero that defines one of the group G-lines in WZ coordinates of Fig. 1.4
through Fig. 2.2. The relative angular velocity![]() (beat angular frequency) is the angular
rate at which A passes B. A-B passings occur ä times (per sec.) where ä is Ä divided by track length 2ð.
(beat angular frequency) is the angular
rate at which A passes B. A-B passings occur ä times (per sec.) where ä is Ä divided by track length 2ð.
![]() (3.1)
(3.1)
If
one could ride in an angular Galilean frame of phasor-B, then A would be seen
passing at angular speed Ä with frequency ä. Suppose instead, one could ride at
their average
angular speed ![]() .
.
![]() (3.2)
(3.2)
Then Galilean
arithmetic (which lasers given no reason to doubt in these matters) implies
that phasor A or B would each appear with a relative speed of plus-or-minus half their relative velocity.
![]() (3.3)
(3.3)
A
point of view relative to phasor B is shown by the first of Fig. 3.1c. A dashed
circle represents moving phasor A with ![]() on one diagonal of an inscribed rectangle
whose sides are the resultant sum
on one diagonal of an inscribed rectangle
whose sides are the resultant sum ![]() and difference
and difference ![]() . The other diagonal
. The other diagonal ![]() appears fixed. A companion figure has
appears fixed. A companion figure has ![]() appear fixed instead. Resultants in
either figure begin and end on a dashed circle traced by the phasor that is
moving relative to the other. A rectangle-in-circle is a key Euclidian element
of wave physics and is a key feature of a later figure (Fig. 3.3) that shows
the essence of wave interference geometry.
appear fixed instead. Resultants in
either figure begin and end on a dashed circle traced by the phasor that is
moving relative to the other. A rectangle-in-circle is a key Euclidian element
of wave physics and is a key feature of a later figure (Fig. 3.3) that shows
the essence of wave interference geometry.
The
half-sum and half-difference angles in Fig. 3.1b and frequencies (3.2) and
(3.3) appear in the interference formulas (1.10) that lead to relativistic
Lorentz-Einstein coordinate relations (2.10) and their WZ grid plots of
Minkowski coordinates in Fig. 2.2c. One key is the arithimetic
mean ![]() of phases that gives the geometric
mean
of phases that gives the geometric
mean ![]() of wave phasor amplitudes. The other key is the difference
mean
of wave phasor amplitudes. The other key is the difference
mean ![]() and that is the phase angle of a cross
mean
and that is the phase angle of a cross
mean![]() .
.
Euclidian means and rectangle-in-circle constructions underlie relativistic wave geometry as is shown below. This geometry also leads to the geometry of contact transformations in classical mechanics that exposes relations between classical and quantum mechanics in Ch. 5.
Any
number N of
transmitter-receivers (“observers” or “atoms” previously introduced) may each
be assigned a positive number b11, b21, b31, …that is its Doppler shift of a
standard frequency Ě1 broadcast by atom-1 and then received as
frequency Ěm1= bm1 Ě1 by an atom-m.
By definition a transmitter’s own shift is unity. (1=
b11) Also,
coefficient bm1 is independent of frequency since such geometric relations work as well on 1THz or 1Hz
waves as both waves march in lockstep to the receiver by Evenson’s CW axiom
(1.1). The production times of a single wavelength of the 1Hz-wave and 1012
wavelengths of the 1THz wave must be the same (1sec.), and so must be reception time for the
two waves since they arrive in lock step, even if ô
is shortened geometrically by 1/ bm1. Doppler is a geometric and multiplicative effect.
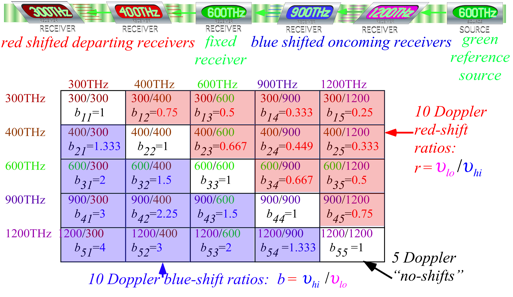
Fig. 3.2 Doppler shift b-matrix for a
linear array of variously moving receiver-sources.
If
atoms travel at constant speeds on a straight superhighway, then bm1 in (2.8a) tells what is the relative velocity
um1
of the mth
atomic receiver relative to the number-1
transmitter.
![]() (3.4)
(3.4)
The velocity um1 is positive if the mth atom goes toward transmitter-1 and sees a blue (bm1>1) shift, but if it moves away
um1 is negative
so it sees a red (bm1<1) shift. Transmitter-1 has no velocity relative to itself. (u11=0) Infinite blue (or red) shift bm1=į
(or bm1=0)
gives um1=c
(or um1=-c)
and this defines the range of parameters. The bm1 are constant until atom-m passes atom-1 so relative velocity flips sign (![]() ). Doppler shift then inverts (
). Doppler shift then inverts (![]() ) as is consistent with axiom (1.2).
) as is consistent with axiom (1.2).
Suppose
now b12,
b22,
b32,
…are Doppler shifts of frequency Ě2 transmitted by the second atom and received by the mth atom as frequency Ěm2= bm2 Ě2. (Any atom (say the nth) may transmit, too.)
Ěmn= bmn Ěn (3.5a)
Recipients don’t
notice if atom-n just
passes on whatever frequency Ěnm came from atom-m. If frequency Ěn in (3.5a) is Ěn1= bn1 Ě1 that atom-n got
from atom-1 then
atom-m will not distinguish a direct Ěm1 from a perfect copy bmn bn1 Ě1 made by atom-n
from atom-1 and
then passed on to atom-m.
Ěm1 = bm1 Ě1= bmn bn1 Ě1 (3.5b)
A multiplication
rule results for Doppler factors and applies to light from atom-1 or any atom-p.
Ěmp/Ěp= bmp =
bmn bnp (3.5c)
An inverse
relation results from atom-p
comparing its own light to that copied by atom-n.
1= bpp =
bpn bnp
or: bpn =1/bnp (3.5d)
Notice
that copying or passing light means just that and does not include reflection
or changing +k to –k or any other direction. This presents a
problem for a receiver not in its transmitter’s (+k)-beam and certainly for atom-p
receiving its own beam. The relations (3.5) depend only on relative velocities
and not positions (apart from the problem that a receiver might be on the wrong
side of a transmitter).
An
obvious solution is to let the receiver overtake its transmitter or failing
that delegate a slave transmitter or receiver on its right side. Fig. 3.2 shows
N=5
receivers of a Ě3=600THz source whose various speeds produce a matrix of N(N-1)=20 Doppler shifted frequencies Ěmn and factors bmn.
Doppler rapidity and Euclid means business
Composition
rules (3.5c) suggest defining Doppler factors b=eĖ in terms of rapidity Ė=ln b.
bmp =
bmn bnp implies:
Ėmp =
Ėmn +Ėnp where:
![]() (3.6)
(3.6)
Rapidity
parameters Ėmn
mimic Galilean addition rules as do phase angles ö of wavefunctionss ei ö. Both Ė and ö are the parameters
that underlie relativity and quantum theory. In fact, by (3.4) rapidity Ėmn approaches the relative velocity parameter umn
/c between atom-m and atom-n
for speeds much less than c.
Rapidity is also convenient for astronomically large Doppler ratios bab since then the numerical value of Ėab =ln bab is much less than bab while umn
/c approaches 1 in a way
that is numerically inconvenient.
At
intermediate relativistic speeds the geometric aspects of Doppler factors
provide a simple and revealing picture of the nature of wave-based mechanics.
Pairs of counter moving continuous waves (CW) have mean values between a K-vector R=K1=(ck1,Ě1) going
left-to-right and an L=K3=(ck3,Ě3) going right-to-left. A key
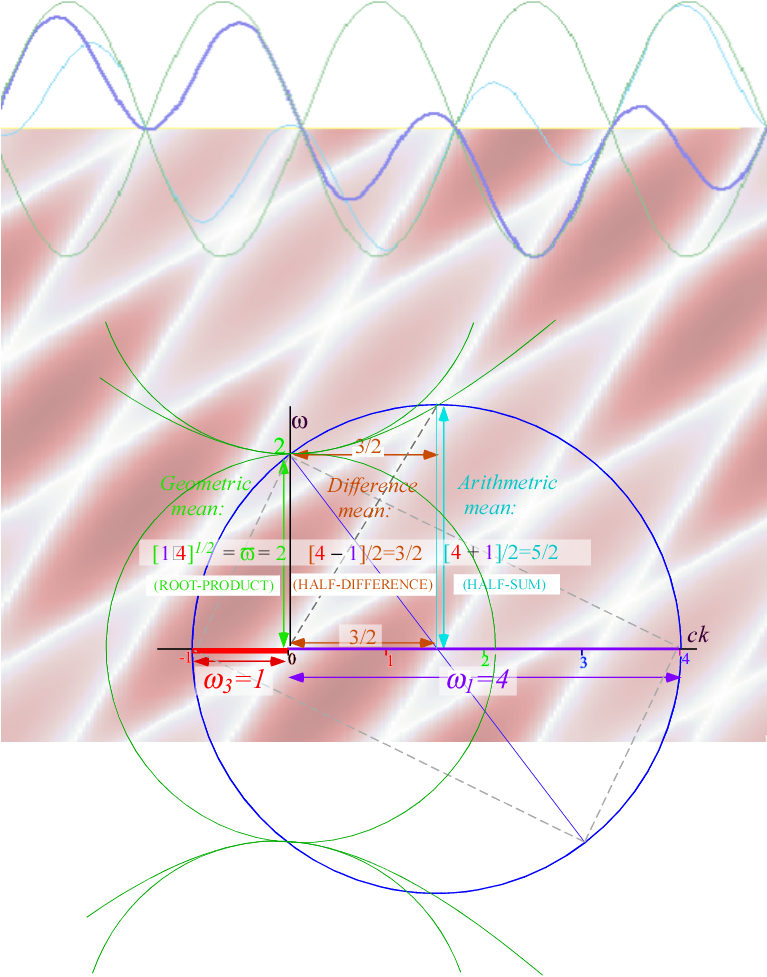
quantity is the geometric mean ϖ of
left and right frequencies.
![]() (3.7)
(3.7)
In Fig. 3.2a
frequency Ě1=1
or Ě3=4 is a
blue (b=e+Ė=2) or red (r=e−Ė=1/2) shift of mean ![]() .
.
![]() (3.8a)
(3.8a) ![]() (3.8b)
(3.8b)
In units of 2ð Š300THz,
frequency values Ě3=1
and Ě1=4 were
used in Fig. 2.2. Their half-sum 5/2
is their arithmetic mean.
That is the radius of the circle in Fig. 3.2b located a half-difference (3/2) from origin.
![]() (3.9a)
(3.9a) ![]() (3.9b)
(3.9b)
By (2.8) the
difference-to-sum ratio is the group or mean frame velocity-to-c ratio u/c=3/5 for b=2.
![]() (3.9c)
(3.9c) ![]() (3.9d)
(3.9d)
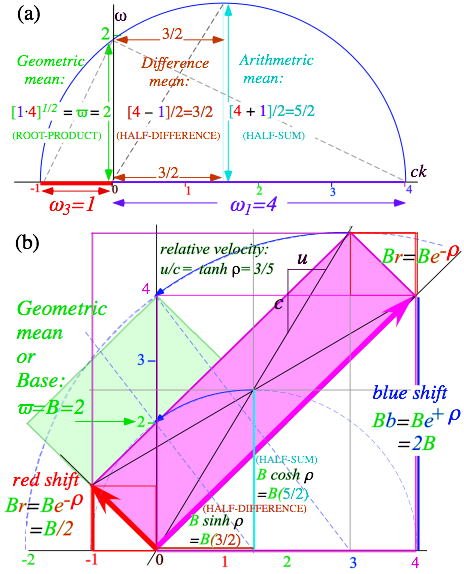
Fig. 3.3a Euclidian mean geometry for
counter-moving waves of frequency 1 and 4. (300THz units).
Fig. 3.3b Geometry for the CW wave coordinate axes in Fig.
2.2.
The
geometric mean (![]() ) in units of 2ð Š300THz
is the initial 600THz
green laser lab frequency used in Fig. 2.1. Diamond grid sections from Fig.
2.2b are redrawn in Fig. 3.3b to connect with the geometry of the Euclidian
rectangle-in-circle elements of interfering-phasor addition in Fig. 3.1c.
) in units of 2ð Š300THz
is the initial 600THz
green laser lab frequency used in Fig. 2.1. Diamond grid sections from Fig.
2.2b are redrawn in Fig. 3.3b to connect with the geometry of the Euclidian
rectangle-in-circle elements of interfering-phasor addition in Fig. 3.1c.
Various
observers see the single continuous wave frequencies Ě1
or Ě3
shifted to Ě′1=e+ĖĚ1 and Ě′3=e−ĖĚ3, that is, to values between zero and
infinity. But, because factor e−Ė cancels e+Ė, all will
agree on the 2-CW mean value ϖ =[Ě1Ě3]1/2=[Ě′1Ě′3]1/2. A 2-CW function has an invariant ϖ of its rest frame (Recall Fig. 2.2c) seen at velocity u=c(Ě1-Ě3)/( Ě1+Ě3). A single CW has no rest frame or
frequency since all observers see it going c
as in Fig. 1.1. To make a home frame, a single CW must marry another one!
Invariance of proper time (age) and frequency (rate of aging)
Space,
time, and frequency may seem to have an out-of-control fluidity in a wavy world
of relativism, so it is all the more important to focus on relativistic
invariants. Such quantities make ethereal light billions of times more precise
than any rusty old meter bar or clanking cuckoo clock.
It
is because of the time-reversal (1.2) and Evenson axiom (1.1) that product Ě1Ě3=ϖ2 is invariant to inverse blue-and-red
Doppler shifts b=e+Ė and r=e−Ė. It
means the blue-red shifted diamond in Fig. 3.3b or Fig. 2.2 has the same area R′xL′ as the original green “home field”
baseball diamond area RxL
drawn below it and in Fig. 2.1. Constant products Ě1Ě3=const. give families of hyperbolas.
|RxL|=2|GxP|=2|KgroupxKphase|=2|ϖ2cosh2Ė -ϖ2sinh2Ė|=2ϖ2
One hyperbola in
Fig. 3.4a intersects bottom point B=ϖ (“pitchers’mound”). The other hits 2B (2nd base). Each horizontal P -hyperbola is defined by the phase
vector P=Kphase or some multiple of P.
![]() (3.10a)
(3.10a)
Each vertical G -hyperbola is defined by the wave group
vector G=Kgroup
or some multiple of G.
![]() (3.10b)
(3.10b)
The
G-vectors serve as tangents to P-hyperbolas and vice-versa. The tangent
slope ![]() to any Ě(k) curve is a well known definition of
group velocity. Fig. 3.4b shows how
to any Ě(k) curve is a well known definition of
group velocity. Fig. 3.4b shows how ![]() of a P-hyperbola is equal to secant slope
of a P-hyperbola is equal to secant slope
![]() in Fig. 3.4a as defined in the u=Vgroup equation (2.7b) based on CW axioms.
in Fig. 3.4a as defined in the u=Vgroup equation (2.7b) based on CW axioms.
Phase
velocity ![]() =Vphase and its P-vector
is an axis-switch (Ě,ck)
=Vphase and its P-vector
is an axis-switch (Ě,ck)![]() (ck,Ě) of
(ck,Ě) of ![]() and its G-vector.
In conventional c-units Vgroup/c<1 and 1<Vphase/c are
inverses according to (2.7). (VphaseŠVgroup=c2)
and its G-vector.
In conventional c-units Vgroup/c<1 and 1<Vphase/c are
inverses according to (2.7). (VphaseŠVgroup=c2)
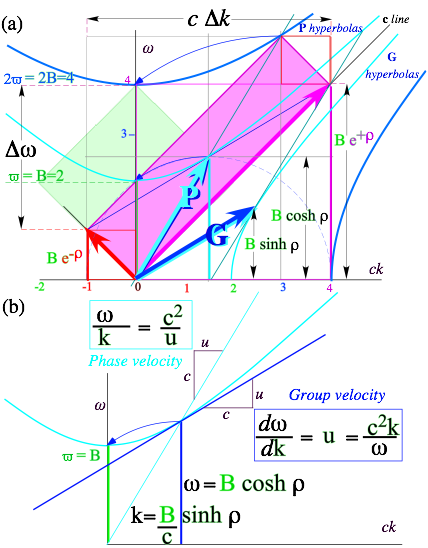
Fig. 3.4 (a) Horizontal G-hyperbolas
for proper frequency B=ϖ and 2B and
vertical P-hyperbolas for proper wavevector k. (b) Tangents for G-curves are
loci for P-curves, and vice-versa. Note: secant ÄĚ/Äk and tangent dĚ/dk are always
exactly equal.
Features
on per-space-time (ck,Ě)
plots of Fig. 3.3-Fig. 3.4 reappear on space-time (x,ct) plots as noted in Fig. 2.1 and Fig. 2.2.
A space-time invariant analogous to (3.10) is called proper-time
ô.
![]() (3.11)
(3.11)
It
conventional to locate oneself at (0,ct) or presume one’s origin x=0 is located on oneself. Then (3.11) reduces to time axis ct=cô. A colloquial
definition of proper time is age, a digital readout of one’s computer clock that all
observers may note. By analogy, ϖ is proper-frequency, a rate of aging or a digital readout on each of the
spectrometers in Fig. 3.2. Each reading is available to all observers.
![]() (3.12)
(3.12)
The same
hyperbolas (3.12) mark tics on the laser lab (Ě,ck), the atom frame (Ě′,ck′), or any
other frame.
The
proper frequency of a wave is that frequency observed after one Doppler shifts
the wave’s kinks away, that is, the special frequency ϖ seen in the
frame in which its wavevector is zero (ck=0) in (3.12). Hence a single CW has a proper frequency that
is identically zero (ϖ =0) by Evenson’s axiom (Ě=ck), so
single CW light cannot age. If we could go c
to catch up to light’s home frame then its phasor clocks would appear to stop.
Someone moving along a line of phasor clocks in Fig. 1.1c would always see the
same reading, but that would be an infinite Doppler shift that one can only
approach.
To
produce a nonzero proper frequency ϖ ≠0 requires interference of at least two
CW entities moving in different directions and this produces a standing wave
frame like Fig. 2.1c moving at a speed less than c
as shown in Fig. 2.2c. Matched CW-pairs of L
and R baselines frame a “baseball diamond” for
which the phase wavevector kp
in (2.2a) is zero. Then frame velocity u=Vgroup in (2.3b) is zero, too.
Fig. 3.5 shows the plots of per-spacetime “baseball diamond” coordinates for comparison of lab and atom frame views. While Fig. 3.5a is a “blimp’s-eye view” of the lab-frame diamond in Fig. 2.1, the atom frame view in Fig. 3.5b looks like the baseball field seen by a spectator sitting in the stands above the dugout. Nevertheless, identical hyperbolas are used to mark grids in either view.
Each
point on the lower hyperbola is a bottom point Ě′=B=2 (600THZ) for the frame whose relative velocity u′ makes it a Ě′-axis (k′=0)-point, and every (k′=0)-point
on the upper hyperbola is its bottom point Ě′=2B=4
(1200THZ), and so on for
hyperbolas of any given proper frequency value ϖ.
The same applies to space-time plots for which time ct′ takes the
place of per-time Ě′ and space x′ takes the place of per-space ck′. Then bottom
points are called proper time or ô-values from (3.11).
For single CW light the proper time must be constant since a single CW cannot age. It is a convention to make the baselines or light cone intersect at the origin in both time and space. This sets the baseline proper time constant ô to zero. Then invariants (3.11) reduce to baseline equations x=Īct or x′=Īct′ for all frames. The space-time light cone relations are in direct correspondence with the per-space-time light cone relations Ě=Īck or Ě′=Īck′ for zero proper frequency in all frames and are concise restatements of the Evenson CW axiom (1.1).
Fig. 3.5 Dispersion hyperbolas for 2-CW
interference (a) Laser lab view. (b)Atom frame view.
Chapter 4. Mechanics based on CW axioms
Each
of the 2-CW structures or properties discussed so far are due to relative
interference effects between pairs of 1-CW entities that, by themselves, lack
key 2-CW properties such as a proper invariant frequency ϖ, a rest
frame, or any speed below the mortally unattainable velocity of c. To acquire “mortal” properties requires
an interference encounter or pairing of 1-CW with another.
Now
we see how 2-CW interference endows other “mortal” properties such as classical
mass
and relativistic mechanics of energy-momentum that characterize a quantum matter wave.
Such endowment lies in P-hyperbola phase relations (3.10a) that in turn are due
to CW axioms (1.1) and (1.2).
![]() (4.1a)
(4.1a) ![]() (4.1b)
(4.1b) 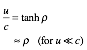 (4.1c)
(4.1c)
Hyperbola in
Fig. 3.4 has bottom B=ϖ and P-vector
components (Ěp,ckp) with tangent slope u/c at P.
At low group velocity (u=c)
the rapidity Ė
approaches u/c. Then
Ěp
and kp are simple functions of u.
![]() (4.2a)
(4.2a) ![]() (4.2b)
(4.2b)
The Ěp
and
kp fit
Newtonian-energy E and
Galilean-momentum p. Is
that a coincidence? Perhaps, not!
![]() (4.3a)
(4.3a) ![]() (4.3b)
(4.3b)
Wave Ě and k results (4.2), scaled by a single factor s=Mc2/B,
match classical E and p definitions (4.3).
![]() (4.4a)
(4.4a) ![]() (4.4b)
(4.4b)
In
Newton’s mechanics, only energy difference ÄE counts,
so he might ignore the term E=const.
(4.3a). But, in (4.4a) that const.=sB
is the proper phase carrier-frequency value B=ϖ at hyperbola bottom B in Fig. 3.4b. That is scaled by s=Mc2/B to sB=sϖ in Fig. 4.1. It is Einstein rest energy
and not ignorable!
const.= sB = Mc2 = sϖ (4.4c)
ϖ-mass-energy
equivalence is a huge idea due to Einstein (1905) and Planck (1900). k-vector-momentum equivalence by DeBroglie
came later (1920). CW results (4.1) give both directly and exactly.
![]() (4.5a)
(4.5a) ![]() (4.5b)
(4.5b)
Scale
factor s in
Planck[ix]
E=sĚ or DeBroglie[x]
p=sk laws is found experimentally. The lowest
observed s-value
is Planck angular constant h=1.05Š10-34JŠs. That is Planck’s axiom E=hĚ=õ for N=1. Integer
is Planck’s optical quantum number later called photon-number. At first, Planck regretted his 1900
axiom
E=õ. It seems inconsistent with Ě 2-dependence of classical oscillator
energy E=A2Ě2. In 1905, Einstein resolved this. A key
idea is quantized amplitude AN=√(hN/õ). (Even
amplitude is wavy!)
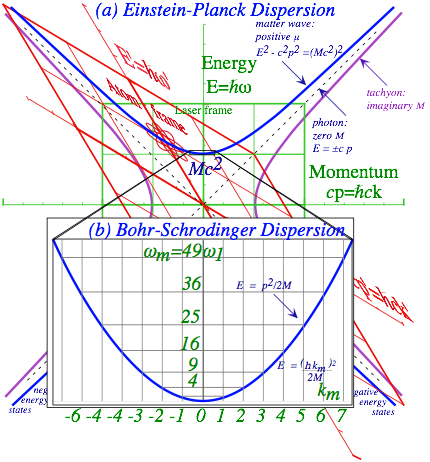
Fig. 4.1 Energy vs. momentum dispersion functions including mass M, photon, and tachyon.
(a) Relativistic (Einstein-Planck-deBroglie) case: ()2=E2-(cp)2 = 1 or ď2=Ě2-(ck)2 = 1/h2.
(b) Non-relativistic (Bohr-Schrodinger-deBroglie) case: Ā =-(1/2M)p2 or Ě =hk2/2M
Quantized cavity modes and “fuzzy” hyperbolas
Cavity boundary
conditions “1st-quantize”
classical wave mode variables (Ěn,kn) so as to have discrete numbers n=1,2,3,… of half-wave anti-nodes that fit in a
cavity of length-l as shown at the top of Fig. 4.2.
kn=Ļ/Ďn= nŠĻ/l (4.6a) Ěn=c kn = c nŠĻ/l (4.6b)
Planck’s axiom “2nd-quantizes” each fundamental mode frequencyĚn
to have discrete quantum numbers Nn=0,1,2,3,… of photons. Each level EN(n)=hNnĚn labels a hyperbola in Fig. 4.2 whose
number n of
anti-nodes and N of
photons is invariant.
This lends object-permanence
to cavity “light particles” or photons.
As
discussed in Ch. 6, laser waves are coherent state combinations of N-photon states that have semi-classical
properties that include well-defined wave phase. One “fuzzy” hyperbola of
uncertain N and
mass-energy replaces the ladders in Fig. 4.2. This is a kind of 2nd
Occam-razor cut after the 1st cut of PW into CW. As discussed in Ch.
6, it resolves CW into coherent combinations of “2nd-quantized” photons.
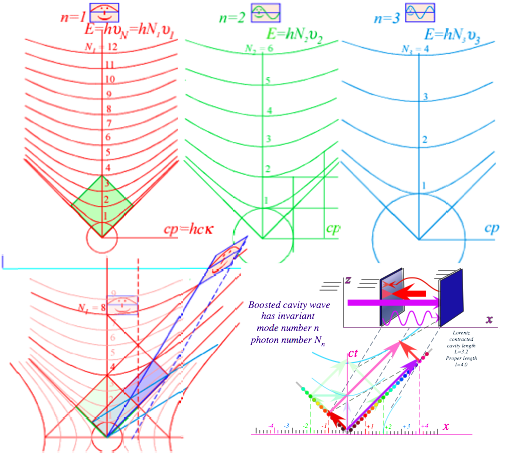
Fig. 4.2 Optical cavity energy
hyperbolas for mode number n=1-3 and photon number N=0, 1, 2,....
Alternative definitions of wave mass
If
mass or rest energy is due to proper phase frequency ϖ, then a
quantum matter wave has mass without invoking hidden Newtonian “stuff.” With
Occam logical economy, 2-CW light led to exact mass-energy-momentum (Ě,k) relations (4.5) and not just low-speed
classical ones (4.3). Now we see how 2-CW results expose some salient
definitions of mass or matter that a classical theory might overlook.
First,
the Einstein-Planck wave frequency-energy-mass equivalence relation (4.4c)
ascribes rest mass Mrest to a scaled proper carrier frequency sϖ /c2.
The scale factor s is
Planck’s s=h for N quanta.
![]() (4.7)
(4.7)
For rest
electron mass me =9.1Š10-31kg or Mp =1.67Š10-27kg of a proton, the proper frequency times N=2 is called zwitterbevegun (“trembling motion”) and is as
mysterious as it is huge. (Electron rest frequency ϖe = me c2/h =7.76Š10+20(rad)s-1 is the Dirac (e+e−)-pair
production[xi]
threshold as discussed in Ch. 8.)
Second, we define momentum-mass Mmom by ratio p/u of
momentum (4.5b) to velocity u.
(Galileo’s p=Mmomu)
Now Mmom varies as ![]() at high rapidity Ė but approaches
invariant Mrest
as
at high rapidity Ė but approaches
invariant Mrest
as![]() .
.
 (4.8)
(4.8)
Frame velocity u is wave group velocity and the Euclid mean construction of Fig. 3.3a shows u is the slope of the tangent to dispersion function Ě(k). A derivative of energy (4.5a) verifies this once again.
![]() (4.9)
(4.9)
Third,
we define effective-mass
Meff as ratio![]() =F/a=dp/du of momentum-change
to acceleration. (Newton’s F=Meffa)
Meff varies as
=F/a=dp/du of momentum-change
to acceleration. (Newton’s F=Meffa)
Meff varies as ![]() at high rapidity Ė but also approaches Mrest as
at high rapidity Ė but also approaches Mrest as![]() .
.
 (4.10)
(4.10)
Effective mass is h divided by the curvature of dispersion function Ě(k), a general quantum wave mechanical result. Geometry of a dispersion hyperbola Ě=BcoshĖ is such that its bottom (u=0) radius of curvature (RoC) is the rest frequency B=Mrestc2/h, and this grows exponentially toward į as velocity u approaches c. The 1-CW dispersion (Ě=Īck) is flat so its RoC is infinite everywhere and so is photon effective mass Meff(č)=į. This is consistent with the (All colors go c)-axiom (1.1). The other extreme is photon rest mass Mrest(č)=0. Between these extremes, photon momentum-mass depends on CW color Ě.
Mrest(č)=0 (4.11a) Mmom(č)=p/c=hk/c=hĚ/c2 (4.11b) Meff(č)=į (4.11c)
For Newton this would confirm light’s “fits” to be crazy to
the point of unbounded schizophrenia. A
2-CW 600THz cavity has zero total momentum
p, but each photon adds a
tiny mass Mč to it.
Mč=hĚ/c2=Ě (1.2Š10-51)kgŠs= 4.5Š10-36kg (for:
Ě = 2ðŠ600THz )
In contrast, a 1-CW state has no rest
mass, but 1-photon momentum (4.5b) is a non-zero value
pč=Mč c.
pč=hk=hĚ/c=Ě (4.5Š10-43)kgŠm=1.7Š10-27kgŠmŠs-1 (for:
Ě = 2ðŠ600THz )
This p=Mc resembles Galilean relation p=Mu in (4.3b) and is perhaps another case of Galileo’s revenge!
Absolute vs. relative phases: Method in madness
Probably Newton would find a CW theory to be quite mad. Claiming that heavy hard matter owes its properties to rapid hidden “carrier” phase oscillations would not elicit a Newtonian invitation to the Royal Society but rather to a lunatic asylum. Even though CW results (4.2) give Newtonian axioms (4.3) at low speeds, the result would seem to fail at high speeds where exact results (4.5) sag below Newton’s. Also, having an enormous constant Mc2 be part of energy would, in 1670, seem insanely meaningless.
But, in 1905[xii] Einstein relations appear with both Mc2 and energy sag. Now Einstein’s classical training left him leery of hidden quantum wave phases with dicey interpretations of intensity Į∗Į as probability. Also, he may have asked why observable results depend on a square Į∗Į=|Į| that kills that overall phase frequency, seemingly losing the one quantity that represents (or is) the total mass-energy.
Square
|Į| of a 2-CW Į=eia+eib
loses phase factor![]() leaving
group functions
leaving
group functions ![]() of differences
of differences
![]() or
or
![]() of 1st or 3rd base frequencies or k-vectors.
Group beat frequency
of 1st or 3rd base frequencies or k-vectors.
Group beat frequency ![]() is zero in the rest frame of Fig. 2.1c where it is a stationary wave. In Fig.
2.2c or any other frame, |Į|
is not stationary but is observed to have velocity Vgroup≠0. Fourier sums of m=3 or more terms
is zero in the rest frame of Fig. 2.1c where it is a stationary wave. In Fig.
2.2c or any other frame, |Į|
is not stationary but is observed to have velocity Vgroup≠0. Fourier sums of m=3 or more terms ![]() may have multiple beats in
may have multiple beats in ![]() as in Fig. 2.2d.
as in Fig. 2.2d.
![]() (4.12)
(4.12)
With
![]() observable difference
observable difference![]() or beat
notes, P
cannot rest in any frame. Differences or derivatives are observable while
absolute Į-frequency stays hidden until two quantum objects interfere.
Then new beats arise from differences between the two absolute frequencies and
others. A new absolute phase (not in |Į|) is the sum of all. But, we can only
observe beats of relative frequency! That may be a quantum version of
Einstein’s popularized saw, “It’s all relative.” Phase velocity
escapes with its Galilean arithmetic intact in Fig. 3.1, but here it finally
surrenders its absolutes to relativism.
or beat
notes, P
cannot rest in any frame. Differences or derivatives are observable while
absolute Į-frequency stays hidden until two quantum objects interfere.
Then new beats arise from differences between the two absolute frequencies and
others. A new absolute phase (not in |Į|) is the sum of all. But, we can only
observe beats of relative frequency! That may be a quantum version of
Einstein’s popularized saw, “It’s all relative.” Phase velocity
escapes with its Galilean arithmetic intact in Fig. 3.1, but here it finally
surrenders its absolutes to relativism.
Total phase gives total energy E or momentum p, but differentials are what one feels through work ÄE or impulse Äp. Invariant quantities like ϖ and Mrest depend on total phase but intensity (4.12) has only differentials Äkij or relative beats ÄĚij. Among frame-dependent relative quantities are group velocity u (4.9), Mmom (4.8), and Meff (4.10), but rest mass Mrest (4.4c) is a frame-invariant absolute quantity. Also note that Mmom and Meff approach Mrest at zero velocity. Now |Į| may register an ϖ beat with a DC (static Ě0=0) wave, but lack of resonance confines (Ě0=0)-carrier waves to beat only locally.
Phase
frequency Ěp in a quantum wave ![]() is fast and silent like a carrier frequency of radio wave. Group frequency Ěg is like the audible
signal, much slower and heard in resonant beats Ěa −Ěb involving carrier and
receiver. Atomic “carrier” frequencies Ěp=Mc2/h
due to rest mass are enormous as are those of atomic measuring devices that
play the role of “receivers” in quantum experiments. Measurement involves
resonant contact of an atom and devices that horse-trade beats at truly huge
frequencies.
is fast and silent like a carrier frequency of radio wave. Group frequency Ěg is like the audible
signal, much slower and heard in resonant beats Ěa −Ěb involving carrier and
receiver. Atomic “carrier” frequencies Ěp=Mc2/h
due to rest mass are enormous as are those of atomic measuring devices that
play the role of “receivers” in quantum experiments. Measurement involves
resonant contact of an atom and devices that horse-trade beats at truly huge
frequencies.
One way to avoid huge Mc2/h-related phase frequencies is to ignore them and approximate the relativistic equation E=Mc2coshĖ of (4.5a) by the Newtonian approximation (4.4a) that deletes the big rest-energy constant sB=Mc2. The exact energy (4.5a) that obeys CW axioms (1.1) is rewritten in terms of momentum (4.5b) below to give a Bohr-Schrodinger (BS) approximation (4.14) with Mc2 deleted.
![]() (4.13)
(4.13)
![]() (4.14)
(4.14)
If only frequency difference affect observation based on |Į| (4.12), the BS claim is that energy origin may be shifted from (E=Mc2, cp=0) to (E=0, cp=0). (Frequency is relative!) Hyperbola (4.13) in Fig. 4.1a, for u way less then c, approaches the BS parabola (4.14) in Fig. 4.1b. That is the only E(p) Newton knew.
Group velocity u=Vgroup![]() of (4.9) is a relative or differential
quantity so origin shifting does not affect it. However, phase velocity
of (4.9) is a relative or differential
quantity so origin shifting does not affect it. However, phase velocity![]() =Vphase
is greatly reduced by deleting Mc2 from E=hĚ. It slows from Vphase=c2/u
that is always faster than light to a sedate sub-luminal speed of Vgroup/2. Having Vphase
go slower than Vgroup is an unusual situation but one that
has achieved tacit approval for BS matter waves.[xiii]
The example used in Fig. 1.6 of Ch. 1 is a 2-CW BS matter wave exhibiting this
low Vphase.
=Vphase
is greatly reduced by deleting Mc2 from E=hĚ. It slows from Vphase=c2/u
that is always faster than light to a sedate sub-luminal speed of Vgroup/2. Having Vphase
go slower than Vgroup is an unusual situation but one that
has achieved tacit approval for BS matter waves.[xiii]
The example used in Fig. 1.6 of Ch. 1 is a 2-CW BS matter wave exhibiting this
low Vphase.
Standard Schrodinger quantum mechanics, so named in spite of Schrodinger‘s protests[xiv], uses Newtonian kinetic energy (4.14) or (4.3) with potential ϕ (as the const.-term) to give a BS Hamiltonian.
H=p2/2M
+ ϕ or: hĚ= h2k2/2M
+ 〈ϕ〉 (4.15)
The CW approach
to relativity and quantum exposes some problems with such approximations.
First,
a non-constant potential ϕ must have a vector potential A so that (ϕ,cA) transform like (Ě,ck) in
(2.10a) or (ct,x) in
(2.10b) or as (E,cp) with
scaling laws p=hk and E=hĚ. Transformation
demands equal powers for frequency (energy) and wavevector (momentum) such as
the following.
(E- ϕ)2=(p-cA)2/2M+Mc2 or:
(hĚ-〈ϕ〉)2=
(hk-cA)2/2M+Mc2 (4.16)
Also, varying
potentials perturb the vacuum so single-CW’s may no longer obey axioms (1.1-2).
Diracs’s
elegant solution obtains Īpairs of hyperbolas (4.13) or (4.16) from
avoided-crossing eigenvalues of 4x4 Hamiltonian matrix equations with
negative frequency hyperbolas. The negative-Ě hyperbolas in Fig.
4.1 are (conveniently) hidden by the BS approximate dispersion parabola.
Dirac’s
ideas require three-dimensional wavevectors and momenta. But first, fundamental
Lagrangian-Hamiltonian geometric relations of quantum phase and frequency
relate relativistic classical and quantum mechanics in the following Ch. 5.
These relations expose more of the logic of phase-based Evenson axiom (1.1),
Doppler T-symmetry
axiom (1.2), and Euclid frequency means in Fig. 3.3.
Chapter 5. Classical vs. quantum mechanics
The
CW-spectral view of relativity and quantum theory demonstrates that wave phase
and in particular, optical phase, is an essential part of quantum theory. If
so, classical derivation of quantum mechanics might seem about as viable as
Aristotelian derivation of Newtonian mechanics.
However,
the 19th century mechanics of Hamilton, Jacobi, and Poincare developed the concept of action
S defined variously by area ![]() in phase-space or a Lagrangian time
integral
in phase-space or a Lagrangian time
integral ![]() . The latter action definition begins
with the Legendre transformation of Lagrangian L
and Hamiltonian H
functions.
. The latter action definition begins
with the Legendre transformation of Lagrangian L
and Hamiltonian H
functions.
![]() (5.1a)
(5.1a)
L is an
explicit function of x and
velocity ![]() while the H
is explicit only in x and
momentum p.
while the H
is explicit only in x and
momentum p.
![]() (5.1b)
(5.1b) ![]() (5.1c)
(5.1c) ![]() (5.1d)
(5.1d) ![]() (5.1e)
(5.1e)
Multiplying by dt gives the differential Poincare invariant dS and its action
integral ![]() .
.
![]() (5.2a)
(5.2a) ![]() (5.2b)
(5.2b)
Planck-DeBroglie
scaling laws p=hk and E=hĚ (4.5) identify action S as scaled quantum phase hÖ.
![]() (5.3a)
(5.3a) ![]() (5.3b)
(5.3b)
If
action dS
or phase dÖ is integrable, then Hamilton-Jacobi equations
or (k,Ě)
equivalents hold.
![]() (5.4a)
(5.4a) ![]() (5.4b)
(5.4b) ![]() (5.4c)
(5.4c) ![]() (5.4d)
(5.4d)
Phase-based relations (5.4c-d) define angular frequency Ě and wave number k. The definition (3.8) of wave group velocity is a wave version of Hamilton’s velocity equation (5.1e).
![]() equivalent to:
equivalent to: ![]()
The coordinate Hamilton derivative equation relates to wave
diffraction by dispersion anisotropy. ![]() equivalent to:
equivalent to: ![]()
Classical HJ-action theory was intended to analyze families of trajectories (PW or particle paths), but Dirac and Feynman showed its relevance to matter-wave mechanics (CW phase paths) by proposing an approximate semi-clasical wavefunction based on the Lagrangian action as phase.
![]() (5.5)
(5.5)
The
approximation symbol (![]() )
indicates that only phase but not amplitude is assumed to vary here. An x-derivative (5.4a) of semi-classical wave
(5.5) has the p-operator form in standard BS quantum
theory.
)
indicates that only phase but not amplitude is assumed to vary here. An x-derivative (5.4a) of semi-classical wave
(5.5) has the p-operator form in standard BS quantum
theory.
![]() (5.6a)
(5.6a) ![]() (5.6b)
(5.6b)
The time derivative is similarly related to the Hamiltonian operator. The HJ-equation (5.4b) makes this appear to be a BS Hamiltonian time equation.
![]() (5.7a)
(5.7a) ![]() (5.7b)
(5.7b)
However, these
approximations like the BS approximations of (4.14) ignore relativity and lack
economy of logic shed by light waves. The Poincare phase invariant of a
matter-wave needs re-examination.
Contact transformation geometry of a relativistic Lagrangian
A
matter-wave has a rest frame where x′=0=k′ and its phase Ö = kx-Ě t
reduces to −ďô,
a product of its proper frequency ď =![]() (or
Mc2/h)
with proper time t ′=ô. Invariant differential dÖ is reduced, as well,
using the Einstein-Planck rest-mass energy-frequency equivalence relation
(4.4c) to rewrite it.
(or
Mc2/h)
with proper time t ′=ô. Invariant differential dÖ is reduced, as well,
using the Einstein-Planck rest-mass energy-frequency equivalence relation
(4.4c) to rewrite it.
dÖ
= kdx−Ě dt=−ď dô
= -(Mc2/h)
dô. (5.8)
ô-Invariance (2.21)
or time dilation in (2.10b) gives proper dô in terms of velocity ![]() and lab dt.
and lab dt.
dô = dt √(1-u2/c2) )=dt sech Ė (5.9)
Combining definitions for action dS=Ldt (5.2) and phase dS = hdÖ (5.3) gives the Lagrangian L.
L =−hďô = -Mc2√(1-u2/c2)= -Mc2sech Ė (5.10)
Fig. 5.1 plots this free-matter Lagranian L next to its Hamiltonian H using units for which c=1=M.
Fig. 5.1. Geometry of contact
transformation between relativistic (a) Hamiltonian (b) Lagrangian
Relativistic
matter Lagrangian (5.10) is a circle (Fig. 5.1b). L-values ![]() and
and ![]() in
Fig. 5.1 are contact Legendre transforms of H-values
in
Fig. 5.1 are contact Legendre transforms of H-values ![]() and
and![]() of
Hamiltonian hyperbola in Fig. 5.1a. Abscissa p and ordinate H of a point P
in plot (a) gives negative intercept -H and
slope p of tangent HQ contacting the
transform point Q in plot (b) and vice-versa. (Contact geometry is
really wave-action-energy mechanics.)
of
Hamiltonian hyperbola in Fig. 5.1a. Abscissa p and ordinate H of a point P
in plot (a) gives negative intercept -H and
slope p of tangent HQ contacting the
transform point Q in plot (b) and vice-versa. (Contact geometry is
really wave-action-energy mechanics.)
If
![]() ,
Lagrange kinetic energy
,
Lagrange kinetic energy ![]() is Hamilton
is Hamilton ![]() .
Then circle L and
hyperbola H both
approximate a Newtonian parabola at low speed u<<c. But, as
.
Then circle L and
hyperbola H both
approximate a Newtonian parabola at low speed u<<c. But, as![]() the
L-circle rises above the
parabola and the H-hyperbola
sags below it and instead approaches contacting c-asymptote in Fig. 5.1.
the
L-circle rises above the
parabola and the H-hyperbola
sags below it and instead approaches contacting c-asymptote in Fig. 5.1.
Action
integral S=ļLdt
is to be minimized. Feynman’s interpretation of S
minimization is depicted in Fig. 5.2. A mass flies so that its “clock” ô is maximized.
(Proper frequency![]() is constant for fixed rest mass, and so minimizing −ďô means maximizing +ô.)
An interference of Huygen wavelets favors stationary and extreme phase. This
favors the fastest possible clock as is sketched in Fig. 5.3.
is constant for fixed rest mass, and so minimizing −ďô means maximizing +ô.)
An interference of Huygen wavelets favors stationary and extreme phase. This
favors the fastest possible clock as is sketched in Fig. 5.3.
Feynman described families of classical paths or rays fanning out from each space-time point on a wavefront of constant phase Ö or action S. Then, according to an application of Huygen's principle to matter wave, new wavefronts are continuously built in Fig. 5.3 through interference from “the best” of all the wavelets emanating from a multitude of source points on each preceding wavefront. Thus classical momentum p=∇S by (5.4a) for the “best” ray ends up normal to each wavefront.
The “best” are so-called stationary-phase rays that are extremes in phase and thereby satisfy Hamilton's Least-Action Principle requiring that ļLdt is minimum for “true” classical trajectories. This in turn enforces Poincare' invariance by eliminating, by de-phasing, any “false” or non-classical paths because they do not have an invariant (and thereby stationary) phase. “Bad rays” cancel each other in a cacophonous mish-mash of mismatched phases. Each Huygen wavelet is tangent to the next wavefront being produced. That contact point is precisely on the ray or true classical trajectory path of minimum action and on the resulting “best” wavefront. Time evolution from any wavefront to another is thus a contact transformation between the two wavefronts described by the geometry of Huygens Principle.
Thus a Newtonian clockwork-world appears to be the perennial cosmic gambling-house winner in a kind of wave dynamical lottery on an underlying wave fabric. Einstein’s God may not play dice, but some persistently wavelike entities seem to be gaming at enormous Mc2/h-rates down in the cellar!
It is ironic that Evenson and other metrologists have made the greatest advances of precision in human history, not with metal bars or ironclad classical mechanics, but by using the most ethereal and dicey stuff in the universe, light waves. This motivates a view of classical matter or particle mechanics that is more simply and elegantly done by its relation to light and its built-in relativity, resonance, and quantization that occurs when waves are subject to boundary conditions or otherwise confined. While Newton was complaining about “fits” of light, that crazy stuff was just trying to tell him something!
Derivation of quantum phenomena using a classical particle paradigm seems silly now. If particles are made by waves, optical or otherwise, rather than vice versa as Newton believed, the case is closed. Also, CW trumps PW as CW symmetry axioms (1.1-2) derive classical results (4.4) while giving exact relations (4.5) for relativity and quantum theory tossed into the bargain. Such Occam economy is found lacking on a PW path from Newton to Einstein and Planck.
Thus basic CW sum-and-difference phase relations seem to underlie the physics of Poincare contact geometry. This in turn is based on circular and hyperbolic geometry described next.
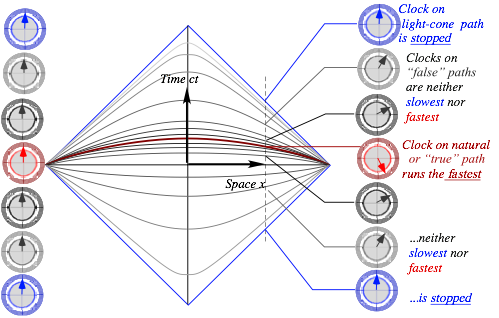
Fig. 5.2 “True” paths carry extreme
phase and fastest clocks. Light-cone has only stopped clocks.

Fig. 5.3 Quantum waves interfere
constructively on “True” path but mostly cancel elsewhere.
Geometry of circular and hyperbolic functions
Geometry of half-sum and half-difference phase P=(R+L)/2 and group G=(R-L)/2 vectors is based on trigonometric exponential identities that are crown jewels of 18th century mathematics and have Euclidian geometric origins shown in Fig. 5.4. Phase angle-ö identities apply to Fig. 5.4a.
![]() (5.11a)
(5.11a) ![]() (5.11b)
(5.11b)
Circular function tanö is named for a tangent to a unit circle shown in Fig. 5.4(a). Its incline (sine) elevation is sinö. The complimentary tangent or cotangent cotö completes the tangent distance between axes where ö is circle arc-length-ö or subtended area-ö. Hyperbolic functions use area Ė for “angle.”
![]() (5.12c)
(5.12c) ![]() (5.12d)
(5.12d)
Fig. 5.4b shows how hyperbolic functions relate to circular ones in Fig. 5.4a. The circular sine equals the hyperbolic tangent (sinö =tanhĖ) and vice versa (tanö =sinhĖ). Each circular function has a segment that matches one for a hyperbolic function, for example (cosö =sechĖ) matches (secö =coshĖ). These relations recap the CW view of the Legendre contact transformation in Fig. 5.1 that underlies classical and quantum theory that is in the algebra and geometry for every bit of light-and-matter in and around us!
In Fig. 5.4, circular area ö and hyperbolic area Ė have been chosen so that tanö =1.15=sinhĖ and sinö =0.75=tanhĖ, that is for u=3c/4. The tangent to the circle in Fig. 5.4a-b is like the one that contacts the Lagrangian circle in Fig. 5.1b to contact-transform it to the Hamiltonian hyperbola in Fig. 5.1a, and vice versa the hyperbolic tangent in Fig. 5.4b is like the one that transforms the Hamiltonian hyperbola in Fig. 5.1a to the Lagrangian circle in Fig. 5.1b.
The
hyperbolic tangent u/c=tanhĖ
of (2.19) corresponds to frame rapidity Ė and group velocity u=Vgroup![]() in (2.8), (4.9) and in Fig. 3.3a-b. The
circular tangent angle ö or inclination sinö belongs to Lagrangian velocity function
(5.10) in Fig. 5.1b. (The horizontal axis of the latter in the vertical axis of
Fig.11. This geometry is symmetric to axis-switching.) As u and Ė approach c and į, respectively, the circular
angle ö
approaches ð/2.
in (2.8), (4.9) and in Fig. 3.3a-b. The
circular tangent angle ö or inclination sinö belongs to Lagrangian velocity function
(5.10) in Fig. 5.1b. (The horizontal axis of the latter in the vertical axis of
Fig.11. This geometry is symmetric to axis-switching.) As u and Ė approach c and į, respectively, the circular
angle ö
approaches ð/2.
This angle ö is the stellar velocity aberration angle, that is, the polar angle that vertical starlight is seen by a horizontally moving astronomer to tip into her direction of motion. Aberration angle ö, like rapidity Ė, is 1st-order in velocity u and both Ė and ö equal u/c at low speeds. (See the discussion of Fig. 5.6 near the end of this chapter. This deepens the development to include 4-vector space-time.)
Many of the twelve circular-hyperbolic trigonometric ratios in Fig. 5.1 belong to one or more physical or geometric effects shown in prior diagrams beginning with Euclid’s rectangle-in-circle mean construction of Fig. 3.3. Prior ratio constructions are overlapped in the form of Fig. 5.1 and results in Fig. 5.5a that might be described as a global ratio riot. This riot is simplified and labeled in zoom-in views of Fig. 5.5b-d and they are the basis of the following discussion of the role of tangent-contact geometry in CW analysis of Poincare contact transformation and relativistic quantum waves.
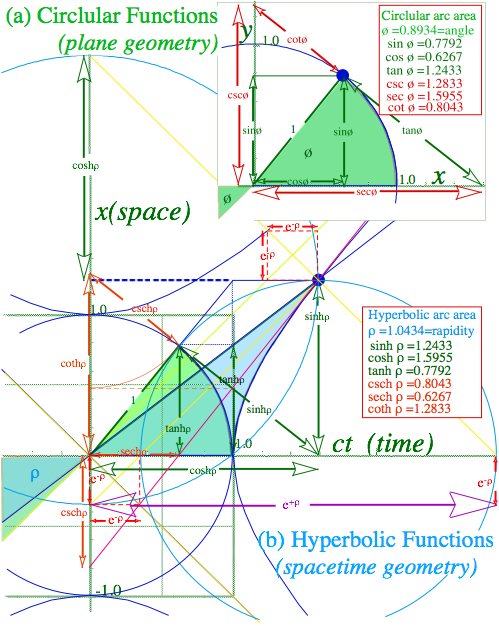
Fig. 5.4 Trigonometric geometry (a)
Unit circular area ö=0.86
and (b) Unit hyperbolic area Ė=0.99.
Beginning with the Euclidian mean diagram of Fig. 3.3, three mean frequencies arise from an interfering pair of left-moving “red” and right-moving “blue” beams of frequency ĚL and ĚR. First is a half-sum phase frequency Ěp=(ĚR+ĚL)/2 (arithmetic mean) that defines the circle radius in Fig. 3.3. Second is a half-difference group beat frequency Ěg=(ĚR-ĚL)/2 (difference mean) that is radial distance of circle center to origin. Third is a root-product proper frequency ϖ =( ĚRŠĚL)1/2 (geometric mean) that is the base radius or bottom of a Ě(k) hyperbola of rest energy B=h ϖ =Mc2 above origin in Fig. 3.3.
Phase and group frequencies are defined as ratios or shifts of the geometric mean frequency ϖ, and this begins with the Doppler shift definition of the red ĚL=e−Ėϖ and blue ĚR=e+Ėϖ CW components. Ratio values Ěp=ϖcoshĖ and Ěg=ϖsinhĖ define each point on a ϖ-hyperbola dispersion curve in Fig. 5.5.
Fig. 5.5 is based on circles with three different radii, one for each mean frequency. The base circle-b drawn centered at origin has radius B=h ϖ =Mc2 of the Lagrangian circle in Fig. 5.1b. A smaller circle-g has group radius hĚg=BsinhĖ. A larger circle-p has phase radius hĚp=BcoshĖ of the Euclidean circle in Fig. 3.3 and is drawn with dashed lines in Fig. 5.5. (Base value B is scaled for energy here.)
Circle-p of larger radius hĚp=BcoshĖ is centered at cp=hĚg=BsinhĖ, a horizontal distance equal to the radius of the smaller circle-g, while the latter is centered at E=hĚp=BcoshĖ, a vertical distance equal to the radius of the larger circle-p. Tangents that contact circles or hyperbolas define many of the physical quantities labeled in the zoom-in view of Fig. 5.5b. Intersections and chords shared by two of the circles also provide the key quantities as seen in Fig. 5.5a.
So far the CW development has emphasized the Doppler ratio as a starting point beginning with Fig. 2.2 and culminating with the Euclidean means of Fig. 3.3. However, most developments of relativity start with velocity u, and that geometric approach is excerpted in a simplified construction of Fig. 5.5c where u/c=45/53 and Fig. 5.5d where u/c=3/5. (Fig. 5.5a-b and most other figures use u/c=3/5.) Once the velocity u/c line intersects the basic b-circle and its horizontal tangent of unit-energy (B=1=Mc2), it only takes three more lines to derive Lagrangian -L=BsechĖ, then momentum cp=BsinhĖ, and finally the Hamiltonian H=BcoshĖ. Then a compass is used to check accuracy with the phase p-circle by making sure it goes from (cp,H) to the (0,B)-point on top of the b-circle. The p-circle goes on to intersect the negative cp-axis at the Doppler red shift rB=Be+Ė. Finally, the group g-circle in Fig. 5.5a-b has a chord intersection with the p-circle that is the hyperbolic contact tangent, and it grazes the ö-angle normal to the Lagrangian circle tangent in Fig. 5.5b. This helps to clarify geometry of H-L contact transformations of Fig. 5.1 for reciprocal space-time (Ě,ck) and (Ö,u/c). The constructions also apply to space-time.
If
Fig. 5.5 is in space-time, the segment -L=BsechĖ is Lorentz contraction ![]() .
The H=BcoshĖ and cp=BsinhĖ segments are,
respectively Einstien time dilation
.
The H=BcoshĖ and cp=BsinhĖ segments are,
respectively Einstien time dilation ![]() and asimultaneity a=ud/c
coefficients. Node-to-node or peak-to-peak gaps contract by l= in Fig. 2.2d-e. As speed reduces in Fig. 5.5c-d from u/c=45/53 to u/c=3/5 or to lower values, the
Lagrangian velocity angle ö and Hamiltonian rapidity Ė
approach the velocity ratio u/c.
Galilean velocity addition rules resume. In the opposite ultra-relativistic
regime, ö approaches ð/2, Ė approaches į, and u/c nears unit slope or 45° in Fig. 5.5c. But,
Galilean-like rules (3.6) apply to rapidity Ė at all speeds (so far).
and asimultaneity a=ud/c
coefficients. Node-to-node or peak-to-peak gaps contract by l= in Fig. 2.2d-e. As speed reduces in Fig. 5.5c-d from u/c=45/53 to u/c=3/5 or to lower values, the
Lagrangian velocity angle ö and Hamiltonian rapidity Ė
approach the velocity ratio u/c.
Galilean velocity addition rules resume. In the opposite ultra-relativistic
regime, ö approaches ð/2, Ė approaches į, and u/c nears unit slope or 45° in Fig. 5.5c. But,
Galilean-like rules (3.6) apply to rapidity Ė at all speeds (so far).
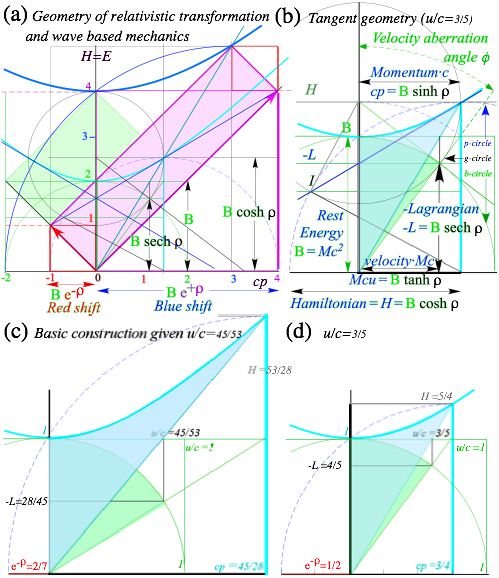
Fig. 5.5 Relativistic wave mechanics geometry.
(a) Overview. (b-d) Details of contacting tangents.
Transverse vs. longitudinal Doppler: Stellar aberration
A novel description of relativity by L. C. Epstein[xv] in Relativity Visualized introduces a "cosmic speedometer" consisting of a telescope tube tipped to catch falling light pulses from a distant overhead star. A stationary telescope points straight up the x-axis at the apparent position S of the star. (Fig. 5.6a) But, with velocity u=uzez across to the star beam x-axis, the telescope has to tip to catch the starlight, so the apparent position S' tips toward u. (Fig. 5.6b).
The telescope tips by a stellar aberration angle ó(ö in (5.11a) or Fig. 5.4a.). The sine of angle ó is velocity ratio Č= uz /c which is the hyper-tangent of relativistic rapidity õz (Ė in (5.12a) or Fig. 5.4b.)
Č= uz /c =sin ó = tanh õz (5.13)
Proper
time ô and frequency ![]() invariance (3.10) forces 4-vector components normal to velocity u
of a boost to be unchanged. That is, a boost along z of (ct,z)
to (ct',z')
(or (Ě,ckz)
to (Ě',ckz')
) must preserve both (x,y)=(x',y')
and (ckx,cky)=(ckx',cky')
just as a rotation in the xy-plane of (x,y)
to (x',y')
leaves unaffected the components (ct,z)=(ct',z')
and (Ě,ckz)=(Ě',ckz')
transverse to the rotation.
invariance (3.10) forces 4-vector components normal to velocity u
of a boost to be unchanged. That is, a boost along z of (ct,z)
to (ct',z')
(or (Ě,ckz)
to (Ě',ckz')
) must preserve both (x,y)=(x',y')
and (ckx,cky)=(ckx',cky')
just as a rotation in the xy-plane of (x,y)
to (x',y')
leaves unaffected the components (ct,z)=(ct',z')
and (Ě,ckz)=(Ě',ckz')
transverse to the rotation.
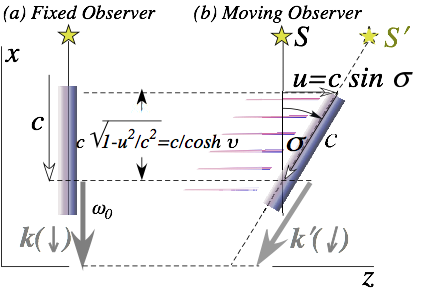
Fig. 5.6 Epstein’s cosmic
speedometer with aberration angle ó and transverse Doppler shift coshõ.
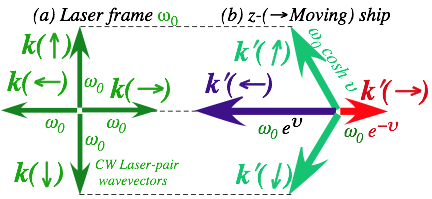
Fig. 5.7 CW version of cosmic speedometer showing transverse and longitudinal k-vectors.
Invariant (3.10) demands light-speed conservation as sketched in Fig. 5.6b. Starlight speed down the ó-tipped telescope is c, so the x-component of starlight velocity reduces from c to
cx'=c cos ó=c√(1- uz2/c2) = c/cosh õz . (5.14)
Transformation (5.17a) below assures that x-or-y-components of k↓ are unchanged by uz-boost.
(ckx,cky)=(ckx',cky') (5.15)
So the length of k↓ increases by a factor cosh õ as shown in Fig. 5.7 as does the frequency Ě'↓.
c|k′↓| = c|k↓| coshõz = Ě0 cosh õz =Ě0/√(1-u2/c2) (5.16)
If the observer crosses a star ray at very large velocity, that is, lets uz approach c, then the star angle ó approaches 90° and the frequency increases until the observer sees an X-ray or č-ray star coming almost head on! The coshõz factor is a transverse Doppler shift. For large õz, it approaches eõz, which is the ordinary longitudinal Doppler shift upon which the CW relativity derivations of Ch. 2 are based. Relations (5.13-16) are summarized in a 4-vector transformation: Ě0 has a transverse Doppler shift to Ě0coshõz, so ckz=0 becomes ckz' = -Ě0 sinhõz , but the x-component is unchanged: ckx' = Ě0 = ckx.
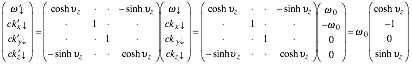
(5.17a)
If starlight had been k← or k→ waves going along u and z-axis, the usual longitudinal Doppler blue shifts e+õz or red shifts e−õz would appear on both the k-vector and the frequency, as stated by the following.
 (5.17b)
(5.17b)
The Epstein speedometer tracks light pulses and particles in space and time. Instead of space-x and time-ct coordinates of a Minkowski graph, he plots space coordinate-x against proper time-cô. This view has all things, light č and particle P included, moving at the speed of light as shown in Fig. 5.8. Light never ages, so its “speedometer” is tipped to the maximum along x-axis.

Fig. 5.8 Space-proper-time plot makes all objects move at speed c along their cosmic speedometer.
One cute feature of the Epstein space-proper-time view is its take of the Lorentz-Fitzgerald contraction of a proper length L to L′=L√1-u2/c2. (Recall discussion around (2.11).) As shown in Fig. 5.9 below, L′ is simply the projection onto the x-axis of a length L tipped by ó.
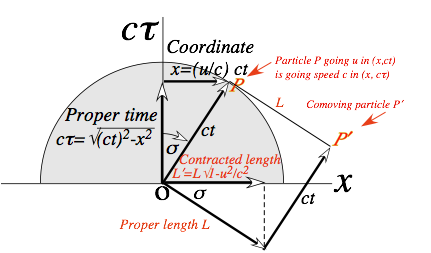
Fig. 5.9 Space-proper-time plot of Lorentz contraction as geometric projection of rotated line L.
The problem with the (x,cô) view is that a space-time event is not plotted as a single point for all observers. Since the time parameter ô is an invariant, the (x,cô) graph it is not a metric space.
Graphical wave 4-vector transformation
Geometric constructions combining Fig. 5.6 and Fig. 5.7 help to quantitatively visualize 4-wavevector transformations. One is shown in Fig. 5.10. The c-dial of the “speedometer” is first set to the desired u-speed which determines angle ó. The top of the c-dial (which may also represent a transverse ck↑-vector in units of Lab frequency Ě0) is projected parallel to the velocity axis until it intersects the c-dial vertical axis. A transformed ck'↑-vector of length Ě'↑=Ě0 cosh õ results, similar to ck'↓ in (5.17a). Both ck'↑ and ck'↓ have a projection on the velocity axis of Ě0sinh õ while maintaining their transverse components Ě0 and -Ě0 , respectively, in order to stay on the light cone.
A dashed circle of radius cosh õ is drawn concentric to the c-dial and determines the longitudinal vectors ck'→ and ck'← of Doppler shifted length and frequency Ě0e-õ and Ě0eõ, respectively, as required by transformation (5.17b). This construction is part of Fig. 5.4 and Fig. 5.5.
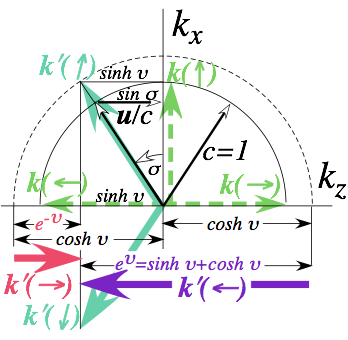
Fig. 5.10 CW cosmic speedometer.
Geometry of Lorentz boost of counter-propagating waves.
Symmetry and conservation principles
In Newtonian theory the first law or axiom is momentum conservation. Physical axioms, by definition, have only experimental proof. Logical proof is impossible unless a theory like Newton’s becomes sub-summed by a more general theory with finer axioms. Proof of an axiom then undermines it so it becomes a theorem or result of more basic axioms. (Or else an axiom might be disproved or reduced to an approximate result subject to certain conditions.)
The logic of axioms yielding results or theorems in mathematical science probably goes back two thousand years to the time of Euclid’s Elements. Also, axiomatic approaches to philosophy and natural science show up in writings as early as that of Occam or even Aristotle, but it is not until the European Renaissance that experiments began to be precise enough to support mathematical models. By the European Enlightenment period, mathematical logic of physical science had become more effective and productive than any preceding philosophy due in no small part to increasingly precise evidence.
As stated by introduction, current time and frequency measurements have achieved almost unimaginable precision. In celebration of this, two continuous wave (CW) axioms (1.1-2) have been used to undermine Newtonian axioms for mass, energy, and momentum. They then became approximate results (4.4) and give rise to exact equivalents of Newtonian concepts in Einstein and Planck relativity and quantum theory in (4.5). It is a non-trivial example of undermining axioms by Occam razor-cutting.
The undermining of Newton’s first axiom (momentum conservation) by the shaved CW axioms is a good example to expose the logic involved. CW logic leads to the DeBroglie scaling law (4.5b) that equates momentum p to wavevector k scaled in h units. A rough statement of how CW axioms undermine or “prove” p-conservation axioms is that k-conservation is required by wave coherence and so p=hk must be conserved, as well. However, that oversimplifies a deeper nature of what is really symmetry logic.
A
strength (and also, weakness) of CW axioms (1.1-2) is that they are symmetry
principles due to the Lorentz-Poincare isotropy of space-time that invokes
invariance to translation ![]() in the vacuum. Operator
in the vacuum. Operator ![]() has
plane wave eigenfunctions
has
plane wave eigenfunctions ![]() with roots-of-unity eigenvalues
with roots-of-unity eigenvalues ![]() .
.
![]() (5.18a)
(5.18a) ![]() (5.18b)
(5.18b)
This also applies to 2-part or “2-particle” states ![]() where exponents add (k,Ě)-values of each constituent to K=k1+k2 and
Ű=Ě1+Ě2, and
where exponents add (k,Ě)-values of each constituent to K=k1+k2 and
Ű=Ě1+Ě2, and ![]() -eigenvalues
also have the form
-eigenvalues
also have the form ![]() of
(5.1). Matrix
of
(5.1). Matrix ![]() of T-symmetric evolution U is zero unless
of T-symmetric evolution U is zero unless ![]() and
and ![]() .
.
T-symmetry
requires total energy ![]() and total momentum
and total momentum ![]() be conserved for archetypical CW
states, but laboratory CW have momentum uncertainty Äk=1/Äx due to finite beam size
be conserved for archetypical CW
states, but laboratory CW have momentum uncertainty Äk=1/Äx due to finite beam size![]() and
energy uncertainty due to time limits. So, Newton’s 1st law or axiom
is verified but only as an ideal limit.
and
energy uncertainty due to time limits. So, Newton’s 1st law or axiom
is verified but only as an ideal limit.
Symmetry is to physics what religion is to politics. Both are deep and grand in principle but roundly flaunted in practice. Both gain power quickly by overlooking details. In Ch.4 relativistic and quantum kinetic properties of a massive “thing” arise from those of an optical 2-CW function in one space dimension. This means that mass shares symmetry with 2-CW light, not that mass is 2-CW light. Massive “things” do not vanish if a laser turns off, but our tiny optical mass hNĚ/c2 is quickly gone!
Puzzling questions remain. Why do simple wave optics lead directly to general properties (4.5) of relativity and quantum mechanics of a massive particle? How does a cavity of counter-propagating green light waves act like it holds particles of mass M=hĚ/c2?
A
short answer to one question is that particles are waves, too, and so forced by
Lorentz symmetry to use available hyperbolic invariants ![]() for dispersion. To answer the second
question entails further loss of classical innocence. In Ch. 6 Occam’s razor is
again applied to cut semi-classical CW laser fields down to single field quanta
for dispersion. To answer the second
question entails further loss of classical innocence. In Ch. 6 Occam’s razor is
again applied to cut semi-classical CW laser fields down to single field quanta
![]() or
photons. So the second short
answer is that waves are particles, too, even for optical dispersion
or
photons. So the second short
answer is that waves are particles, too, even for optical dispersion ![]() .
.
By many accounts, quantum theory begins with Planck axiom E=hNĚ. This is distinguished from the scaling law E=sĚ derived in (4.5a) since its scale factor s=hN is not an obvious consequence of CW phase axioms (1.1-2) that lead to (4.5). CW logic involves additional axioms for Maxwell electromagnetic energy E and field amplitude quantization to render Planck’s axiom. This is discussed shortly.
1st
and 2nd Quantization: phase vs. amplitude
Waves
resonate at discrete wave numbers ![]() in a ring or cavity of length L.
Then relations (4.5b) between k and momentum
p force p-quantization
in a ring or cavity of length L.
Then relations (4.5b) between k and momentum
p force p-quantization
![]() so momentum quantum numbers[xvi] m=0, Ī1, Ī2,… count waves on ring L
as in Bohr electron orbitals or for cavity modes in (4.6a).
so momentum quantum numbers[xvi] m=0, Ī1, Ī2,… count waves on ring L
as in Bohr electron orbitals or for cavity modes in (4.6a).
Then Planck
dispersion ![]() (4.5a)
gives electron energy levels
(4.5a)
gives electron energy levels ![]() for
the BS approximation
for
the BS approximation ![]() or for cavity fundamental frequency
levels (4.6b). Wave-fitting in x-space
is called 1st
quantization. Related fitting in wave amplitude space is called 2nd quantization.
or for cavity fundamental frequency
levels (4.6b). Wave-fitting in x-space
is called 1st
quantization. Related fitting in wave amplitude space is called 2nd quantization.
Heisenberg[xvii] showed quanta ![]() or
or![]() arise from eigenvalues (literally
“own-values”) of matrix operators
arise from eigenvalues (literally
“own-values”) of matrix operators ![]() or
or
![]() whose eigenvectors (“own-vectors”)
whose eigenvectors (“own-vectors”) ![]() or
or
![]() may be superimposed.
may be superimposed.
![]() … (5.20)
… (5.20)
(Dirac’s bra-ket[xviii] notation came later.) Allowing things to be
at (or in) m places (or states) allows mean
values ![]() to range continuously from lowest quantum
levels
to range continuously from lowest quantum
levels ![]() to the highest
to the highest ![]() .
.
![]() … (5.21)
… (5.21)
For classicists, the
notion that each multiple-personality-k has a probability![]() seems,
if not crazy, then at least dicey in the sense of Einstein’s skeptical quote, “God
does not play dice…” [xix]
seems,
if not crazy, then at least dicey in the sense of Einstein’s skeptical quote, “God
does not play dice…” [xix]
But, superposition is an idea borrowed from classical waves. Resulting interference makes them ultra-sensitive to relative position and velocity, a first order sensitivity that leads elegantly to relativity transformation (2.10) and kinematic relations (4.5) by geometry of optical phase kx-Ět of Ņ=Aei(kx-Ět).
Amplitude “A” of wave (1.6) or (1.9) is set arbitrarily since only real wave zeros were needed. It is ignored in (5.5). Without Maxwell and Planck rules, CW amplitude or wave quantity is undefined and un-quantized while wave quality (frequency and phase) may be well defined and quantized. Amplitudes need a similar treatment that is begun in Ch. 6.
Chapter 6. Variation and quantization of optical amplitudes
What is deduced from wave phase alone? Wave amplitude has so far been skirted for Occam economy: “Pluralitas non est ponenda sine neccesitate” (Assume no plurality without necessity.) CW phase axioms (1.1-2) give Lorentz-Doppler and Planck-DeBroglie symmetry relations yet 2-CW amplitudes (1.10) are not defined beyond assuming their 1-CW amplitudes match. Standing wave grid reference frames in Fig. 2.1 and Fig. 2.2 are just points where amplitude is zero, that is, loci of real wave function roots.
Discussion
of non-zero amplitude variation begins with counter-propagating 2-CW dynamics
involving two 1-CW amplitudes ![]() and
and ![]() that we now allow to be unmatched.
that we now allow to be unmatched. ![]()
![]() (6.1a)
(6.1a)
Half-sum mean phase
rates ![]() and
half-difference means
and
half-difference means ![]() appear
here as in (1.10).
appear
here as in (1.10).
![]() (6.1b)
(6.1b) ![]() (6.1c)
(6.1c)
Also important is
amplitude mean ![]() and half-difference
and half-difference![]() .
Wave motion depends on standing-wave-ratio SWR
or the inverse standing-wave-quotient SWQ.
.
Wave motion depends on standing-wave-ratio SWR
or the inverse standing-wave-quotient SWQ.
![]() (6.2a)
(6.2a) ![]() (6.2a)
(6.2a)
Recall mean frequency ratios for group velocity (2.3b) or its inverse that is phase velocity (2.3a).
![]() (6.3a)
(6.3a) ![]() (6.3b)
(6.3b)
A 2-state amplitude
continuum is bounded by a pure right-moving 1-CW ![]() of SWR=1 and a pure left-moving
1-CW
of SWR=1 and a pure left-moving
1-CW ![]() of
SWR=-1. A 2-CW standing-wave
of
SWR=-1. A 2-CW standing-wave ![]() has SWR=0.
has SWR=0.
Wave paths for various SWR values are drawn in Fig. 6.1 for 600THz 2-CW pairs and in Fig. 6.2 for Doppler shifted 300THz and 1200THz 2-CW pairs at the same SWR values. The SWQ is the ratio of the envelope peak (interference maximum) to the envelope valley (interference minimum), and vice versa for SWR=1/SWQ. Single frequency 2-CW paths of nonzero-SWR in Fig. 6.1 do a galloping motion. Each wave speeds up to peak speed c/SWR=cŠSWQ as it first shrinks to squeeze through its envelope minima and then slows to resting speed cŠSWR as it expands to its maximum amplitude. Only at zero-SWR do 2-CW zero-paths appear to travel at a constant group speed (6.3a) and phase speed (6.3b) as in Fig. 6.1c or 6.2c. (For 1-CW paths or unit SWR=Ī1 there is just one speed Īc by axiom (1.1).)
The real and imaginary parts take turns. One gallops while the other rests and vice versa and this occurs twice each optical period. If frequency ratio (6.3) and amplitude ratio (6.2) have opposite signs as in Fig. 6.1c (Ī0 or Īį) and in Fig. 6.2e (Ī3/5 or Ī5/3), wave zero paths will follow a right angle staircase. 1-frequency staircase (Vgroup=0=SWR) in Fig. 6.1c is a Cartesian grid like Fig. 2.1c. 2-frequency waves (Vgroup≠0) have Minkowski grids like Fig. 2.2c for SWR=0 or quasi-Cartesian stair steps like Fig. 6.2e for Vgroup=-cSWR. To broadcast Cartesian grids to a u-frame one tunes both Vgroup and cSWR to u.
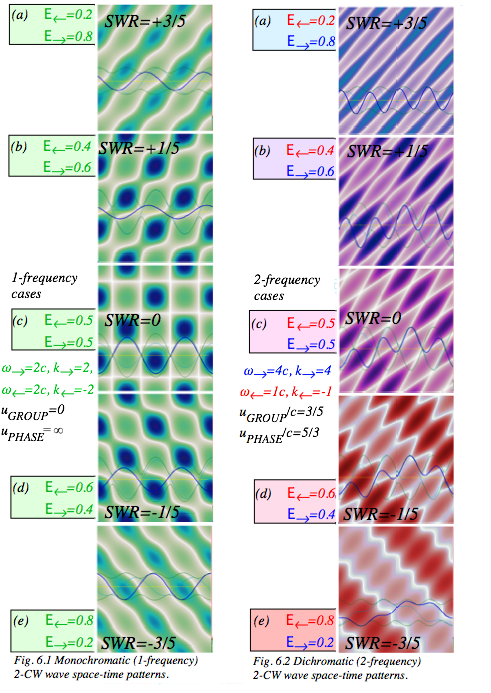
Galloping is a fundamental interference property that may be clarified by analogy with elliptic orbits of isotropic 2D-harmonic oscillators and in particular with elliptic polarization of optical wave amplitudes. Fig. 6.3 relates polarization states and wave states of Fig. 6.1 beginning with left (right)-circular polarization that is analogous to a left (right)-moving wave in Fig. 6.3g (Fig. 6.3a). As sketched in Fig. 6.3(b-e), galloping waves are general cases analogous to general states of elliptic polarization or general 2DHO orbits obeying a Keplerian geometry shown in Fig. 6.3h. Standing waves correspond to plane-polarization. Polarization in the x-plane of Fig. 6.3d corresponds to a standing cosine wave and y-plane polarization (not shown) would correspond to a standing sine wave.
Isotropic oscillator orbits obey Kepler’s law of constant orbital momentum. Orbit angular velocity slows down by a factor b/a at major axes or aphelions Īa and then speeds up by a factor a/b at minor axes or perihelions Īb just as a galloping wave, twice in each period, slows down to SWRŠc and speeds up to SWQŠc. The galloping or eccentric motion of the eccentric anomaly angle ö(t) in Fig. 6.3h is a projection of a uniformly rotating mean anomaly (phase angle ĚŠt) of the isotropic oscillator, and this gives a Keplarian relation of the two angles seen in the figure.
![]() (6.4a)
(6.4a)
The eccentric anomaly time derivative of ö (angular velocity) gallops between Ě Šb/a and Ě Ša/b.
![]() (6.4b)
(6.4b)
The product of
angular moment r2 and ![]() is
orbital momentum, a constant proportional to ellipse area.
is
orbital momentum, a constant proportional to ellipse area.
![]()
Consider galloping wave zeros of a monochromatic wave (6.1a) having SWQ (6.2b).
Space k0x varies with time Ě0t in the same way that eccentric anomaly varies in (6.4a).
![]() (6.5a)
(6.5a)
Speed of galloping wave zeros is the time derivative of root location x in units of light velocity c.
![]() (6.5b)
(6.5b)
Single frequency 2-CW paths in Fig. 6.1 have a constant product of instantaneous wave velocity and wave amplitude analogous to the constant product of orbital velocity and radius. So vacuum optical amplitude and phase motion obey a funny version of Kepler and Galileo’s rules. The extent to which 14th century geometric relations underlie basic wave physics has not been fully appreciated.
Classical Maxwell
field amplitudes![]() and
and![]() are derivatives of vector potential A.
Maxwell energy
U per volume V
or total energy UŠV
is a sum of amplitude squares E•E and c2B•B.
are derivatives of vector potential A.
Maxwell energy
U per volume V
or total energy UŠV
is a sum of amplitude squares E•E and c2B•B.
Fourier analysis of A
into amplitudes ![]() and
and
![]() leads
to a harmonic oscillator sum over each plane CW mode frequency
leads
to a harmonic oscillator sum over each plane CW mode frequency![]() ,
km-vector allowed by a
large-cavity, and polarization á=x,y
normal to km.
,
km-vector allowed by a
large-cavity, and polarization á=x,y
normal to km.
![]() (6.8)
(6.8)
Harmonic oscillator frequency is independent of amplitude. This is consistent with CW phase axiom (1.1) and dispersion relations (3.5) derived from 2-CW superposition, but such a simple axiom seems unable to derive the Maxwell vector amplitude structure of 2-dimensional polarization normal to km of each wave mode or even to establish that its wave variables A, B, E, or km are, in fact, 3D vectors.
The CW axiom (1.1) gives what is effectively a 2-dimensional harmonic oscillator (2DHO) with two complex amplitudes (aL, aR) for the two longitudinal propagation directions, but each comes with two transverse polarization amplitudes (ax, ay) that describe the second 2DHO in Maxwell light, namely polarization ellipsometry used in Fig. 6.3 as an analogy for propagation left-and-right along z.
Mode amplitude![]() or
or
![]() in classical electromagnetic energy
in classical electromagnetic energy![]() are
replaced by oscillator operators
are
replaced by oscillator operators ![]() or
or
![]() for
a field Hamiltonian with explicit linear frequency dependence of Planck.
for
a field Hamiltonian with explicit linear frequency dependence of Planck.
The H-eigenstates ![]() for
exactly quantized photon numbers
for
exactly quantized photon numbers ![]() fix a definite energy value
fix a definite energy value ![]() for
each mode-km but has quite uncertain field phase. Average energy of one mode is
for
each mode-km but has quite uncertain field phase. Average energy of one mode is
![]() (6.10a)
(6.10a)
where a 1-CW-1-photon E-field and vector potential A-amplitude is as follows.
![]() (6.10b)
(6.10b) ![]() (6.10c)
(6.10c)
Field
quantization is called 2nd-quantization to distinguish 1st-quantization
km mode
numbers m, used for classical light,
from “purely quantum” photon
numbers ![]() for
wave amplitude. This may be a prejudice that waves (particles) are usual
(unusual) for light but unusual (usual) for matter. Amplitudes
involve relations (6.7) to (6.10) that are more complex than axioms (1.1-2) for
wave phase. While Maxwell-Planck relations lack the simplicity of the latter,
they do derive the linear dispersion (1.1) by Fourier transform of the Maxwell
wave equations, and they show optical wave amplitude has an internal symmetry
analogous to that of wave frequency. The following discussion of this analogy
involves a Doppler shift of wave amplitude
with invariance or covariance of photon number Nk
and standing wave ratio (SWR)
(6.5). Also, one begins to see how Born quantum probability formulas
for
wave amplitude. This may be a prejudice that waves (particles) are usual
(unusual) for light but unusual (usual) for matter. Amplitudes
involve relations (6.7) to (6.10) that are more complex than axioms (1.1-2) for
wave phase. While Maxwell-Planck relations lack the simplicity of the latter,
they do derive the linear dispersion (1.1) by Fourier transform of the Maxwell
wave equations, and they show optical wave amplitude has an internal symmetry
analogous to that of wave frequency. The following discussion of this analogy
involves a Doppler shift of wave amplitude
with invariance or covariance of photon number Nk
and standing wave ratio (SWR)
(6.5). Also, one begins to see how Born quantum probability formulas ![]() arise and are consistent with Dirac
amplitude covariance.
arise and are consistent with Dirac
amplitude covariance.
Relativistic 1-CW covariance of Poynting flux
Maxwell-Planck energy density U(Joule/m3) in (6.10a) leads to a related Poynting flux S[Joule/(m2Šs)].
![]() where:
where: ![]() (6.11)
(6.11)
Flux S contains two frequency factors, the fundamental laser frequency Ěk and the photon count rate nk per[ (m2Šs)]. Frequency Ěk is quantum quality of a laser beam and rate nk is its quantum quantity. The product hĚkŠnk is Poynting flux. Rate nk and frequency Ěk both Doppler shift by an exponential eĪĖ of rapidity Ė in (2.16). So do 1-CW fields EĪk as may be shown by Lorentz transforming them directly.
![]() (6.12a)
(6.12a) ![]() (6.12b)
(6.12b)
Thus both electric field polarization E-amplitudes Ex an Ey of a 1-CW field undergo the same eĪĖ Doppler shift that the frequency Ěk or wavevector k experience. If E in (6.11) scaled by 1-photon factor (6.10) a probability wave Ņ follows whose square Ņ∗Ņ is a volume photon count N/(m3).
Or, a flux probability wave Ņ is defined so its square Ņ∗Ņ is an expected flux photon count n/(m2Šs).
![]() (6.13b)
(6.13b)
Due to the ![]() scaling
of (6.13) the Doppler factor of
scaling
of (6.13) the Doppler factor of ![]() drops
an eĪĖ/2 factor
from Ek
in (6.12).
drops
an eĪĖ/2 factor
from Ek
in (6.12).
This is a starting point for the spinor form of Lorentz transformation for Dirac amplitudes.
Relativistic 2-CW invariance of cavity quanta
Mean photon number![]() of
a 2-CW cavity mode, unlike a 1-CW flux quantum nk, is invariant to
cavity speed. By analogy, 2-CW modes have variant group-phase velocity (Vgroup, Vphase),
energy-momentum (hck,hĚ),
but invariant mean velocity
of
a 2-CW cavity mode, unlike a 1-CW flux quantum nk, is invariant to
cavity speed. By analogy, 2-CW modes have variant group-phase velocity (Vgroup, Vphase),
energy-momentum (hck,hĚ),
but invariant mean velocity ![]() and
frequency
and
frequency![]() .
.
![]() (6.15a)
(6.15a) ![]() (6.15b)
(6.15b)
Linear dispersion ĚĪk=Īck and (1.11) or (2.7) are used. Note the analogy to SWR relations (6.2).
![]() (6.15c)
(6.15c) ![]() (6.15d)
(6.15d)
Each ratio (6.15) is a wave velocity that Doppler-transforms like relativistic (non-Galilean) velocity.
![]() (6.16a)
(6.16a) ![]() (6.16b)
(6.16b)
Velocity uAB/c=tanhĖAB is a hyperbolic sum since rapidity is a simple sum ĖAB= ĖA+ ĖB by (3.6).
![]() (6.17)
(6.17)
The energy and
momentum flux values are found for counter-k
2-CW beam functions ![]() .
.
![]()
Lab 1-CW flux number
expectation values ![]() give 2-CW flux expectations in lab.
give 2-CW flux expectations in lab.
The relation (6.13b)
of quantum field ![]() and classical Maxwell
and classical Maxwell ![]() -field
expectation is used.
-field
expectation is used.
![]() (6.18a)
(6.18a)
![]() (6.18b)
(6.18b)
Values ![]() and
and
![]() lie on an invariant hyperbola of constant
geometric means
lie on an invariant hyperbola of constant
geometric means ![]() or
or
![]() 2.
2.
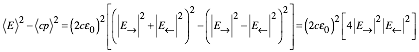
![]() (6.19)
(6.19)
![]() (6.20a)
(6.20a)
The geometric mean
frequency ![]() ,
mean quantum number
,
mean quantum number ![]() ,
and mean field
,
and mean field ![]() are defined.
are defined.
![]() (6.20b)
(6.20b) ![]() (6.20c)
(6.20c) ![]() (6.20d)
(6.20d)
Doppler
relations imply Lorentz invariance for the mean number ![]() and for the mean frequency
and for the mean frequency ![]() as well as their geometric mean
as well as their geometric mean ![]() that
is 2cĆ0
times the mean field
that
is 2cĆ0
times the mean field![]() and
applies to a general 2-CW beam function Į.
A factor 2 on
and
applies to a general 2-CW beam function Į.
A factor 2 on ![]() or
or ![]() in (6.20a) is consistent with 1-photon
2-CW states having equal average number
in (6.20a) is consistent with 1-photon
2-CW states having equal average number ![]() and
total1-photon Planck energy expectation E=hĚ.
and
total1-photon Planck energy expectation E=hĚ.
Ideal
cavities balance field ![]() ,
frequency
,
frequency ![]() ,
and number. But, a general beam with
,
and number. But, a general beam with ![]() ,
,
![]() ,
and
,
and ![]() has a center-of-momentum CoM-frame of zero flux where
has a center-of-momentum CoM-frame of zero flux where ![]() by (6.18b), an isochromatic IsoC-frame with
by (6.18b), an isochromatic IsoC-frame with ![]() ,
and an IsoN-frame
with balanced photon count
,
and an IsoN-frame
with balanced photon count![]() .
Frame speeds uá may be
distinct as sketched in Fig. 6.4.
.
Frame speeds uá may be
distinct as sketched in Fig. 6.4.
![]() (6.21a)
(6.21a) ![]() (6.21b)
(6.21b) ![]() (6.21c)
(6.21c)
Flux invariant ![]() is maximized by balanced amplitude
is maximized by balanced amplitude ![]() but
is zero if
but
is zero if ![]() or
or ![]() is zero.
is zero.
Thus optical rest mass (6.20a) decreases continuously as a 2-CW beam is unbalanced toward 1-CW.
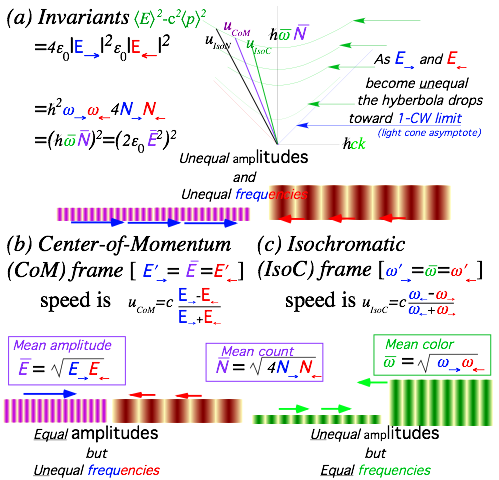
Fig.
6.4. Cavity 2-CW modes. (a) Invariant “mass” hyperbolas. (b) COM frame. (c)
ISOC frame.
It is argued in Ch. 4
that mass is a coherent 2-CW interference effect that is not possible for a 1-CW beam. If we replace Planck energy relation ![]() by a Maslov form
by a Maslov form ![]() it
has a tiny zero-point energy minimum
it
has a tiny zero-point energy minimum![]() .
Does a tiny mass
.
Does a tiny mass![]() exist for 1-CW and even 0-CW beams in all
frames in spite of the incoherence of such zero-point fluctuations? Such a
presence in (6.20) may be ruled out if the speed-of-light axiom (1.1) is exact.
There may still be much to learn about zero-point effects in QED and cosmology
but this seems to indicate that their direct effects are effectively
non-existent.
exist for 1-CW and even 0-CW beams in all
frames in spite of the incoherence of such zero-point fluctuations? Such a
presence in (6.20) may be ruled out if the speed-of-light axiom (1.1) is exact.
There may still be much to learn about zero-point effects in QED and cosmology
but this seems to indicate that their direct effects are effectively
non-existent.
Optical fields A
or E have quantum expectation values of field operators
based on mode amplitudes ![]() or
or
![]() in classical energy
in classical energy![]() .
Each
.
Each![]() or
or
![]() is replaced by oscillator boson operator
is replaced by oscillator boson operator ![]() or
or
![]() in
a quantum field Hamiltonian
in
a quantum field Hamiltonian ![]() whose
eigenstates
whose
eigenstates ![]() have
exact quantized photon numbers
have
exact quantized photon numbers![]() for each mode-km.
for each mode-km.
Each
mode phase quanta m and amplitude quanta Nm
are invariant constants that define another hyperbola with Einstein-Planck
proper frequency![]() as sketched in Fig. 6.4a and Fig. 4.2.
The problem is that absolute certainty of photon number Nm
implies totally uncertain
field phase just as absolutely certain km of 1-CW symmetry implies
totally uncertain
position in space and time.
as sketched in Fig. 6.4a and Fig. 4.2.
The problem is that absolute certainty of photon number Nm
implies totally uncertain
field phase just as absolutely certain km of 1-CW symmetry implies
totally uncertain
position in space and time.
Space-time position coordinates were defined by taking 1-CW combinations to make 2-CW coordinates of Fig. 2.1c or Fig. 2.2c. Ultimately an n-CW pulse-wave (PW) of Fig. 2.1d or Fig. 2.2d was localized with as low a space-time uncertainty Äô as desired but it acquires per-space uncertainty or bandwidth Äõ according to Fourier-Heisenberg relation Äõ Š Äô >1.
So also must photon-number states be combined if amplitude and phase uncertainty are to be reduced to the point where wave space-time coordinates can emerge. Such combinations are known as coherent states or á-states of harmonic oscillation. Sharper wave zeros require fuzzier hyperbolas.
Fuzzy hyperbolas vs. fuzzy coordinates
Model
micro-laser states are coherent
states![]() made
of single-mode eigenstates
made
of single-mode eigenstates ![]() with
amplitudes
with
amplitudes ![]() .
Variable
.
Variable ![]() is average mode phase, and
is average mode phase, and ![]() ,
rescaled by a quantum field factor f, are
field averages
,
rescaled by a quantum field factor f, are
field averages ![]() .
.
![]() (6.22)
(6.22)
Amplitude factor f makes Planck’s ![]() equal Maxwell field energy
equal Maxwell field energy ![]() .
.
![]() (6.23)
(6.23)
A
fundamental laser mode in a 0.25ďm cubic cavity (See E-wave
sketched in a strip of Fig. 2.2c.) has green light with ![]() or 2.5eV per photon. The average
photon number
or 2.5eV per photon. The average
photon number ![]() models a laser with mean energy
models a laser with mean energy ![]() in a volume
in a volume ![]() .
Photon number uncertainty
.
Photon number uncertainty![]() varies
inversely to phase uncertainty.
varies
inversely to phase uncertainty.
![]() (6.24a)
(6.24a) ![]() (6.24b)
(6.24b)
Amplitude
expectation value ![]() is zero for
is zero for ![]() states
due to incoherence of phase, but number
value
states
due to incoherence of phase, but number
value ![]() is exact as is proper frequency
is exact as is proper frequency ![]() due to the phase factor
due to the phase factor ![]() of
of
![]() .
.
A volume V
with ![]() -photons has energy
-photons has energy![]() or mass-equivalent
or mass-equivalent ![]() on a hyperbola
on a hyperbola ![]() quanta
above the N=1
hyperbola. A coherent-state
quanta
above the N=1
hyperbola. A coherent-state ![]() has
a mass
has
a mass ![]() with uncertainty
with uncertainty![]() so its phase uncertainty
so its phase uncertainty ![]() is low enough to make an (x,ct)-
grid (Fig. 6.6a) but a low-á state (Fig. 6.6c) has too
few photon counts-per-grid to plot sharply. Photon-number eigenstate
is low enough to make an (x,ct)-
grid (Fig. 6.6a) but a low-á state (Fig. 6.6c) has too
few photon counts-per-grid to plot sharply. Photon-number eigenstate ![]() in Fig. 6.6d is a total wash even for
high-N since
in Fig. 6.6d is a total wash even for
high-N since![]() implies maximal phase uncertainty (ÄÖ=į>>2ð).
implies maximal phase uncertainty (ÄÖ=į>>2ð).
Fig.
6.6 Simulated spacetime photon counts for coherent (a-c) and photon-number
states (d).
Deeper symmetry aspects of pair creation
Discussion
of relativity and quantum theory of wave amplitude requires further details.
This includes Dirac’s extraordinary theory that 2-CW light of certain
frequencies in a vacuum may create “real” matter that does not vanish when the
light is turned off. For example, we know that two 0.51MeV
č-ray photons of frequency
Ěe=mec2/h may create an electron and positron
“hole” that form positronium ![]() pairs. Also, 0.94GeV
č-rays with Ěp=mpc2/h may create proton-anti-proton
pairs. Also, 0.94GeV
č-rays with Ěp=mpc2/h may create proton-anti-proton![]() pairs, and so on.
pairs, and so on.
Dirac
creation processes raise questions, “What “cavity” traps 0.51MeV
č-pairs into stable ![]() pairs?” The discussion so far has only
begun to define 2-CW symmetry properties by phase rates in per-spacetime (K,Ű)-quantum variables. Conservation (5.2) of these
kinetic (K,Ű)-values implies that
pairs?” The discussion so far has only
begun to define 2-CW symmetry properties by phase rates in per-spacetime (K,Ű)-quantum variables. Conservation (5.2) of these
kinetic (K,Ű)-values implies that ![]() or
or![]() pairs
have the same (K,Ű)-values as the 2-CW light that
“creates” them.
pairs
have the same (K,Ű)-values as the 2-CW light that
“creates” them.
However, space-time symmetry arguments by themselves seem unable to derive internal lepton or baryon structure that might show how light becomes “trapped.” That question still lies beyond the scope of this discussion, and indeed, still largely beyond what is presently known. In fact, the current standard Weinberg-Salam model of high energy electroweak and strong quantum-chromo-dynamics (QCD) has abandoned the Dirac picture almost entirely. Pauli’s apparent dislike for Dirac may have had an effect.
In its place have there has arisen a large and controversial area known as super-symmetric-string-theory or “superstrings” that has generated over 10,000 publications in about 40 years and promised a “theory of everything” that would include quantum gravity. However, this flurry of mathematical activity has not yet yielded new experimental or physical insight nor has it provided a better way to study or teach existing areas of classical mechanics, relativity or quantum theory.
Two books give well written history of super-strings and related philosophy. One is by Lee Smolin and the other by Peter Woik. They show the presence at the highest academic levels of a rather pernicious group-think or make-believe that seems to have long given up the logical ideals of William of Occam.
L. Smolin, Trouble
in Physics: The rise of string theory and the fall of a science, Houghton-Miflin (New York 2006)
P. Woik, Not
even GNORW: The Failure of String Theory…, Persius Basic Books (New York 2006).
Chapter 7. Compton Effects and Optical Transitions
In Ch. 4-5 we found that space-time symmetry of a particle of mass M is like that of a 2-CW optical cavity wave of frequency Ě=Mc2/h. Here we relate 2-CW(k,Ě) “baseball diamond” Doppler shifts from Ch. 2-3 to light-matter collisions and scattering by molecules, atoms or nuclei. Doppler shifts are related to recoil shifts in 1-photon emission, 1-photon absorption, and 2-photon Compton scattering.
1-photon kinematics for emission and absorption of light
Photo-emission and photo-absorption allow you to see. In order to read this page, dye molecules in your eye absorb light emitted by atoms in a computer screen or lamp or other source such as the sun if you’re using daylight or moonlight. Without these processes we would all be blind.
There are several ways to describe and diagram emission and absorption by quantum levels. The first are Grotian level diagrams shown in Fig. 7.1a for a “quantum jump” between a molecular, atomic, or nuclear energy level-Em and a lower level-El. Each “jump” involves light at transition frequency Ěml that is the beat frequency ÄĚml=Ěm−Ěl between Planck frequency Ěm of level Em and Ěl of level El.
Em = hĚm (7.1a) El = hĚ l (7.1b)
Planck relation (4.5a) applies. We can only see beats or relative differences ÄĚml as noted vis-ą-vis (4.12).
Eml = h ÄĚml = hĚm−Ěl) = Em−El (7.1c)
Beat-frequency light is indicated by a wave emerging from a line connecting the energy level Em to El in Fig. 7.1a. A wavy single arrow going out (or in) indicates output emission (or input absorption).
Optical transitions have, quite literally, a “kicker.” Due to Axiom-1 (Ě=Īck), each 1-CW causing a frequency shift ÄĚml=Ěm−Ěl must come with a “kick” due to k-vector shift Äkml=(Ěm−Ěl)/. The kick or recoil by visible light is usually ignorable since 1/c is so tiny, but it is important for high-resolution spectra and for high-energy light such as č-rays. Grotian diagrams in Fig. 7.1a tend to obscure or ignore recoil.
Feynman diagrams in Fig. 7.1b show atomic K-vectors K=(Ě,ck) being kicked into K′=(Ě′,ck′) as atoms emit (or absorb) photons with vector ĚKęK=ĚKęK(Ī1,1). Baseball geometry in Fig. 7.2a fits vectors ĚKęK to connect low-level (Ěl) and mid-level (Ěm) hyperbolas and conserve total K-vector consistent with translation symmetry conservation rules of (5.19). Fig. 7.2b shows head-to-tail vector sum triangles.
K′= K− ĚKęK [emission] K′= K+ ĚKęK [absorption]
Vector Mę=(Ě,ck)=Ěm(coshĖ, sinhĖ) on Ěm-hyperbola in Fig. 7.2a has recoil rapidity Ė and invariant Ěm and rest energy Em =hĚm=Mmc2. Vector Lę on lower Ěl-hyperbola below Mę has the same Ė but lower El=hĚl. K-vector baseball diagram geometry follows directly from earlier Fig. 2.2 and Fig. 3.3.
This is not rocket science! (Or is it?)
Some quantum texts call photons “light bullets” since they have a “kick.” Doppler redshift relation Ěl =e−ĖĚm (top of Fig. 7.2a) shows atoms are like light-rockets. Consider invariant rest-mass ratio Mm/Ml.
Mm/Ml =Ěm/Ěl=e+Ė (7.2a) cŠ Ė =cŠln(Mm/Ml)~u (7.2b)
At low recoil (Ė ~u/c<<1) this is rocket equation (8.8b Unit 1) if “exhaust velocity” is light-speed c. By uncertainty relation ÄõŠÄt~1 high quality emission (low Äõ) means long time Ät to “exhaust” light.
Fig. 7.1 Quantum optical transitions represented by (a) Grotian and (b) Feynman diagrams.
______________________________________________________________________
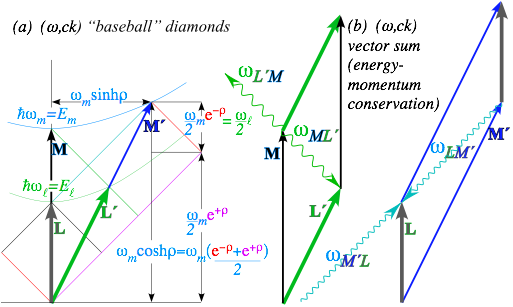
Fig. 7.2 Optical transitions displayed on (a) “Baseball diamond” and (b) Vector conservation sums.
A typical atomic transition (such as we use to read by) has a huge spectral quality (q) factor.
q=Ě0/2Ő=(angular resonant
frequency)/(transition decay rate)= Ě0ŠÄt =Ě0/ Äõ
Atomic q factors, discussed after (10.49) in Ch. 10 of Unit 1, range from 106 to over 108. The q qualifies a resonance by giving its amplification factor (over DC), its spectral purity, and its lifetime Ät in numbers of atomic beat periods or “heartbeats” it takes to complete a transition with 96% certainty. (Recall: e−ð~4%.)
High quality means a long “burn” to reduce an atomic mass energy from Em=Mmc2 to El=Mlc2, so maybe a rocket formula u~cŠln(Mm/Ml) makes sense. (Exact formula (7.2a) is Ė =ln(Mm/Ml).) Just saying quantum transitions are “jumps” misses a lot of physics. Getting there is (at least) half the fun!
2-photon processes: Rayleigh-Thompson-Compton scattering
Atomic 1-photon absorption shown in Fig. 7.1 is like an inelastic (“ka-runch”) SUV-VW collision in Fig. 1.1b or Fig. 2.1 of Unit 1. An atom (SUV) absorbs a photon (VW) to become more massive as it “jumps” from low level Ml to a higher mass Mm. While we just write off lost energy in SUV-VW crashes, the energy of atom plus light is conserved and time reversible. An SUV-VW cannot “uncrash” but atoms may emit light as well as absorb it. Atomic emission equation (7.2) is analogous to rocket propulsion.
An atomic 2-photon process of Compton scattering is sketched in Fig. 7.3a. It is like an elastic (“ka-bong”) SUV-VW collision in Fig. 2.2 of Unit 1. Atom-Ml (SUV) briefly absorbs the ĚKęK-photon (VW) but then just as quickly bounces it back as the atom recoils and returns to its initial Ml-level after emitting the photon. Fig. 2.2 of Unit 1 is in Center-of-Momentum COM frame as are the process diagrams in Fig. 7.3 where Äk-component of total-ÄK is zero. So, non-resonant Compton processes are a quick 1-2-punch.
An atomic 2-photon absorption process sketched in Fig. 7.3a is somewhat analogous to a 3-car pile-up. (See car crash in Fig. 8.5 of Unit 1.) However, wave time-energy uncertainty fuzzes auto-analogies. Pure (Ě,ck)-per-space-time pictures imply delocalization in classical space-time. CW (Ě,ck) represented in Fig. 7.1 thru Fig. 7.4 make CW space-time grids everywhere and forever. Nevertheless, scaled CW (Ě,ck) vectors overlap PW (x,ct)-paths as shown in Fig. 1.5 or Fig. 1.6 of Unit 1. Then Feynman (Ě,ck)-diagrams mimic (x,ct)-diagrams and K-arrows can represent PW (x,ct)-collision paths resembling car crashes.
However, with low-Ät PW paths comes fuzzy K-conservation. Time interval Ät and space Äx is large for initial and final vectors in Fig. 7.3a but not so for mid lines M or K. Thus intermediate (Ě,ck) values must be fuzzy and include combinations of non-resonant values known as virtual state sums.
Photon lines in Fig. 7.3a arise from diamonds in Fig. 7.4 that resemble a Ī45° baseball diamond used in Fig. 2.1 to develop relativity. However, the general diamond example in Fig. 7.4b differs in that 1st and 3rd bases are not on the light-cone baselines but suspended by vectors L and Lę like chopsticks pinch a piece of tofu. A new home plate lies at K(Ěk) above origin and 2nd base is at M(Ěm) above that. Pitcher’s-mound lies at L(Ěl) just below diamond center (as it does in regulation baseball). Half-sum-and-difference of invariant [Ěk, Ěl, Ěm] define a diamond with “rocket ratios” Ěm/Ěl=Ěl/Ěk=eĖ and geo-mean Ěl=√(ĚmŠĚk).
Diamond
center: ![]() ( Ěm+Ěk)
= Ěl coshĖ (7.3a) Diamond
radius:
( Ěm+Ěk)
= Ěl coshĖ (7.3a) Diamond
radius: ![]() ( Ěm-Ěk) = Ěl sinhĖ (7.3b)
( Ěm-Ěk) = Ěl sinhĖ (7.3b)
One exponential eĖ ratio defines a whole geometric series of hyperbola levels with equal recoil rapidity Ė.
Fig.
7.3 Level and Feynman diagrams of 2-photon processes: (a) COM Compton, (b) COM
absorption.
_________________________________________________________________
Fig.
7.4 3-level diamond connection map in (Ě,ck) per-spacetime. (b) COM example of
“kite.”
We now look at recoil effects in frames other than COM. We imagine we can “cut-and-paste” or create-and-destroy photon frequencies in the 2-CW cavity baseball diamond model of mass kinetics.
Right after Richard Feynman graduated from MIT his father asked a question, “Where is a photon before an atom emits it?” The question caught the new graduate off guard and it appeared that maybe a pricey MIT education was not worth all the money that his father had paid.[xx] Let us give a quantitative answer for Feynman’s father’s query using 2-CW optical analog for an atom that emits some of its “inner light” following its baseball-diamond geometry in Fig. 7.2.
To
apply baseball diamonds of Fig. 7.2 to an atom, we say it has the symmetry of 2-CW cavity state
represented by 2nd base![]() in the lower half Fig. 7.5a. A 1st
base K1=
in the lower half Fig. 7.5a. A 1st
base K1=![]() and 3rd base K3=
and 3rd base K3=![]() sum to an atom’s 2nd
base K2=
sum to an atom’s 2nd
base K2=![]() on a hyperbola of mass MQ
at Q.
on a hyperbola of mass MQ
at Q.
![]()
The pitcher’s mound P represents a 1-photon momentum-energy expectation value EP
at![]()
![]()
Point Q in Fig. 7.5a represents a 2-photon state of energy MQ=2EP.
In
Fig. 7.5a an emitted photon ![]() is
imagined being “cut” from 3rd base so
is
imagined being “cut” from 3rd base so ![]() shrinks by what we will call[xxi] a father-Feynman
factor ff as 3rd base alone loses the outgoing
shrinks by what we will call[xxi] a father-Feynman
factor ff as 3rd base alone loses the outgoing ![]() photon
energy.
photon
energy.
![]() (ff=1/4
in Fig. 7.5a.)
(ff=1/4
in Fig. 7.5a.)
If 1st
base stays at its old value![]() the 2nd base moves from Q on its initial 2ϖ-hyperbola
to
the 2nd base moves from Q on its initial 2ϖ-hyperbola
to ![]() on its final 2ϖ′ -hyperbola. Its new proper
frequency ϖ′ is a
geometric mean of 3rd and 1st as in Fig. 3.3.
on its final 2ϖ′ -hyperbola. Its new proper
frequency ϖ′ is a
geometric mean of 3rd and 1st as in Fig. 3.3.
![]() (7.4a)
(7.4a)
![]() (7.4b)
(7.4b)
![]() (7.4c)
(7.4c)
The
new 3rd base is a Feynman[xxii]redshift![]() of the new mean ϖ′ and a father-Feynman shift ff of
the old bases values
of the new mean ϖ′ and a father-Feynman shift ff of
the old bases values ![]() .
They are each an inverse-shift f -1 of the new mean ϖ′. The ff-shift
is a product of two f-shifts ff=f
2. This tricky notation is due to the Doppler derived group
multiplication rule (3.5c) for an
.
They are each an inverse-shift f -1 of the new mean ϖ′. The ff-shift
is a product of two f-shifts ff=f
2. This tricky notation is due to the Doppler derived group
multiplication rule (3.5c) for an ![]() and
an equal
and
an equal ![]() to
give composite
to
give composite ![]() .
.
In
Fig. 7.5a old 1st base and new 3rd base span a diamond of
rapidity![]() like Fig. 3.3b where
like Fig. 3.3b where![]() .
That redshift
.
That redshift ![]() in
Fig. 7.5a-c is another example of “rocket” mass ratio introduced in (7.2).
in
Fig. 7.5a-c is another example of “rocket” mass ratio introduced in (7.2).
Photo-absorption and Compton effects
The
factor![]() ,
chosen in Fig. 7.5a, cuts a fraction
,
chosen in Fig. 7.5a, cuts a fraction ![]() off the 3rd base photon
off the 3rd base photon![]() to
emit
to
emit ![]() and
reduces mass M2 by
factor
and
reduces mass M2 by
factor![]() to M1. Doppler factor f -1=2=eĖ
gives an atomic recoil boost of
to M1. Doppler factor f -1=2=eĖ
gives an atomic recoil boost of ![]() .
(Recall Fig. 2.2 where b=2
gives frame velocity
.
(Recall Fig. 2.2 where b=2
gives frame velocity ![]() .)
Mass M1 gets
that boost by absorbing
.)
Mass M1 gets
that boost by absorbing ![]() to
jump from P up to
to
jump from P up to ![]() in Fig. 7.5b. Inverse
in Fig. 7.5b. Inverse ![]() cut falls from Q to
cut falls from Q to![]() in
Fig. 7.5a. Paste
in
Fig. 7.5a. Paste ![]() onto 1st baseline in Fig. 7.5b
ups M1
to M2 on Ě′-axis
onto 1st baseline in Fig. 7.5b
ups M1
to M2 on Ě′-axis ![]() in Fig. 7.5c.
in Fig. 7.5c.
Fig.
7.5 Optical cavity model of (a) Emission, (b) Absorption, and (c) Compton
scattering
Final
Ě′-frame shift is b=eĖ
=2 of rapidity ![]() for either process. Emission
for either process. Emission![]() is
the final “cut” in a Compton “paste-and-cut”
is
the final “cut” in a Compton “paste-and-cut” ![]() process with the Feynman diagram in Fig.
7.6c. Its segments form an
process with the Feynman diagram in Fig.
7.6c. Its segments form an ![]() “kite” in Fig. 7.5c that is bent from a
symmetric kite
“kite” in Fig. 7.5c that is bent from a
symmetric kite ![]() by the boost
by the boost ![]() of the main kite OQ-axis relative to
either of its wings
of the main kite OQ-axis relative to
either of its wings ![]() or
or ![]() .
Each kite is a suspended baseball diamond like Fig. 7.4b or a boosted Ė-warped version of
one.
.
Each kite is a suspended baseball diamond like Fig. 7.4b or a boosted Ė-warped version of
one.
Both “paste-and-cut”![]() and reverse “cut-and-paste”
and reverse “cut-and-paste”![]() processes in Fig. 7.6 entail total recoil
boost
processes in Fig. 7.6 entail total recoil
boost ![]() from the lab
from the lab![]() axis to an
axis to an ![]() axis of the Compton scattered atom in
Fig. 7.5c. The latter first “cuts” down to point O′ on a
axis of the Compton scattered atom in
Fig. 7.5c. The latter first “cuts” down to point O′ on a ![]() -hyperbola by emitting photon
-hyperbola by emitting photon![]() before absorbing the
before absorbing the ![]() photon that comes first in the former
sequence.
photon that comes first in the former
sequence.
An
inverse Compton process ![]() emits
photon
emits
photon![]() (as
in Fig. 7.5a) then absorbs photon
(as
in Fig. 7.5a) then absorbs photon ![]() that
moves it from rapidity Ė on hyperbola-
that
moves it from rapidity Ė on hyperbola-![]() to
rapidity 2Ė on hyperbola
to
rapidity 2Ė on hyperbola![]() at point
at point ![]() (upper
right of Fig. 7.5c). Here a fixed mass
(upper
right of Fig. 7.5c). Here a fixed mass![]() emits
emits
![]() to gain speed
to gain speed![]() by
reducing its mass to
by
reducing its mass to![]() then recovers mass by absorbing
then recovers mass by absorbing ![]() to end up at an even faster speed
to end up at an even faster speed![]() .
.
Photon K-vectors for any Compton process between 2:1-rest mass hyperbolas make a Ė-warped baseball diamond with Ė=ln2 according to (7.5) as shown in Fig. 7.5c and Fig. 7.6a. Like a 2:1-Doppler diamond in Fig. 3.3b, it has an aspect ratio that is twice its blue-shift b=eĖ =2, that is 2eĖ =4.
A 2:1-rest mass drop shows geometry more clearly than a realistic ratio 1010:1010-1 for an atomic transition that is about 10-10 of rest mass. Atomic rest-energy level ratios Em: Eh are close to unity and fortunately so for our health! Harmonic levels with integral m:h ratios used in Fig. 7.5 apply to optical-cavity models but m and h are small integers only for special spectra like Rydberg or rotor transitions.
In
going from higher hyperbola ![]() to middle
to middle ![]() the
lab recoil shift is
the
lab recoil shift is![]() by (7.5), and its emitted frequency
by (7.5), and its emitted frequency ![]() is the altitude of a kite triangle, like
is the altitude of a kite triangle, like ![]() in
Fig. 7.5c, given as follows.
in
Fig. 7.5c, given as follows.
![]() (7.6)
(7.6)
The example in Fig. 7.5a has ![]() .
Doppler shifts of
.
Doppler shifts of ![]() by
by
![]() form a geometric series
form a geometric series ![]() of steps on a Compton staircase
of steps on a Compton staircase![]() between
(2:1)-levels
between
(2:1)-levels
![]() and
and![]() in Fig. 7.5c. For any rational level ratio
in Fig. 7.5c. For any rational level ratio![]() ,
each dilation factor
,
each dilation factor![]() ,
recoil
,
recoil![]() ,
or ratio
,
or ratio![]() is a rational ratio, too, and the
Pythagorean sum
is a rational ratio, too, and the
Pythagorean sum ![]() belongs to a rational triangle, e.g.,
belongs to a rational triangle, e.g.,![]() .
.
![]() (7.7a)
(7.7a)
![]() (7.7b)
(7.7b) ![]() (7.7c)
(7.7c)
Recoil
trims emitted![]() below Ä=|h-m|ϖ by a factor (h+m)/2h while absorption
below Ä=|h-m|ϖ by a factor (h+m)/2h while absorption ![]() costs more than Ä
by a factor (h+m)/2m.
Newtonian recoil
costs more than Ä
by a factor (h+m)/2m.
Newtonian recoil![]() is a circle of radius
is a circle of radius![]() in Fig. 7.5, so even low-u recoil costs a little.
Photons, like money-changing tourists, get nicked coming and going.
in Fig. 7.5, so even low-u recoil costs a little.
Photons, like money-changing tourists, get nicked coming and going.
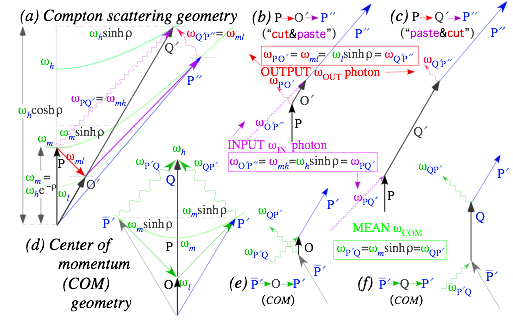
Fig. 7.6 Compton scattering. (a) Vector sums on mass hyperbolas of low Ěl , medium Ěm , and high Ěh. (b-c) Feynman graphs. (d) Center of Momentum (COM) vector sums. (e-f) COM Feynman graphs.
An
absorption (m<h)
frequency![]() is
greater than emission
is
greater than emission![]() by a factor
by a factor![]() .
A Compton
.
A Compton ![]() due
to
due
to ![]() is less than
is less than![]() by the inverse factor
by the inverse factor ![]() .
Hence a Compton output
.
Hence a Compton output ![]() is less than its input
is less than its input ![]() by
the Doppler ratio-square
by
the Doppler ratio-square![]() as shown before.
as shown before.
![]() ,
, ![]() (7.8)
(7.8)
Compton processes in Fig. 7.6 start on middle ![]() hyperbola to do a 2-photon bounce off a
lower
hyperbola to do a 2-photon bounce off a
lower ![]() or a higher
or a higher ![]() hyperbola.
An intermediate “bouncer” is said to be a virtual
level if its Ěl or Ěh
values are integration variables being summed. A process
hyperbola.
An intermediate “bouncer” is said to be a virtual
level if its Ěl or Ěh
values are integration variables being summed. A process ![]() or
or
![]() is
said to be a resonant Compton process if an h-state or l-state exists. Whether numbers m, h
, and l are
integers in a cavity model or real values for an atomic model, the results
(7.6), (7.7), and (7.8) apply in any case.
is
said to be a resonant Compton process if an h-state or l-state exists. Whether numbers m, h
, and l are
integers in a cavity model or real values for an atomic model, the results
(7.6), (7.7), and (7.8) apply in any case.
Inverse
frequencies ![]() give the famous Compton wavelength sum
rule.
give the famous Compton wavelength sum
rule.
![]() , or:
, or: ![]() where:
where: ![]() . (7.9)
. (7.9)
Compton radius![]() is
a minimum cavity radius with a frequency equal to the “zwitterbevegun”
of mass
Mm. As input
is
a minimum cavity radius with a frequency equal to the “zwitterbevegun”
of mass
Mm. As input ![]() reflects from an Mm-cavity it picks up
diameter
reflects from an Mm-cavity it picks up
diameter![]() to
become
to
become ![]() .
Size
.
Size ![]() depends on mass Mm of level-m, not
on Mh
or Ml
of higher level-h
or lower level-l that bounces level-m.
depends on mass Mm of level-m, not
on Mh
or Ml
of higher level-h
or lower level-l that bounces level-m.
Compton
radius ![]() is a curious inverse measure of mass
size. Larger mass M has a
smaller
is a curious inverse measure of mass
size. Larger mass M has a
smaller ![]() size
that recoils less and reflects photons more elastically. Elastic mirror
reflection is what we expect in classical wave optics where light is assumed to
be as “light” as anything can be.
size
that recoils less and reflects photons more elastically. Elastic mirror
reflection is what we expect in classical wave optics where light is assumed to
be as “light” as anything can be.
A
geometric![]() -series
-series![]() of
levels also has a geometric series
of
levels also has a geometric series ![]() of transitions.
This gives Compton “nets” such as the
of transitions.
This gives Compton “nets” such as the ![]() -net
in Fig. 7.7a or a finer
-net
in Fig. 7.7a or a finer ![]() -net
in Fig. 7.7b. Finer fractions (f
-net
in Fig. 7.7b. Finer fractions (f
![]() 1) give smaller jumps and
acceleration that is more continuous and constant.
1) give smaller jumps and
acceleration that is more continuous and constant.
An
acceleration of space-time frames by geometric or exponential frequency
chirping is described in Chapter 8. Space-time grid in Fig. 8.2 has a geometric
spacing like the Compton nets in Fig. 7.7 but with a (P,G)![]() (P,G) axis switch and is
an optical version of Einstein’s famous thought experiment.
(P,G) axis switch and is
an optical version of Einstein’s famous thought experiment.
Optical PW bounce and accordian-like CW shifts
If the Ě vs ck net plots in Fig. 7.7 were instead space-time ct vs x plots one could imagine each vertically sloping line is a path of an object moving at constant rapidity Ė away from the stationary (Ė=0) time ct-axis of the lab frame. Each hyperbola in Fig. 7.7a crosses a path at proper times ô=… ô, 2ô, 4ô,… that are local times on each object’s ct′-axis given eĖ=f=2. For general f=eĖ, the times are ô=…ô, fô, f2ô, f3ô, ….
Imagine each Ī45° photon line is part of a PW light path reflecting back and forth between the lab ct-axis and the object ct′-axis. Let the lab and moving frame have reflecting mirrors to receive light of a certain frequency (for CW) or a band of frequencies (for PW) and reflect it back and forth between them.
If
mirror-1
sends out wavelength Ď0, mirror-2 sees it as a Doppler red-shifted
wavelength Ď1 = Ď0eĖ that it promptly returns to mirror-1 who sees another red-shift
factor eĖ tacked on to give Ď2 = Ď1eĖ= Ď0e2Ė. Locally observed refection times ôk and reflected
wavelengths Ďk both form geometric
series …1,
f, f2,
f3,…
ôk =(…ô, ô1, ô2, ô3, …) =(…ô, fô, f2ô, f3ô, …) =ô(…1, f, f2, f3, …) (7.10a)
Ďk =(…Ď, Ď1, Ď2, Ď3, …) =(…Ď, fĎ, f2Ď, f3Ď, …)=Ď(…1, f, f2, f3, …) (7.10b)
Resulting space-time zigzag paths in Fig. 7.8a have even “zig” reflections (k=…0, 2, 4,…) off the stationary lab mirror-1 and odd “zag” reflections (k=…1, 3, 5,…) off mirror-2. Fig. 7.8b has added counter-propagating odd-time “zag” and even-time “zig” reflections to frame rectangular diamond-k whose 1st and 3rd bases lie at time ôk for lab mirror-1 and mirror-2. Its 2nd and home base lie on a line of rapidity half that of mirror-2 with red-shift eĖ/2=√f=21/2 in Fig. 7.8b. Diamond-k 2nd-base is home base for diamond-(k+1).
The space-time analog of “rocket” relations (7.2) is ôk+1/ôk=e+Ė=ôk/ôk-1. Reflection path-nets also have half-sum-and-difference relations analogous to (7.3) and geometric mean relations ôk=√( ôk+1Š ôk-1). This is used to slice reflection time intervals into units of 21/2ô0 or 21/4 ô0 as is done in Fig. 7.8b, and this gives lines of rapidity Ė/4, 2Ė/4,3Ė/4, and Ė, with red-shifts 21/4, 22/4, 23/4, and 2, respectively.
Ideal light bounces in Fig. 7.8 and mass bounces in Fig. 6.7 of Unit 1 share some key properties. While they change energy without limit, both conserve action perfectly. For a light cavity made of mirror-1 and mirror-2, action is an integral number n of 1/2-waves that is shown for n=4 in Fig. 7.8b where CW nodes move Ė/n faster than the one behind and Ė/n slower than one ahead. Adiabatic n invariance is the rule for quantum wave systems and applies to photon number N, too. But, rules are made to be broken!
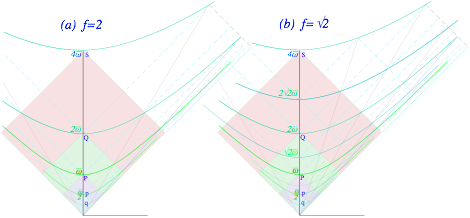
Fig. 7.7 Compton nets are congruent
Compton staircases of transitions. (a) f=2:1 (b) f=![]() :1
:1
_____________________________________________________________________

Fig. 7.8 Space-time nets (a) PW zigzag paths bounce. (b) CW nodes squeeze like an accordian.
Chapter 8. Wave Frame Acceleration
Here we turn the hyperbola geometry of space-time Fig. 7.8 on its side to expose an accelerating wave frame made by CW, PW, or intermediate wave fields. This provides a coherent interference view of the Einstein elevator gedankken (thought) experiment. Like many such experiments of imagination, there are quite a few practical details left out. So it may be some time before we can actually do them!
Chirping and Einstein elevators
A spacetime version of Compton nets are curved coordinates for accelerated Einstein elevators and this helps to visualize equivalence principles for general relativity.[xxiii] Plots in Fig. 8.1 and Fig. 8.2 show waves from chirping tunable lasers forming colorful renderings of hyper-net coordinates.
A
previous Fig. 2.2c plotted an atom (x′,ct′)-view of it running head-on at
rapidity Ė into a green ![]() -beam that is blue (
-beam that is blue (![]() e+Ė) shifted while the receding laser appears red (
e+Ė) shifted while the receding laser appears red (![]() e−Ė) shifted. The laser (x,
ct)-grid then appears as a Ė-tipped Minkowski grid. If instead the lasers had been tuned to
frequencies
e−Ė) shifted. The laser (x,
ct)-grid then appears as a Ė-tipped Minkowski grid. If instead the lasers had been tuned to
frequencies ![]() e−Ė and
e−Ė and ![]() e+Ė, respectively, the (u=ctanh Ė)-moving atom would see beams of green
e+Ė, respectively, the (u=ctanh Ė)-moving atom would see beams of green ![]() −light
waves interfering to make a square (Ė=0) Cartesian
(x, ct)-grid like Fig. 2.1c.
(Amplitude would also be tuned along with frequency if we wanted to squelch the
wave galloping shown in Fig. 6.2 and Fig. 6.3.)
−light
waves interfering to make a square (Ė=0) Cartesian
(x, ct)-grid like Fig. 2.1c.
(Amplitude would also be tuned along with frequency if we wanted to squelch the
wave galloping shown in Fig. 6.2 and Fig. 6.3.)
Varying tuning parameter Ė of the lasers changes local grid rapidity Ė at the beams’ spacetime intersection as sketched in Fig. 8.1a-b. This produces a curved space-time coordinate system of paths with rapidity changing just so both beams end up always the same color on any given trajectory.
Each
trajectory plotted in Fig. 8.2 has its own constant proper acceleration g and local color ![]() . A
mass M
following such a x(t)-path
has a K
that follows its M-hyperbola
in Fig. 7.7. The lasers each send waves that meet at each trajectory point x(t)
and paint a local interference grid of varying rapidity Ė on a trajectory x(t)
of varying velocity u(t)
given by (6a) and sketched in Fig. 8.1a.
. A
mass M
following such a x(t)-path
has a K
that follows its M-hyperbola
in Fig. 7.7. The lasers each send waves that meet at each trajectory point x(t)
and paint a local interference grid of varying rapidity Ė on a trajectory x(t)
of varying velocity u(t)
given by (6a) and sketched in Fig. 8.1a.
![]() (8.1)
(8.1)
Setting x′=0 and t′=ô in (2.21) relates proper time interval dô to lab dt . This gives x(t) by ô-integrals.
![]() (8.2a)
(8.2a)
![]() (8.2b)
(8.2b)
![]() (8.2c)
(8.2c) ![]() (8.2d)
(8.2d)
Path x(t) depends on Ė(ô) variation in proper ô. Linear rate u~gô or Ė=ô/c gives a hyperbolic path in Fig. 8.1b of fixed proper acceleration g and a family of concentric paths of different g in Fig. 8.2.
![]() (8.3a)
(8.3a) ![]() (8.3b)
(8.3b)
Paths closer to the left hand blue-chirping laser have a higher g than flatter ones nearer the red-chirping right hand source. Ė-skewed baseball diamonds of PW and CW paths in lower Fig. 8.2 are spaced geometrically along the x-axis of a spaceship at a moment when its lab-relative rapidity is Ė=0.2.
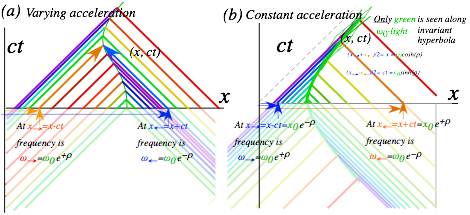
Fig. 8.1 Optical wave frames by
red-and-blue-chirped lasers (a)Varying acceleration (b)Constant g.
Geometric eĪĖ-variation (8.3) of wave and coordinate spacing is due to a left-hand laser’s right-moving wave of frequency Ě→=Ě0e+Ė on light cone x→=x-ct=x0e−Ė and a right-hand laser’s left-moving wave of frequency Ě←=Ě0e−Ė on light cone x←=x+ct=x0e+Ė. Wave interference does the rest.
Initial (Ė=0) position of hyperbola Ě0 is l0=x0=c2/g0. Each hyperbola has different but fixed location l, color Ě, and artificial gravity g that, by (8.3), are proper invariants of each path.
x2-(ct)2 = l2 , where: l=c2/g (8.4)
Frequency Ě and acceleration g vary inversely with the path’s proper location l relative to origin.
Ě l =Ě c2/g =Ě0 c2/g0 = const. (8.5)
Rapidity Ė=ô/c in (8.3) has proper time be a product of hyperbolic radius l in (8.4) and “angle” Ė.
cô = Ė c2/g = l Ė (8.6)
This is analogous to a familiar circular arc length formula s = r ö. Both have a singular center.
The
less familiar hyperbolic center (x,ct)=(0,0)
here begins an elementary event horizon. The blue-chirp laser would need infinite frequency Ě0e+Ė at origin where ct=e−Ė goes to zero, so it gives up before
t=0. After t=0,
light from the laser to any path S or T
given by (8.3) never arrives. Fig. 8.2 shows paths of a spaceship S and a “trailer” T trailing by invariant length lST=l(S)-l(T) on an x-axis
of rapidity Ė through origin (x,ct)=(0,0).
S and T always have the same
velocity (8.1) relative to the lab, maintain proper interval![]() ,
but trailer T feels
greater g. Lower parts of a rigid rod accelerate more, and this gives
the lab-observed Lorentz length-contraction indicated at the top of Fig. 8.2.
,
but trailer T feels
greater g. Lower parts of a rigid rod accelerate more, and this gives
the lab-observed Lorentz length-contraction indicated at the top of Fig. 8.2.
In a Newtonian paradigm, asymmetric acceleration seems paradoxical, but if waves make a coordinate frame, asymmetry is a consequence of the DeBroglie relation (4.5b) between k-vector and momentum. Accelerating frames require shortening wavelength and this crowds waves.
Wave properties also manifest the accelerated frames’ upstairs-downstairs disparity in proper time ô (“later” upstairs by (8.6)) and shift in frequency Ě (lower or “red shifted” upstairs by (8.5)). Along nodal (white) lines that are the ship-trailer x-axis for a momentary rapidity Ė, wave phase is seen to be some constant kl−Ěô=Íð/2. The Einstein equivalence of gravity to an accelerated elevator is manifested by a gravitational red shift and an increase of clock rates in the upstairs regions of a field.
A quantized version of Fig. 8.2 would be an atom with a transition at ĚI, undergoing a sequential resonant Compton scattering of exponentially chirped photons ĚI, eĪĖĚI, eĪ2ĖĚI, eĪ3ĖĚI,… between the same pair of hyperbolas in Fig. 8.2. The atom sees the same color and feels the same recoil rapidity at each step in the quantum version of constant acceleration.
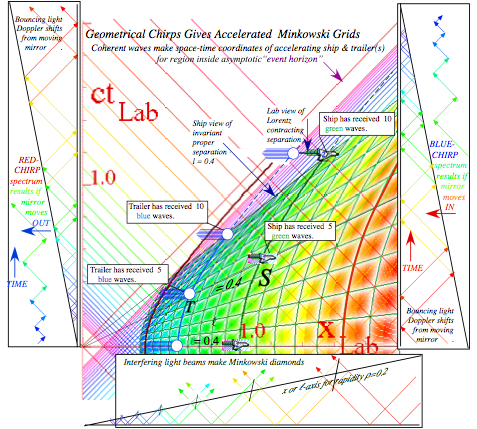
Fig.
8.2 Accelerated reference frames and their trajectories painted by chirped
coherent light
Constant velocity gives constant acceleration
This leads one to ask if chirped light might be used for atomic or molecular acceleration. Logarithmic dependence Ė=ln b of rapidity on Doppler b favors ultra-precise low energy acceleration, more appropriate for nanotechnology than high-energy acceleration with its extreme bandwidth.
The flip symmetry between two sides of a light cone suggests optical cavities with a geometric chirp. If you flip the diamond sequence in lower Fig. 8.2 across the light cone to the sides of Fig. 8.2 you get spacetime light paths bouncing between mirrors moving relative to each other as analyzed in Fig. 7.8.
As mirrors close, trapped light blue-chirps exponentially as on the right side in Fig. 8.2. It red-chirps if the two mirrors separate as they do on the left side of Fig. 8.2 and in Fig. 7.8. Together, a desired eĪnĖ spectrum could in principle be made by translating one etalon cavity at constant velocity relative to another stationary cavity that is enclosed by the translating one. In this way, light generated by mirrors of constant velocity provides the spectrum needed to make an interference net of constant acceleration. Coherent acceleration like Fig. 8.2 (but slower) might be done with precision needed for laser metrology.
Wave geometry ought to make us more skeptical of the coordinate boxes and manifolds that have been our paradigm for centuries. A common image is the Newton-Descartes empty-box at some absolute time existing whether or not it contains any “particles.” We first learn to picture spacetime coordinates as a giant metal frame of clocks like Fig. 9 in Taylor and Wheeler’s[xxiv] relativity text. That figure is more like a parody of common views of spacetime manifolds that remain with us to this day. Such a monstrosity of a framework is decidedly nonexistent and non-operational. Current metrology uses light waves.
A wave frame like Fig. 2.1, Fig. 2.2, or Fig. 8.2 is physical metrological coordinate system whose geometry and logic arises from the light that makes it. The things being coordinated (waves) have their own coordinates and dynamics built in. Einstein general theory of relativity trumped Newton’s box by showing how it is affected (curved) by any energy or mass it holds. Quantum theory seems to go a step further by indicating that this box and its contents should be viewed as one and the same thing.
Pair creation and quantum frames.
Dirac,
before others, realized that per-spacetime has the symmetry of spacetime. Past
and future (time-reversal) symmetry demands negative frequency as well as positive. In order
to visualize Dirac’s pair-creation process we extend the playing field to
back-to-back baseball-diamonds with four nets of invariant hyperbolas. Examples
of pair-creation are sketched in Fig. 8.3 as seen from two different reference
frames. Pair creation-destruction is then seen a strange sort of Compton
process in which the “photon diamond” of Fig. 7.4 is centered at the light
baseline intersection with 2nd base at +mc2
and home base at -mc2 and 1st and 3rd bases on ĪG-hyperbolas.
The
Feynman graph of Compton scattering in Fig. 7.6c-d is turned on its side in
Fig. 8.3 so it may start and end on different branches of the m-hyperbola corresponding to mass Īm. Two photons, whose energy sum equals
the energy gap 2mc2, appear to bounce off intermediate
hyperbolas in Fig. 8.3 that are conjugate hyperbolas defining group wavevectors
Kg in Fig. 2.1 or 2.2. Such dispersion is said to belong to instanton or tachyon waves of imaginary frequency Īi![]() that entails a huge damping factor
that entails a huge damping factor ![]() that proscribes their direct observation.
They are said to be in the virtual or intermediate realm.
that proscribes their direct observation.
They are said to be in the virtual or intermediate realm.

Fig. 8.3 Dirac
matter-antimatter dispersion relations and pair-creation-destruction processes.
Dirac’s
is the first quantum theory to fully incorporate relativity. It introduces dual
anti-worlds, in which all three mass definitions (3.6), (3.7), and (3.9) have
negative values, but leaves many questions about their physical meaning.
Analogies between the ![]() process in Fig. 8.3 and exciton formation
in the band theory of solids, shed some light on the physics. However, the
exciton process is a straight-up 1-photon process whose momentum is tiny compared
to the energy jump, and it lacks the world-anti-world symmetry of the Dirac
exciton in which both the electron and an anti-electron have the same group
velocity but opposite momentum. The Dirac model has duality of reversed energy
(frequency), momentum (k-vector),
space, and time that is quite extraordinary.
process in Fig. 8.3 and exciton formation
in the band theory of solids, shed some light on the physics. However, the
exciton process is a straight-up 1-photon process whose momentum is tiny compared
to the energy jump, and it lacks the world-anti-world symmetry of the Dirac
exciton in which both the electron and an anti-electron have the same group
velocity but opposite momentum. The Dirac model has duality of reversed energy
(frequency), momentum (k-vector),
space, and time that is quite extraordinary.
A
number of implications of Dirac’s theory have been mostly ignored. There is an
unwillingness to abandon vestigial concepts associated with absolute classical
frames, manifolds, or “boxes.” However, quantum frames are like all things
quantum mechanical and have an intrinsic relativity associated with their wavelike
interference. Quantum frames, as they are used in molecular and nuclear
physics, are known to have internal or body-relative parts in addition to the
more commonly known external or laboratory-relative parts. This inside-and-out
duality is a deep quantum mechanical result arising first in the theory of
quantum rotors by Casimir, but it also underlies Lorentz-Poincare symmetry that
includes locally rotating frames as well as translating ones.
Indeed,
the quantum theory of angular momentum has a built-in duality that is as
fundamental as the left-and-right or bra-and-ket duality of the conjugate parts
of Dirac’s elegant quantum notation ![]() . The Wigner
. The Wigner ![]() –functions are quantum rotor
wavefunctions
–functions are quantum rotor
wavefunctions ![]() that have their external laboratory m-quantum numbers on the left and their
internal or body n-quantum numbers on the right. Their J-multiplicity is thus
(2J+1)-squared and not simply the (2J+1) so familiar in elementary Schrodinger
quantum theory of atomic angular momentum.
that have their external laboratory m-quantum numbers on the left and their
internal or body n-quantum numbers on the right. Their J-multiplicity is thus
(2J+1)-squared and not simply the (2J+1) so familiar in elementary Schrodinger
quantum theory of atomic angular momentum.
It
took many years for classical physics to fully accept Einstein’s translational
relativity principles. Perhaps, if the wave nature of quantum physics had
already been established, the relativistic axioms would have been seen as an
immediate consequence of wave interference. Indeed, these two subjects are,
perhaps, too closely related for that to have
happened.
Now
quantum theory demands a more general kind of relativity involving rotation and
other accelerations that is a step beyond the special relativity of constant
velocity. This brings up a quite controversial area first explored by Ernst Mach,
the originator of Mach’s Principle. Mach made the seemingly impossible
proposal that centrifugal forces, the kind physicists assign the label ficticious
force,
are somehow due to their relativity to all matter in the universe.
Mach’s
idea may sound silly, but a kind of quantum Mach’s Principle is needed to
understand spectra and dynamics of quantum rotor![]() waves even in the non-relativistic limit.
We are unaware of any fully relativistic quantum treatment of such systems, and
it is not clear what if anything would be the cosmological implication of such
a grand relativistic quantum wave mechanics. Nevertheless, it seems that the
dual 4-by-4 wave-anti-wave space of Dirac is one of the first to re-examine.
waves even in the non-relativistic limit.
We are unaware of any fully relativistic quantum treatment of such systems, and
it is not clear what if anything would be the cosmological implication of such
a grand relativistic quantum wave mechanics. Nevertheless, it seems that the
dual 4-by-4 wave-anti-wave space of Dirac is one of the first to re-examine.
Physics
is still at a stage where large-scale phenomena use Newton-Einstein
particle-in-manifold theory while small-scale phenomena employ
Planck-DeBroglie-Schrodinger wave field theory. However, both employ some form
of space and time coordinates. In this they share an enigma whose existence is
largely unquestioned. Supposed invariance to reference frame definition is
taken to mean that underlying frames don’t matter.
That
leaves our fundamental metrology in a dysfunctional dysphoria of an ignored
spouse, indispensable, but having only marginal identity. If Evenson and
Einstein have taught us anything, it is that this has to be a mistake. Frames do matter! The results of Dirac and many
others have shown they make matter and indeed are our matter.
[1] K. M. Evenson, J.S.
Wells, F.R. Peterson, B.L. Danielson, G.W. Day, R.L. Barger and J.L. Hall,
Phys. Rev. Letters 29, 1346(1972).
[1] Guinness Book of
Records (1973).
[1] Glauber, Roy J., Hall,
John L. and Hansch, Theodor W. The Nobel Prize in Physics, 2005. http://nobelprize.org/
[1] J.
L. Hall and T. Hensch, Opt. Lett. 9, 502-504 (1984).
[1] N. Ashby, Physics Today, 55(5): 41 (May 2002).
[1] J.
L. Hall, Laser Spectroscopy VII,(T. W. Hansch and Y. R. Shen, Eds.,
Springer-Verlag, 1985), pp. 393-394.
[1] William of Occam
(1245-1326) “Pluralitas
non est ponenda sine neccesitate” (Do not assume plurality without
necessity.)
[1] A. Cho, Science 306, 1461 (2004).
[1] A. Einstein, Annalen
der Physik 17,891(1905). (Translation by W. Perrett and G.B. Jeffery, The Principle of Relativity(with notes by A.
Sommerfield) (Methuen, London 1923), (republished by Dover, London 1952).
[1] W. G. Harter, J. Mol.
Spectrosc. 210, 166(2001).
[1] W. G. Harter, J. Evans,
R. Vega, and S. Wilson, Am. J. Phys. 53, 671(1985).
[1] W.G. Harter and T. C.
Reimer, //www.uark.edu/ua/pirelli/html/poincare_inv_2.htm
[1] D. E. Herschbach,
(unpublished, 2005).
[1] H. Minkowski, Mathematisch-Physikalische
Klasse, vol. 1, 53 (1908).
[1] H. A. Lorentz
Koninklijke Akademie vanWetenschappen te Amsterdam. Section of Science. Proc.
6: 809-831 (1904).
[1] Albert Einstein "Zur Elektrodynamik bewegter Korper." Annalen der Physik
18,639 (1905); Annalen der Physik 17,891(1905). (Translation: Perrett and
Jeffery, The Principle
of Relativity, (Methuen, London 1923), (Dover, 1952).
[1] Max Planck "Zur Theorie des Gesetzes der Energieverteilung im
Normal-spectrum." Deutsche Physikalische Gesellschaft. Verhandlungen 2:
237-245 (1900).
[1] Louis de Broglie,
Nature 112, 540 (1923); Annalen der Physik (10) 2 (1923).
[1] P. A. M. Dirac, “Forms
of Relativistic Dynamics” Rev. Mod.
Physics, 21: 392 (1949).
[1] Albert Einstein "Uber einen die Erzeugung und Verwandlung des Lichtes
betreffenden heuristischen Gesichtspunkt." Annalen der
Physik 17: 132-148 (1905). (Translation by A.B. Aarons and M.B. Peppard, Am. J.
Phys. 33, 367(1965).)
[1] E. Schrodinger, Annalen
der Physik (4) 79 361 and 489 (1923); 80, 437 (1926); 81,109 (1926).
[1] Schrodinger’s protests
about prevailing quantum mechanical interpretations are widely circulated. So
far we have been unable to locate more solid references.
[1] N. Bohr, Zeitschrift
fur Physik, 9, 1-2, (1922).
[1] W. Heisenberg, The Physical Principles of the Quantum Theory, (Dover, New York,
1930).
[1] P.A.M. Dirac, Lectures on quantum
mechanics, (New York, Belfer
Graduate School of Science, Yeshiva University, 1964). Dirac’s first text in
1931 used á and Č to denote bra-ket duality.
[1] A. Einstein, "I shall never believe that god plays dice with the
universe" Albert Einstein Archives, The Jewish National & University
Library, The Hebrew University of Jerusalem (www.albert-einstein.org), Einstein
Archives Online, Volume 15, #294, Letter to Cornelius Lanczos, March 21,
1942,http://www.alberteinstein.info/db/ViewDetails.do?DocumentID=30893.
[1] R. Feynman, The Pleasure of Finding Things Out, (Perseus Publishing,
Cambridge, MA,1999) p. 8.
[1] (unpublished) A huge energy shift is used for sake of geometric clarity.
Atoms usually lose less than one part in 109 or 1010 of
their rest mass in optical emission. The atom in the example loses rest mass
1/2 M2c2
emitting a 3/8 M2c2 photon.
[1] R. P. Feynman, R.
Leighton, and M. Sands, The Feynman
Lectures (Addison Wesley 1964) Our development owes a lot to
Feynman’s treatment cavity wave dispersion in Vol. II Ch. 24 and Vol. III Ch.
7.
[1] W. Rindler, Essential Relativity-Special, General, and Cosmological, Springer (New York
1977) p. 18. See also ref. 8, p. 111.
[1] E.F.Taylor and J.A. Wheeler, Spacetime Physics (W. H. Freeman San
Francisco 1966) p. 18.
The
author would like to thank Ronald F. Fox and Eric J. Heller for careful reading
and suggestions regarding early versions of this work and Daniel Kennefick for
information from the Einstein Centennial bibliography project. Also, I
appreciate many years of discussion with John E. Heighway about aspects of
special and general relativity. Finally, I am grateful to Molly Longstreth and
Usha Gupta for help with general bibliographic search.
-- The Purest Light and a Resonance Hero – Ken Evenson (1932-2002) --
When travelers punch up their GPS coordinates they owe a debt of gratitude to an under sung hero who, alongside his colleagues and students, often toiled 18 hour days deep inside a laser laboratory lit only by the purest light in the universe.
Ken was an “Indiana Jones” of modern physics. While he may never have been called “Montana Ken,” such a name would describe a real life hero from Bozeman, Montana, whose extraordinary accomplishments in many ways surpass the fictional characters in cinematic thrillers like Raiders of the Lost Arc.
Indeed, there were some exciting real life moments shared by his wife Vera, one together with Ken in a canoe literally inches from the hundred-foot drop-off of Brazil’s largest waterfall. But, such outdoor exploits, of which Ken had many, pale in the light of an in-the-lab brilliance and courage that profoundly enriched the world.
Ken is one of few researchers and perhaps the only physicist to be twice listed in the Guinness Book of Records. The listings are not for jungle exploits but for his lab’s highest frequency measurement and for a speed of light determination that made c many times more precise due to his lab’s pioneering work with John Hall in laser resonance and metrology†.
The meter-kilogram-second (mks) system of units underwent a redefinition largely because of these efforts. Thereafter, the speed of light c was set to 299,792,458ms-1. The meter was defined in terms of c, instead of the other way around since his time precision had so far trumped that for distance. Without such resonance precision, the Global Positioning System (GPS), the first large-scale wave space-time coordinate system, would not be possible.
Ken’s courage and persistence at the Time and Frequency Division of the Boulder Laboratories in the National Bureau of Standards (now the National Institute of Standards and Technology or NIST) are legendary as are his railings against boneheaded administrators who seemed bent on thwarting his best efforts. Undaunted, Ken’s lab painstakingly exploited the resonance properties of metal-insulator diodes, and succeeded in literally counting the waves of near-infrared radiation and eventually visible light itself.
Those who knew Ken miss him terribly.
But, his indelible legacy resonates today as ultra-precise atomic and molecular
wave and pulse quantum optics continue to advance and provide heretofore
unimaginable capability. Our quality of life depends on their metrology through
the Quality and Finesse of the resonant oscillators that are the heartbeats of
our technology.
Before being taken by Lou Gehrig’s
disease, Ken began ultra-precise laser spectroscopy of unusual molecules such
as HO2, the radical cousin of the more common H2O. Like
Ken, such radical molecules affect us as much or more than better known ones.
But also like Ken, they toil in obscurity, illuminated only by the purest light
in the universe.
In 2005 the Nobel Prize in physics was awarded to Glauber, Hall, and Hensch†† for laser optics and metrology.
†
K. M. Evenson, J.S. Wells, F.R. Peterson, B.L. Danielson, G.W. Day, R.L. Barger
and J.L. Hall,
Phys. Rev. Letters 29, 1346(1972).
††
The
Nobel Prize in Physics, 2005. http://nobelprize.org/

Kenneth M.
Evenson – 1932-2002
[i] A. Einstein, Annalen
der Physik 17,891(1905). (Translation by W. Perrett and G.B. Jeffery, The Principle of Relativity(with notes by A. Sommerfield) (Methuen,
London 1923), (republished by Dover, London 1952).
[ii] W. G. Harter, J. Mol.
Spectrosc. 210, 166(2001).
[iii] W. G. Harter, J. Evans,
R. Vega, and S. Wilson, Am. J. Phys. 53, 671(1985).
[iv] W.G. Harter and T. C.
Reimer, //www.uark.edu/ua/pirelli/html/poincare_inv_2.htm
[v] D. E. Herschbach,
(unpublished, 2005).
[vi] H. Minkowski, Mathematisch-Physikalische Klasse,
vol. 1, 53 (1908).
[vii] H. A. Lorentz
Koninklijke Akademie vanWetenschappen te Amsterdam. Section of Science. Proc.
6: 809-831 (1904).
[viii] Albert Einstein "Zur Elektrodynamik bewegter Korper." Annalen der Physik
18,639 (1905); Annalen der Physik 17,891(1905). (Translation: Perrett and
Jeffery, The Principle of Relativity, (Methuen, London
1923), (Dover, 1952).
[ix] Max Planck "Zur Theorie des Gesetzes der Energieverteilung im
Normal-spectrum."
Deutsche Physikalische Gesellschaft. Verhandlungen 2: 237-245 (1900).
[x] Louis de Broglie,
Nature 112, 540 (1923); Annalen der Physik (10) 2 (1923).
[xi] P. A. M. Dirac, “Forms of Relativistic Dynamics”
Rev. Mod. Physics, 21: 392 (1949).
[xii] Albert Einstein "Uber einen die Erzeugung und Verwandlung des Lichtes
betreffenden heuristischen Gesichtspunkt." Annalen der Physik 17: 132-148 (1905).
(Translation by A.B. Aarons and M.B. Peppard, Am. J. Phys. 33, 367(1965).)
[xiii] E. Schrodinger, Annalen
der Physik (4) 79 361 and 489 (1923); 80, 437 (1926); 81,109 (1926).
[xiv] Schrodinger’s protests about prevailing quantum
mechanical interpretations are widely circulated. So far we have been unable to
locate more solid references.
[xv]
L. C. Epstein, Relativity Visualized. (Insight Press 1981)
[xvi] N. Bohr, Zeitschrift fur Physik,
9, 1-2, (1922).
[xvii] W. Heisenberg, The Physical Principles of the Quantum Theory, (Dover, New York,
1930).
[xviii] P.A.M. Dirac, Lectures on quantum
mechanics, (New York, Belfer
Graduate School of Science, Yeshiva University, 1964). Dirac’s first text in
1931 used á and Č to denote bra-ket duality.
[xix] A. Einstein, "I shall never believe that god plays dice with the
universe" Albert
Einstein Archives, The Jewish National & University Library, The Hebrew
University of Jerusalem (www.albert-einstein.org), Einstein Archives Online,
Volume 15, #294, Letter to Cornelius Lanczos, March 21,
1942,http://www.alberteinstein.info/db/ViewDetails.do?DocumentID=30893.
[xx] R. Feynman, The Pleasure of Finding Things Out, (Perseus Publishing,
Cambridge, MA,1999) p. 8.
[xxi] (unpublished) A huge energy shift is used for sake of geometric clarity.
Atoms usually lose less than one part in 109 or 1010 of
their rest mass in optical emission. The atom in the example loses rest mass
1/2 M2c2
emitting a 3/8 M2c2 photon.
[xxii] R. P. Feynman, R.
Leighton, and M. Sands, The Feynman Lectures (Addison Wesley 1964)
Our development owes a lot to Feynman’s treatment cavity wave dispersion in
Vol. II Ch. 24 and Vol. III Ch. 7.
[xxiii] W. Rindler, Essential Relativity-Special, General, and Cosmological, Springer (New York
1977) p. 18. See also ref. 8, p. 111.
[xxiv] E.F.Taylor and J.A. Wheeler, Spacetime Physics (W. H. Freeman San Francisco 1966) p. 18.
Acknowledgements
The author would like to thank Ronald F. Fox and Eric J. Heller for careful reading and suggestions regarding early versions of this work and Daniel Kennefick for information from the Einstein Centennial bibliography project. Also, we are grateful to Molly Longstreth and Usha Gupta for help with bibliographic search.
Figure Captions
Fig. 1. Comparison of wave archetypes and related axioms of
relativity.
(a) Pulse Wave (PW) peaks locate where
a wave is. Their speed is c for all observers.
(b) Continuous Wave (CW) zeros locate
where it is not. Their speed is c for all colors (or observers.)
Fig. 2. Pulse Wave (PW) as a sum of 12 Fourier CW’s (a) PW
parts: real ReĮ, imaginary ImĮ, and magnitude |Į|.
(b) CW phasor clocks plot real vs.
imaginary parts of wave amplitudeĮ .
Fig. 3. Wave addition of counter propagating Fourier
components.
(a) 2-PW Sum has binary sum has 4
values (0,0), (0,1), (1,0), (1,1) and diamond grid of peak paths on a plane of
zeros.
(b) 2-CW Sum and interference has value
continuum and square grid of zeros.
Fig. 4. “Ficticious” sources and their wave coordinate
lattices in (a) Spacetime and (b) Per-spacetime.
CW lattices of phase-zero and
group-node paths intermesh with PW lattices of “particle” or pulse wave paths.
Fig. 5. Co-propagating laser beams produce a collapsed wave
lattice since all parts have same speed c.
Fig. 6. Laser lab view of 600Thz CW and PW light waves in
per-space-time (a-b) and space-time (c-d).
Fig.7. Atom view of 600Thz CW and PW light waves in
per-spacetime (a-b) and space-time (c-d) boosted to u=3c/5.
Fig. 8. Wave phasor addition. (a) Each phasor in a wave
array is a sum (b) of two component phasors.
(c) In phasor-relative views either A
or else B is fixed. An evolving sum-and-difference rectangle is
inscribed in the (dashed) circle of the
phasor moving relative to the fixed one.
Fig. 9. Doppler shift b-matrix for a linear array of
variously moving receiver-sources.
Fig. 10. (a) Euclidian mean geometry for counter-moving
waves of frequency 1 and 4. (300THz units).
Fig. 10. (b) Geometry for the CW wave
coordinate axes in Fig. 7.
Fig. 11. (a) Horizontal G-hyperbolas for proper frequency
B=v and 2B and vertical P-hyperbolas for proper wavevector k.
(b)
Tangents for G-curves are loci for P-curves, and vice-versa.
Fig. 12. Dispersion hyperbolas for 2-CW
interference (a) Laser lab view. (b)Atom frame view.
Fig. 13. Geometry of contact
transformation between relativistic (a) Hamiltonian (b) Lagrangian.
Fig. 14. “True” paths carry extreme
phase and fastest phase clocks. Light-cone has only stopped clocks.
Fig. 15. Quantum waves interfere
constructively on “True” path but mostly cancel elsewhere.
Fig. 16. Trigonometric geometry (a)
Unit circular area ö=0.86. (b) Unit hyperbolic area Ė=0.99.
Fig. 17. Relativistic wave mechanics
geometry. (a) Overview. (b) Details of contact transform tangents.
Fig. 18. Monochromatic (1-frequency) 2-CW wave space-time
patterns.
Fig. 19. Dichromatic (2-frequency) 2-CW wave space-time
patterns.
Fig. 20. (a-g) Elliptic polarization ellipses relate to
galloping waves in Fig. 18. (h-i) Kepler anomalies.
Fig. 21. Cavity 2-CW modes. (a) Invariant “mass” hyperbolas.
(b) COM frame. (c) ISOC frame.
Fig. 22. Optical cavity energy hyperbolas for mode number
n=1-3 and photon number Nn=0, 1, 2,....
Fig. 23. Simulated spacetime photon counts for coherent
(a-c) and photon-number states (d).
Fig. 24. Optical cavity model of (a) Emission, (b)
Absorption, and (c) Compton scattering
Fig. 25. Compton scattering. (a) Vector sums on mass
hyperbolas of low Ěl , medium Ěm , and high Ěh.
(b-c) Feynman graphs. (d) Center of
Momentum (COM) vector sums. (e-f) COM Feynman graphs.
Fig. 26. Compton nets are congruent Compton staircases of
transitions. (a) f=2:1 (b) f=√2 :1.
Fig. 27. Optical wave frames by red-and-blue-chirped lasers
(a)Varying acceleration (b)Constant g.
Fig. 28. Accelerated reference frames and their trajectories
painted by eĪĖ-chirped
coherent light.
Fig. 29. Dirac matter-antimatter dispersion relations and
diagrams of pair-creation-destruction processes.