Chapter 2. Velocity and momentum

Recall the car-crash problems discussed first in Chapter 1 regarding Fig. 1.1. The first one involves a text-messaging driver of 4-ton SUV going 60mph SUV rear-ending a dawdling 1-ton VW going 10mph. (Fig. 1.1b.) What final velocity or velocities do the cars have? You may have been taught to analyze collisions by solving momentum and energy formulas in a resulting quadratic equation. Fig. 2.1 shows an easier geometric solution using a single line on graph paper. Moreover, its logic is clear enough to derive those formulas!

            As sketched in Fig. 1.1b, the answer depends on whether it’s“Ka-Runch” or “Ka-Bong” or some more generic noise like “Ka-whump”. By“Ka-Runch” we mean the cars crumpled enough to become crunched into one hunk of metal weighing 5 tons. (4+1=5) This is a simple problem that is solved by drawing a line of slope (–4/1) on a velocity vs. velocity graph from before-crash-point  to where that line intersects the red 45° (V_SUV=V_VW)-line at the after-crash-point (Fig. 2.1)

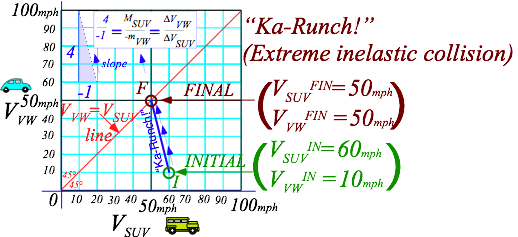
Fig. 2.1 Anatomy in velocity space of a “Ka-runch!” that is an extreme inelastic collision.

            The logic behind a (V_SUV=V_VW)-line is that crunched vehicles have equal velocity. The logic behind a Ka-Runch-line of slope (–4/1) is subtler. It is due to Newton’s 1^st axiom or “law” that says Nature conserves so-called momentum, a sum of products of each mass with its velocity. It’s a law we can live with but, why?

Momentum exchange: a zero-sum game

During the car crash the velocity coordinate pair (V_SUV ,V_VW) change very rapidly in moving from initial point I at (60,10) to final point F at (50,50) in Fig. 2.1. The Ka-Runch takes less than a second. In that time, SUV is losing only one unit of velocity for every four units gained by VW since SUV is four times heavier than VW.  Newton writes this as a total momentum conservation equation.

                        P_SUV +P_VW =M_SUV·V_SUV+ m_VW·V_VW = P_Total =constant                       (2.1)

Checking (2.1) with Fig. 2.1 gives a total momentum P_Total =250 that SUV and VW have together.

            4·60+1·10 =4·V_SUV+1·V_VW =4·50+1·10 = P_Total =250                                   (2.2)

The change of P_Total must be zero (ÄP_Total =0) before, during, and after the crash. It’s a zero-sum game.

                                    M_SUV·ÄV_SUV+ m_VW·ÄV_VW = ÄP_Total =0                                              (2.3)

Dividing by SUV change-of-velocity (ÄV_SUV) and VW mass (m_VW) gives the slope relation in Fig. 2.1.

                                                  or:                                                    (2.4)

           P_Total is also conserved in an ideal Ka-Bong of Fig. 2.2. Here cars bounce off each other without damage. That’s unlikely at 60mph speeds! So Fig. 2.2 is rescaled to units of feet per minute. Then initial =60 feet per minute=1ft. per sec. is more like a parking lot speed. (Insurance claims are a lot less!) The VW is bumped from an initial =10 ft per min to =90 ft per min=1.5 fps=1.02 mph. To find in Fig. 2.2, draw an arc from initial I-pt (60,10) to hit final F-pt (40,90). Arc-center is Center of Momentum COM pt-(50,50) on the 45° line. (It’s the final point if cars get “stuck” to each other as in a Ka-Runch like Fig. 2.1.)

 Fig. 2.2 Anatomy in velocity space of a “Ka-Bong!” that is an extreme or ideal elastic collision.

The Ka-Bong in Fig. 2.2 is like the Ka-Runch in Fig. 2.1 followed by an equal but opposite rebound or hcnuR-aK (un-crash) that undoes the “damage” by the Ka-Runch. Now you might ask, “Is this possible outside of the cartoon world or a video game?” Well, certainly not at high speeds and not quite at low speeds.

 Only in a quantum nano-world do perfectly elastic processes exist. Any classical collision, however gentle, is audible, visible, and disturbs or exchanges many atoms, electrons, and photons. This is called “wear&tear” or entropy growth. (Usually one ignores it until it has gone too far. Then it fills landfills!)

Even gentle bumps like the one starting at initial pt-I in Fig. 2.2 cannot quite go exactly to final pt-F on the COM circle, but collisions with no appreciable damage pass as (almost) elastic or time reversible bumps. A video of the Fig. 2.2 IF bump played backwards looks like an FI bump that is quite ordinary. But reversed video of the Fig. 2.1 crash looks like a crazy “un-crash” as ruined cars get reborn like new.

Deducing (perfect?) conservation from (ideal?) symmetry

Newton’s momentum or P-conservation axiom or “law” is one of the most strictly enforced laws in classical physics. (It’s also quasi-conserved in quantum physics that so often seems to get away with utter mayhem!) Momentum is like some kind of fluid that you might buy and sell but cannot create or destroy. In our car bumps or crashes the zero-sum-rule says, “Whatever P the VW gains (or loses) the SUV loses (or gains.)”

A classical law without classical proof remains an axiom until deeper theory may rule on it. Quantum theory has ruled and can shed some light on origin and properties of this mysterious “P-fluid.” It also shows how to cheat P-conservation and other classical “laws” a little. This will be discussed in later units.

In the meantime it is possible to relate P-conservation to more fundamental axioms that are called symmetry principles. Symmetry is a grown-up geometry that is also very useful in the quantum world. Most immediately, symmetry helps deduce principles of energy E and E-conservation as discussed below.

Symmetry means “same-etry” or “similarity” or “smoothness” and other “s” words like simplicity. One fancy technical term is isotropy or isometry with iso meaning same. For example, the most symmetric ball would be a sphere that is isotropic by having the same radius everywhere. A most-isotropic (or most-symmetric plane) is flat and bump-free. Some would say symmetry means Beauty, but others might say it means Boring. Think of a seemingly endless Kansas prairie for either response.

Symmetry can refer to sameness in time as well as in space and often the two are related. (Think of driving across Kansas.) The idea of being time reversible is an example from the preceding page. Another is Galileo’s relative-velocity symmetry or Galilean relativity. Both are involved in Fig. 2.2 and Fig. 2.4 below.

Galilean time-reversal symmetry

Suppose a traffic cop is going 50mph in a lane adjacent to the one occupied by the SUV and VW. He or she records (using radar) the SUV coming up at 60mph, and puts on the blue-light to stop it for exceeding the 20mph limit in a school zone. Then Ka-Runch! as SUV+VW become a single 5-ton hunk going 50 mph, the same speed as the cop. (The cop can just reach across to hand SUV a cyber-ticket for (1) speeding in a school zone, (2) improper following, and (3) driving while faxing. c-tickets are costly even for rich SUV-ites!)

            The V_VW vs. V_SUV graph for the Ka-Runch is shown in Fig. 2.3 as viewed by the 50mph cop. It is the same as Earth-frame-view in Fig. 2.1 except the cop’s speed of 50mph is subtracted from both V-scales. The cop sees a final 5-ton SUV-VW hunk going 0 mph relative to cop-frame or COM frame of SUV+VW.

            The V_VW vs. V_SUV graph for the Ka-Bong in Fig. 2.4 is also viewed in the 50mph cop-frame or COM-frame. Again, it’s just Fig. 2.2 with 50mph subtracted off V-scales. Cop or COM-frame view shows simplicity and symmetry. Velocity values simply change sign as the Ka-Bong crosses the whole COM-circle diameter.

Initial I-pt (10,-40)  (reflection thru COM pt-(0,0))  final F-pt (-10,40)

Reversing time  makes (-)velocity  and reflects I-pt and F-pt into each other.

Initial I-pt (-10,40)  (reflection thru COM pt-(-0,-0))  final F-pt (10,-40)

That is just Fig. 2.4 with blue time-direction arrows reversed. (INITIAL I switches places with FINAL F.)

            Elastic collisions (Fig. 2.4) are symmetric and balanced to t-reversal, but inelastic Ka-whump’s are unbalanced if they stop short of the COM circle. A Ka-Runch (Fig. 2.3) is unbalanced to the extreme.

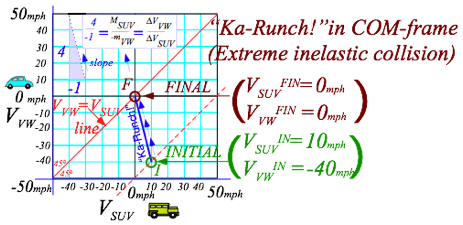
Fig. 2.3 COM-frame or 50mph cop-frame view of a “Ka-runch” inelastic collision of Fig. 2.1.

Fig. 2.4 COM-frame or 50mph cop-frame view of a “KaBong” elastic collision of Fig. 2.2.

            This is a common situation in physics. The real (or generic) world lies between extreme ideals that are easiest to quantify. On one hand, we’ll say a Ka-whump that ends up close to its inital COM-circle is elastic or Ka-Bong-like and, on the other hand, a Ka-whump that stops near its COM-point is inelastic or Ka-Runch-like.

Galilean relativity and spacetime symmetry

Galileo grew up in Renaissance Italy as it flourished from its sea trade. Perhaps, watching ships of trade glide smoothly in the harbor led him to ideas about relativity of velocity. In any case he wrote about comparing what a sailor sees in a ship-frame with what is seen in the Earth-frame. He noted how apparent velocity of an object decreases by subtracting the velocity of the observer’s frame.

            Subtraction of the cop’s velocity V_cop=50 from Earth-frame velocity (V_SUV,V_VW)=(60,10) of SUV and VW in Fig. 2.2 gives their initial velocity (60,10)-(50,50)=(10,-40) in cop-frame. (Fig. 2.4) Such a subtraction (or addition if the cop goes the other way) is a Galilean relativity transformation. Fig. 2.4 is a redrawing of Fig. 2.2 with new (V_SUV,V_VW) scales, each reduced by 50mph. Or else, start with Fig. 2.2 and slide each velocity point down 45°-line by 50mph, (COM /cop-frame Earth-relative velocity) as in Fig. 2.5a.

It is a kind of “slide-rule” in Fig. 2.5b that quantifies several Galilean frames. The initial VW frame (VW(I)) is found where the 45°-I-line hits the horizontal (V_VW=0) axis. VW starts in frame-VW(I) and is hit by a (V_SUV=50)-SUV that knocks VW into a new frame-VW(F) of final V_VW=80 as SUV slows to a final V_SUV=30.

Next a final SUV frame (SUV(F)) intersects the 45°-F-line on the vertical (V_SUV=0) axis where a final point-F_SUV(F) (V_SUV,V_VW)=(0,50) results if initially a (V_SUV=20)-SUV Ka-Bongs a (V_VW=-30)-VW at point-I_SUV(F).

            Note that seven Ka-Bong lines in Fig. 2.5 show seven different-frame views of the same Ka-Bong. In four frames, one car has V=0 either before or after the Ka-Bong. One frame, the COM has V_COM =0 before and after. That COM-frame is balanced to velocity reversal . Other frames have distinct V-reversed twins with INITIAL I and FINAL F switched, such as symmetry twins I_SUV(F)F_SUV(I) and F_SUV(F)I_SUV(I) on each side of the central COM-frame in Fig. 2.5b.

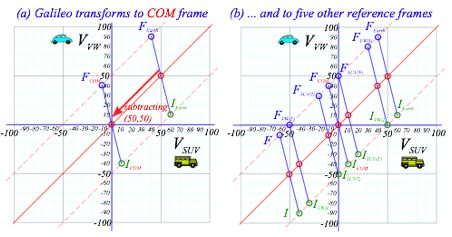
Fig. 2.5 Galilean transform of  “KaBong” in Fig. 2.2 to (a) COM-frame and (b) to other frame views.

Geometry of Balance: Center of Momentum (COM) and Center of Gravity (COG)

The uniqueness and constancy of a COM for the SUV and VW is connected with underlying space-time symmetry or geometry of spatial balance in Newton’s equation (2.1) repeated here in different forms.

                        P_Total =P_SUV +P_VW =M_SUV·V_SUV+ m_VW·V_VW = M_TOTAL·V_COM=constant                        (2.5a)

Total momentum is a product of V_COM and total mass M_TOTAL=M_SUV+m_VW of a 5-ton SUV-VW “hunk”. This holds whether the “hunk” forms permanently in a Ka-Runch or the cars bounce off in a Ka-Bong or Ka-whump. Both P_Total =M_TOTAL·V_COM and V_COM are constant throughout the collision regardless of “auto-elasticity.”

                                                                  (2.5b)

Weighted average V_COM of (V_SUV,V_VW) is fixed as V go from initial to in-between to final values. Collisions in Fig. 2.1 thru Fig. 2.5 all have V_COM=50 in the Earth frame. The 4:1-weighted average of each coordinate pair (40,90), (50,50), (60,10), (70,-30),etc. on the slope-(-1:4)-line (in Fig. 2.6a below) is V_COM=50.

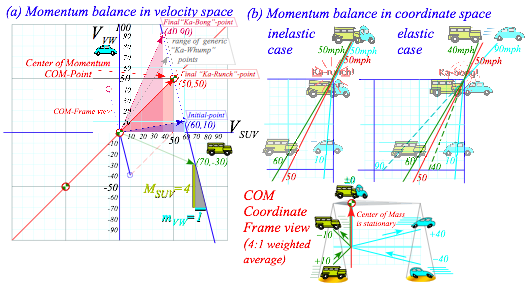
Fig. 2.6 Geometry of (a) 4:1-weighted velocity average (b) 4:1-weighted coordinate average.

            Balance between velocity V_SUV and V_VW in (2.5b) relates to balance between position x_SUV and x_VW.

                                                                                  (2.5c)

As SUV and VW close, collide, bounce, or stick, the Center of Mass x_COM stays at a constant velocity V_COM. In the COM frame that velocity is zero as sketched in the lower part of Fig. 2.6b. The weighted average x_COM in (2.5c) of coordinates x_SUV and x_VW is also a Center of Gravity and is cartooned by a 4:1 Greek balance.

Exercise 1.2.1

Redraw Fig. 2.5 for initial speeds (V_SUV=40,V_VW=10) with the SUV only twice the mass of the VW. (Hummer-Lite) Include also a line describing the frame in which the SUV is initially stationary and another for which the SUV is finally stationary.