Introduction to Text
Page in Text
Preface: Three Quakes for Physics 4
Pillars of Modern Physics: Special relativity (SR) and Quantum Mechanics (QM)
Thumbnail sketches of Unit topics 6
The weapons of math instruction 10
About the computer simulations: LearnIt and CodeIt 12
About Logic: Some philosophy concerning axioms 13
Preface: Three Quakes for Physics
The history of physics has seen three major developments, so far. In hindsight each is like an earthquake and tsunami with decades of aftershocks that forever alter intellectual and philosophical culture beyond the insular confines of our relatively tiny physics community. Very roughly Quake-1 is classical physics, Quake-2 is modern physics, and Quake-3 is postmodern physics,
Quake-1, classical physics begins with the mechanics of Galileo (1564-1642), Newton (1642-1727), Lagrange (1736-1813), Hamilton (1805-1865) and the electromagnetism of Faraday (1791-1867) and Maxwell (1831-1879). (Just a few main pioneers are being listed.) Quake-1 aftershocks relatively quickly overthrow many paradigms of Aristotle (384-322 BCE) that held for centuries and open up three fields of engineering, mechanical, chemical-thermal, and electrical.
Quake-2, modern physics begins in
1900 with a foreshock known as
the quantum axiom
![]() of Planck (1858–1947) in a theory of low-T light. Planck feared he had goofed and tried to recant. (More on this in Unit
2.) The main shock soon follows with the explosion of annus mirablis 1905 with five papers by
Einstein (1879-1955) introducing the special theory of relativity, a theory of quantum photoelectric
effects, relativistic mechanics, and a statistical theory of molecular
collision dynamics (Brownian motion).
of Planck (1858–1947) in a theory of low-T light. Planck feared he had goofed and tried to recant. (More on this in Unit
2.) The main shock soon follows with the explosion of annus mirablis 1905 with five papers by
Einstein (1879-1955) introducing the special theory of relativity, a theory of quantum photoelectric
effects, relativistic mechanics, and a statistical theory of molecular
collision dynamics (Brownian motion).
Quake-2 leads to decades more of aftershocks as many theorists and experimentalists discover one extraordinary effect after another. These will open dozens of new branches of physics and engineering. Branches of American Institute of Physics (AIP) or American Physical Society (APS) introduced in this text include Atomic-Molecular-Optical (AMO), Chemical Physics (CP), and Condensed Matter (CM). These areas can often “see” their effects with coherent (laser) light or quasi-coherent (synchrotron) light beams while experiments in Nuclear Physics (NP), Magnetohydrodynamics (MHD) and High Energy Physics (HEP) generally involve particle beams that are incoherent but with energies that are million, billion, or trillion times greater than typical AMO experiments. The text starts with coherent lower energy AMO phenomena having the greatest precision, clearest theory, as well as the coolest applications.
However, Quake-2 has one more aftershock due to Einstein and this one involves higher energies than all the others put together. His 1915 paper on the general relativity (GR) theory for gravity opens the fields of astrophysics and cosmology. His prediction for the bending of light by our sun and explanation of Mercury’s orbital precession were results that brought more world attention to physics and a physicist than ever before or since. Recently modern astronomical observation using the NASA Hubble and Spitzer orbiting scopes and spectrometers, COBE data, and coherent optical ground arrays yield extraordinarily clear views of GR physics in an enormous universe going back nearly 14 billion years to the Big-Bang.
These show a zoo of colossally beautiful objects and processes that are beyond anything one would have imagined and more are being found practically every day.
Quake-3, postmodern physics begins around 1970 with developments known variously as string-theory, super-symmetry, brane-theory, and Theory-of-Everything (TOE). Quake-3 has a problem. As of 2011 virtually no experimental evidence exists for it. As Nobelist Sheldon Glashow put it, “You can do string theory or you can do physics. But, you cannot do both.”
This TOE hopes to be a “grand unification theory” (GUT) that upgrades classical GR theory of our weakest force, gravity, to give a “quantum gravity” (QG) theory. The hope is to combine QG with existing quantum theories of weak nuclear (WN) forces and stronger quantum-electro-dynamic (QED) forces (QED and WN combine after a fashion into an “electro-weak”(EW) “gauge theory.”) and finally with strongest quantum-chromo-dynamic (QCD) baryonic forces. A combination of EW and QCD field theories is named “The Standard Model” (TSM). String theorists argue, with some justification, that TSM is a kluge and hope to improve upon TSM by adding gravity to the mix by combing QG with TSM (or some improved mix of EW and QCD) to make a TOE. However, a QG theory that is experimentally predictive has yet to appear.
So the Quake-3 situation appears more like a raging volcano than a series of sharp quakes. So, you may excuse me for leaving you with references[1],[2] describing the TOE efforts (Included are one that seems to 6warn, “Stay away!”) and deal mainly with currently reliable and verifiable physics.
Pillars of Modern Physics: SR and QM
The text will try to show a clearer view of the two fundamental Quake-2 theories that do have compelling corroboratory evidence. These two pillars of current modern (and most postmodern) physics are special relativity (SR) and quantum mechanics (QM). SR and QM were first combined by Dirac (1902-1984). Later this was extended by Feynman (1918-1988) to give the QED theory for which he shared the 1965 Physics Nobel Prize with Schwinger and Tomonaga. Use of SR and QM to understand AMO, CP, and CM phenomena yields extraordinarily useful devices such as lasers, optical quantum wells, cheap powerful computers, global positioning systems (GPS requires GR, too!), magnetic resonance imaging (MRI), Bose-Einstein Condensates (BEC), and high resolution spectroscopy (HRS) just to name a few of the topics to be introduced in this text.
It happens that SR and QM are actually quite full of mysterious properties in spite of their rock-solid experimental verification and multitudinous day-to-day applications. This is painfully obvious to many who take (or teach) either one. A common after-course student evaluation for either SR or QM is, “I didn’t understand this subject but then neither did the prof!” Interestingly, it happens that the more painful parts of either course are at the beginning where axioms get laid out. There the instructor must stammer, “OK, this sounds crazy. But, trust me! It all works out in the end.” Then it does. Sort of.
Now there is a famous approach to QM that many regard as a breath of fresh air for that subject. It involves my first graduate advisor Dick Feynman at Cal Tech. In the early 1960‘s he lectured and cowrote the Feynman Lectures on Physics Vol 3 (Addison Wesley 1964) with Matt Sands and Bob Leighton. That book takes a uniquely insightful and wonderfully unconventional approach to QM that taught me more than any other expositions I had seen. His SR approach is more conventional, but his GR text Feynman Lectures on Gravitation (Persius 1995) coauthored with Fernando Morinigo and Bill Wagner (my second and final graduate advisor) is a wonderful approach to GR, a subject that is still very much a work in progress.
Thumbnail sketches of Unit topics
The approach to this text is in the spirit or modus
operandi by Feynman et. al. while seeking to add to it. It begins
with a uniquely modern review of classical axioms and theory of Galileo,
Newton, Lagrange, Legendre, Hamilton, and Poincare in Unit 1. What’s new here
is very very old. Each part is developed first by using ruler and
compass plane geometry of Thales (~600 BCE) and Euclid (~300 BCE) on graph paper, then analytic geometry
of Descartes (1596-1650),
and finally by Newtonian calculus and “grown-up geometry” now known as symmetry analysis or group algebra. 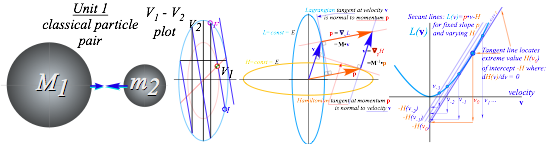
Unit 1 physics is derived almost entirely by Mac computer-aided thought experiments involving collisions between pairs of “superballs.” (More about “computer-aided” below. Both Greek and silicon computers play a role.) The geometry (excerpts above) is quite powerful. It leads directly to the theories of Galileo, et. al. and is ready to be upgraded to SR and QM in Unit 2, that is, to the theories of Einstein, et. al.
Unit 2 starts as a uniquely modern review of Einstein-Poincare special relativity theory that is also developed first by Thales-Euclid axiomatics. What’s new here is a simple and unifying picture revealing SR and QM as inseparable parts of the same subject. Separate treatments of SR and QM contain mysterious axioms and results. Many of these mysteries vanish if the two are developed together geometrically. The resulting symmetry algebra is also simpler and more accessible. It is probably not an exaggeration to say that relativistic mechanics (which is a revealing upgrade of classical mechanics) is derivable by six easy ruler-and-compass steps. (Cover design displays one view of this.) Feynman’s Six Easy Pieces (Persius 1997) should have included this. But, he had no Mac to reveal subtle wave effects that make this work!

Unit 2 physics was first
derived using computer aided thought experiments involving collisions between
pairs of Continuous Wave (CW) lasers. (The common acronym CW also stands
for Colored Wave, Coherent Wave, and Cosine Wave, each
representing important principles.) Both SR and QM are theories about light
waves. A careful study of CW wave interference leads to extraordinarily simple
axioms and formulation for both. That a theory of massive matter should arise
from one involving zero mass “matter” is surprising. But, it is supported by an
experimental result; the electron pair production due to ![]() -pairs found
by Carl Anderson (1905-1991).
(Carl introduced me to Feynman when I interviewed for graduate admission.)
Feynman diagrams of this still amazing process are sketched below and
introduced in Unit 2.
-pairs found
by Carl Anderson (1905-1991).
(Carl introduced me to Feynman when I interviewed for graduate admission.)
Feynman diagrams of this still amazing process are sketched below and
introduced in Unit 2.

Unit 3 returns to review classical foundations with the study of resonance, the single most important process in all of Nature and key to most applications of science, technology, and mathematics. Without it we are all deaf, dumb, and blind. Again, this is a theory based on relative geometry of pairs, first and foremost, a pair of coupled pendulums or forced damped oscillators sketched in excerpts below.
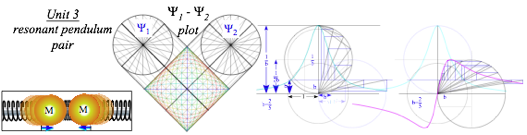
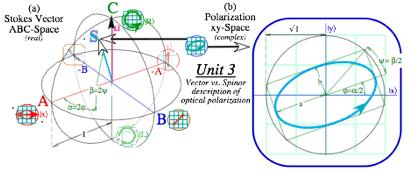
This classical theory is directly and precisely analogous to the equations of motion for quantum mechanics, spectroscopy, and to the theory of optical polarization, a powerful tool in modern physics and astrophysics. It started in 1867 with Stokes’ optical “spin” vector and Poincare space sketched below. We revive this to make a useful analog to quantum spinor theory of electron or nucleon polarization that came along 60 years later.
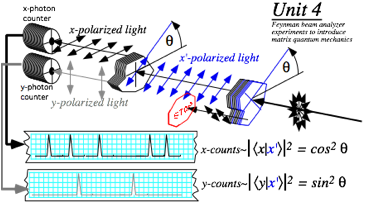
Unit 4 uses optical polarization analogies to develop quantum measurement phenomena following Feynman’s beam analyzer thought experiments sketched below. This includes theory behind 2-state dynamics of laser transitions, electron spin resonance (ESR), nuclear magnetic resonance (NMR) or magnetic resonance imaging (MRI) and other spin resonance phenomena in the kHz-GHz spectral range.
Unit 5 develops the Fourier analysis and symmetry algebra that is a powerful approach to theory of n-state quantum systems, again with classical analogies and foundations. This includes molecular orbital wave states and quantum dynamics of quantum-well or nano-dot structures sketched below.
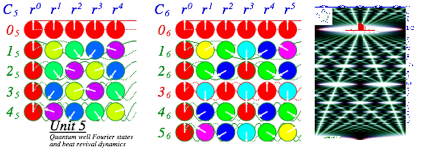
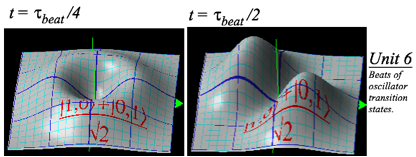
Unit 6 develops the quantum oscillator in one and two dimensions using modern algebraic tricks that simplify the derivation and application of number states and coherent states wave-functions. This is applied to quantum optical and molecular vibrational phenomena in the GHz-THz spectral range. The excerpt below is the quantum correspondent to the resonance described in Unit 3 excerpt.
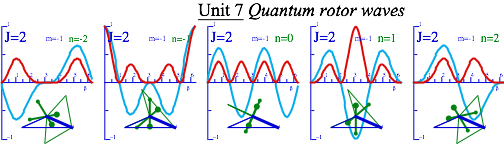
Unit 7 develops the quantum orbital states and molecular rotational wavefunctions in two and three dimensions using a combination of Unit 4 and Unit 5 topics. This is applied to atomic and molecular electronic transitions in the THz to PHz spectral range. Excerpt below is a new way to view these waves.
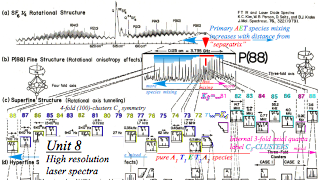
Unit 8 will deal with current research topics such as high resolution laser spectroscopic effects.
The modern physics world is
enormous and growing. We will barely scratch its surface in this text.
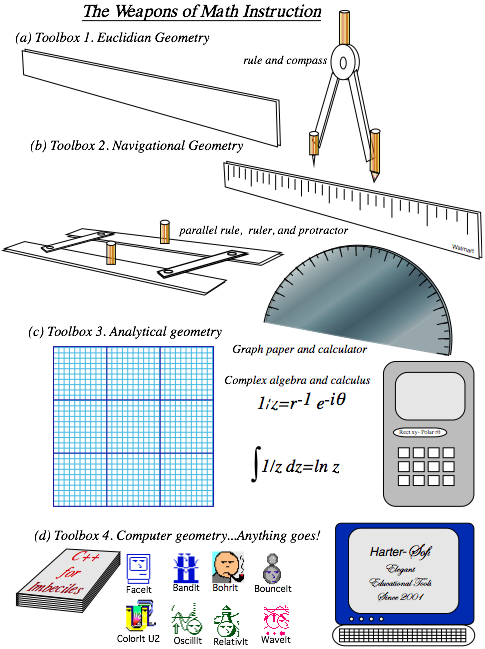
The weapons of math instruction
When your physics fails (as in String theory) it could be you have lousy axioms. If so, it’s back to the drawing board. That’s how we start this course. It goes wa-aaay back to geometry of Thales (600BCE) and Euclid (300BCE). You should always ask what tools have survived the test of time and check them out.
Toolbox 1: Euclidian plane geometry (Rule and compass)
Note that Toolbox 1 has a rule not the ruler. That’s in Toolbox 2. A rule is just a straightedge, a ruler without its inch or mm scale. Euclid’s pretty strict about this. Formal plane geometry is kind of a game to see how much you can do drawing lines and circles with just these tools. And a pencil…did I forget the eraser?
Toolbox 1 has limitations, at least by formal rules of Mr. Euclid. You may have heard that you can’t trisect an angle as Mr. Euclid wants it done, formally and exactly in a finite number of steps. That won’t stop us. We’ll do that and other “illegal” moves approximately and in as few steps as possible using tools below.
Toolbox 2: Navigational geometry (Set 1+ protractor, ruler, divider, parallel rule)
These were the tools used by the Portuguese, Spanish, Dutch, French, and English navigators who were at least indirectly responsible for many of us living in the American continent. These tools were also used by weekend sailors until the Global Positioning System made obsolete all but six-packs of beer.
Toolbox 3: Analytic geometry (Set 2+ graph paper, algebra, calculus, calculator)
The idea is not to discard algebra and other such formalisms but to understand them better. So one of the first things we do with each geometric graph is figure it out using algebra. This is called analytic geometry and is one of the quickest ways to understand calculus and its application to physics. This leads to complex algebra and geometry that is very important to physics. As a crutch for the arithmetically and algebraically challenged we include scientific calculators. (Most of these have complex algebra capability.)
Toolbox 4: Computer geometry (Set 3+ high resolution graphics, C++ etc.)
This is the “open” class of geometric analysis, and anything goes. A modern scientist without graphics programming is at a disadvantage. Current languages of greatest general usage, speed, and power are C++ and Objective C used to write simulations BounceIt, BandIt, etc. for this book. High-level languages such as Maple™, Mathematica™ are fine, too. But, by being jacks-of-all-trades they can become masters-of-few.
This is challenging stuff. Doing it will seem hard sometimes. Rome was not built in a day and neither was any understanding of Nature. So this book depends most on how much you like thinking and doing.
Ignorance about science is not a burden you must accept. It is a challenge you should overcome.
About the computer simulations: LearnIt and CodeIt
The first tier of computer programs in this book is the LearnIt series consisting of BounceIt, OscillIt, QuantIt, WaveIt, etc. listed in the table below. These are (hopefully) user-friendly applications that made many of the figures in this book and provide animated visualizations of physical phenomena or analogies thereof. They are analog computers that allow text figures to become dynamic thought experiments.
The suffix “It” attached to most of these programs is derived from the FaceIt interface invented by Dan Kampemier, founder of FaceWare in Urbana, IL, one of the first worldwide programming projects. I participated in FaceWare from 1985 until 1993 and am now involved in its re-application in Apple’s X-Code and IOS. Advantages of FaceWare or X-Code is its graphical user/programmer interface (GUI or GPI) that can be easily updated with new menus, dials, text editors, spreadsheets, OpenGL windows, etc.
Another advantage for academic application is that good GPI’s keep model, control, and view separate. This avoids time wasted reinventing the wheel or debugging buttons in class. Now teaching useful root-level object oriented programming along with physics is possible. Mixing serious academics with deep coding is still regarded as heresy, but sooner or later it should be more a part of serious science education.
GPI’s facilitate a tree of programming projects for a given course. Such project trees make up a CodeIt system. Students learn how to saw-off one or more branches of CodeIt trees to build their own applications as homework or lab projects. Eventually, they can build applications of sufficient complexity to aid in their thesis or dissertation research projects. Also, select CodeIt applications may be added to the LearnIt collection, a way for a student to first “publish” his or her best work. Each LearnIt program is supposed to have an accompanying expository text and/or on-line help hypertext.
Listed below are Units 1-8 with some LearnIt and CodeIt programs that apply to each.
Unit 1 Review of elementary mechanics of velocity, momentum, energy, and fields.
Collisions: BounceIt, Fields: AnalyIt, Oscillation: BoxIt and ColorU(2), Orbits: CoulIt .
Lagrange and Hamiltonian mechanics : TrebuchIt with help from Pendulum and Cyclotron.
Unit 2 Relativity and quantum wave mechanics
WaveIt, BohrIt, RelativIt (Ongoing development includes site:
https://www.uark.edu/ua/pirelli/php/title_page.php or: https://www.uark.edu/ua/pirelli/php/pirelli_trail_map.php )
Unit 3 Resonance, oscillation, and waves.
OscillIt , WaveIt, ColorU(2), JerkIt, and BoxIt with help from CnvMolVibes.
Unit 4 Feynman beam analyzer approach to quantum operator theory
QuantIt and AnalyIt with help from ColorU(2).
Unit 5 Fourier analysis, quantum Hamiltonian, and time evolution.
WaveIt, BohrIt. (Others under development.)
Unit 6 Quantum oscillators.
BohrIt, ColorU(2) and CoulIt with help from CnvMolVibes. (Others under development.)
Unit 7 Quantum rotors and orbitals
QuantIt, ColorU(2) and CoulIt
Unit 8 AMO Research topics (Under development.)
About Logic: Some philosophy concerning axioms
This book is a geometric approach to classical mechanics. By geometry we mean both the Greek and German kind, that is, both the plane geometry of Euclid (~300BC) and the differential geometry of Gauss and Riemann (1800-1900). We begin with ruler&compass constructions of collision mechanics and potentials. Geometry helps clarify the logic of calculus and physics of mechanics and show the symmetry principles behind classical theory that underlie quantum theory. Then we we’ll do relativity and QM the same way.
From the earliest Euclidean geometry through modern mathematics and physics we encounter axioms at the very beginning of each development. These are a priori assumptions that underlie all subsequent logical development. Logic relies on the axiom set. We hope to produce maximum truth, that is, ideas that will longest survive the test of time and experiment. We need to choose the best axioms to do that. But, how?
To parse this let us consider two extremes each written by a friar (churchman) who sought truth during the 1300-1400 late medieval period when there was precious little. On one hand we have William of Ockham (~1285-1349) now known for Occam’s razor. He wrote, “Pluralitas non est ponenda sineneccesitate” trans:
(Plurality should not be assumed without necessity). The other is Martin Luther who wrote the following in The Lies of the Jew (1433). “Die verfluchte hure, vernunft.” trans: (That damned whore, reason.)
Martin was angry at Jews who refused to convert to his axiom set. He was also angry at Copernicus who was proposing a non-geocentric solar system that he thought contradicted his scriptural axiom set.
“The fool wants to turn the whole art of astronomy upside-down. However, as Holy Scripture(Joshua 10:10-15.) tells us, so did Joshua bid the sun to stand still and not the earth.....’’(Copernicus is)... "a fool who went against Holy Writ"
So whose axiom set produced the most lasting truths?
Here we are comparing two parts of human neurophysiological anatomy, the cerebral cortex (CC) and the lower limbic lobes (LLL) that include what we call reptilian “lizard-brain” and mammalian “ rat-brain” lobes. For most of history, humans are totally LLL-dependent. It’s our evolutionary residual unconscious operating system (Human DOS 1.0). LLL “boots-up from the box” while CC requires difficult education.
Humans attempts to develop the CC are so sporadic at first it is impossible to label its emergence. Traditionally one points to the Seven Liberal Arts as our break with pre-medieval superstition. The seven consisted of the Trivium: (Grammar, Logic, and Rhetoric), and the Quadrivium: (Arithmetic, Geometry, Astronomy, and Music). The term Liberal is interchangeable with Liberating and probably was used to designate a pathway to avoid slavery. It appears that the Trivium contains drivers of the creative results in the Quadrivium. Indeed the latter has grown to more like Seven Thousand Liberal Arts and Sciences in just a few centuries. It’s an explosion! You’ll have to excuse physics and chemistry for not making the first cut. Those alchemists were busy distilling gold from horse urine. (Nice try, but a little too stinky for polite liberal company.)
Occam, was a CC user and studied all the ancient texts he could find. (A lot got burned when Bishop Cyril (later a saint) ordered Coptic Christians to destroy the Alexandrian Libraries and brutally murder the famous lady mathematician Hypatia in 415AD. (This is described in Edward Gibbon's "The Decline and Fall of the Roman Empire." Less reliable accounts say Caesar accidentally destroyed the library in 48 BCE.)
Luther, on the other hand, was more anti-scholarly, at least with regard to Copernicus. His LLL attitude was less Seven Liberal Arts and more Seven Deadly Sins. These may also be divided into a Trivium and a Quadrivium, however now the latter (Greed, Envy, Lust, and Gluttony) are drivers of the former (Pride, Wrath, and Sloth), that is, Pride or “Gloating” if your Greed, Envy,..etc. yields success, or else Wrath or “Rage” if you are unsuccessful, followed by Sloth or “Depression.” These are just drives and responses of LLL acquisition processes involving short term ebb and flow of our small 3-to-5-ring molecules called neurotransmitters.
So how creative is the LLL approach of Luther with its enormously complex and rigidly cumbersome axiom set? Can LLL’s claim thousands of new sins? Well, perhaps we can credit modern LLL users (known as the rabid right) with two new sins, namely Torture and Terror that were recently declared quite legal.
However, these two are hardly new. The ancient churches have had them all along. They just did not classify them as sins per se, but rather as “parishioner management.”
In conclusion, let me argue in favor of the Occam Razor approach to logical quests and paraphrase it with the common suggestions “Keep it simple and make it powerful!” or “Assume the least, prove the most.” Occam’s razor is supposed find ways to cut down any axiom set or sine qua non (without which there is nothing). It is amazing that such a “cutting” idea actually works! Perhaps, by reducing logical clutter, we hack away unknowns and clear the way for new stuff. But, there is more to it than that.
Thought driven by a desire to undermine its own premises leads to a thought path that grows geometrically as the CC harnesses the LLL. It’s mind over matter! An exponential explosion of mathematics, science, and technology results. The CC’s “faith” in its axioms must be a temporary one. All logical laws are made to be eventually broken. (Including, presumably this one. Maybe, there is a TOE!)
Of course, Occam’s idea was heresy and he was nearly “fired.” as were Copernicus, Galileo, Bruno, and most other CC pioneers following such thought progressions. (In 1600 Bruno attended a church barbecue where he was the charcoal.) Hacking sacred Churchly axioms or mythos is always trouble. Occam’s idea is to always, “Hack the axioms to save man.” The Church says, “Hack the man to save axioms.” I’ll vote for Occam!
I hope these words (and equations combined with geometry) will serve you creatively.
William G. Harter
Fayetteville, Arkansas
January 2012